安全开发 | 如何让Django框架中的CSRF_Token的值每次请求都不一样

前言

用过Django 进行开发的同学都知道，Django框架天然支持对CSRF攻击的防护，因为其内置了一个名为CsrfViewMiddleware的中间件，其基于Cookie方式的防护原理，相比基于session的方式，更适合目前前后端分离的业务场景，但美中不足的是，其生成的csrf_token在一个session周期中是不变，这对于一些特定的业务场景，显然有点遗憾。

为了弥补这个遗憾，本文介绍一种不用修改CsrfViewMiddleware中间件源码的方式，实现基于请求的csrf_token更新方式，详文如下。

实现过程

1、Django csrf 校验的两个场景

在业务场景中，有两种不同的csrf防护场景，一种是基于Form 表单提交数据的防护，一种是基于ajax 异步请求数据的防护。

对于Form 表单，可以通过在表单中内置`{% csrf_token %}` 实现在提交数据时一起携带csrf_token提交上去，从而通过后端csrf 校验。

这里顺便提下 Django模板引擎是如何渲染`{% csrf_token %}`的，其实就是将`{% csrf_token %}` 替换成csrf_input的返回值（这点可从Django 模板引擎源码中找到），如下：

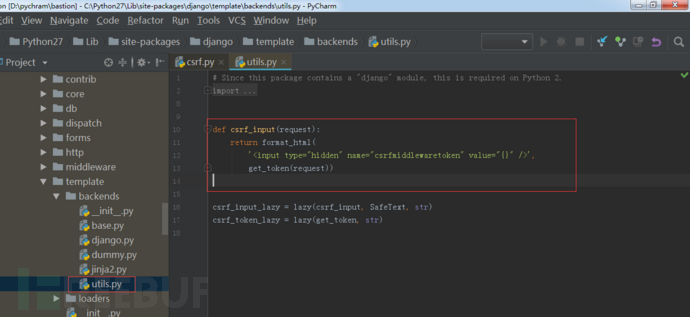
而get_token则是从request.META['CSRF_COOKIE']中获取：

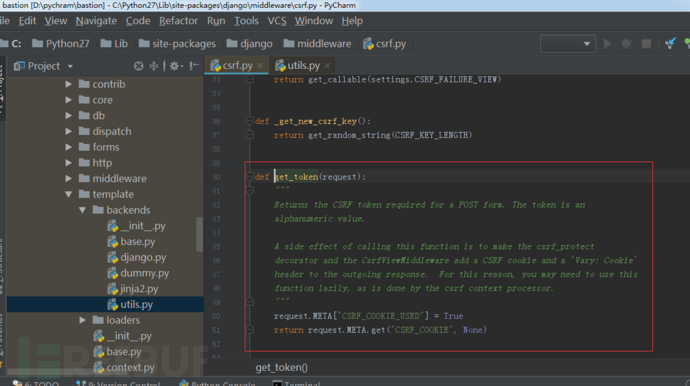
对于ajax 请求，需要在提交请求的时候，添加一个名为x-csrftoken的头部（这个头部是Django源码中内定的），值为从cookie中提取的指定name的值，这个name可自定义，比如下图为`csrf-bastion`：

2、Django csrf token 的生成流程

主要关注下CsrfViewMiddleware 中间件的process_view和process_response。

process_view的主要功能之一就是从请求的cookie中提取指定name的（通过settings.CSRF_COOKIE_NAME指定）cookie值为：csrf token，然后赋值给request.META['CSRF_COOKIE']，如果从请求头中提取不到，则重新生成，如下图：

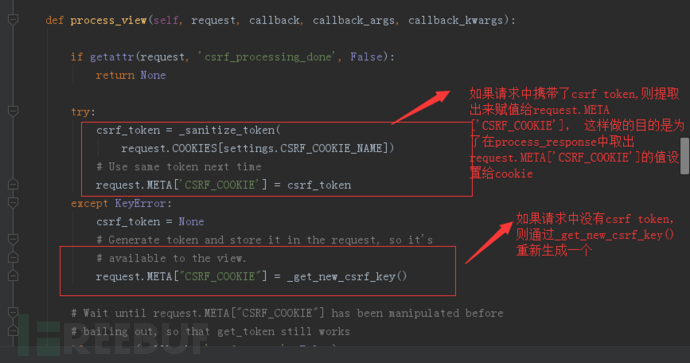
process_response 中会有更新csrf token cookie的功能，如下：

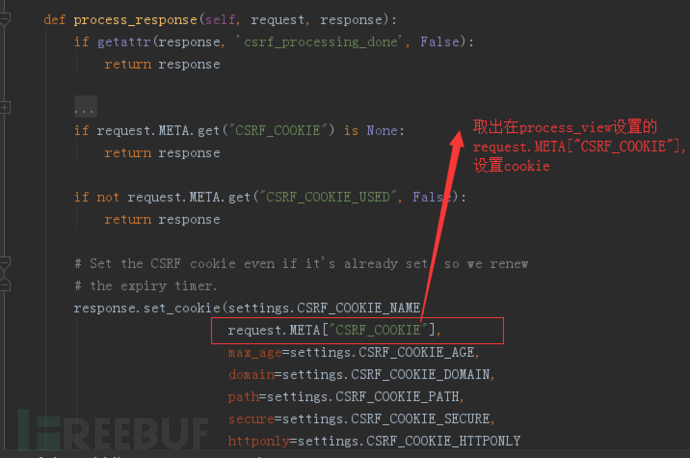
3、通过在视图中修改request.META['CSRF_COOKIE']值实现csrf token 的更新

通过1和2我们就可以知道只要在在response返回之前更新request.META['CSRF_COOKIE']的值，便可以实现每次请求的csrf token 都不一样，当然可以通过修改CsrfViewMiddleware中间件源码的方式实现，不过这种方式的入侵性太大，最好的选择是在视图中修改，因为视图处理流程是在response之前进行，如下：

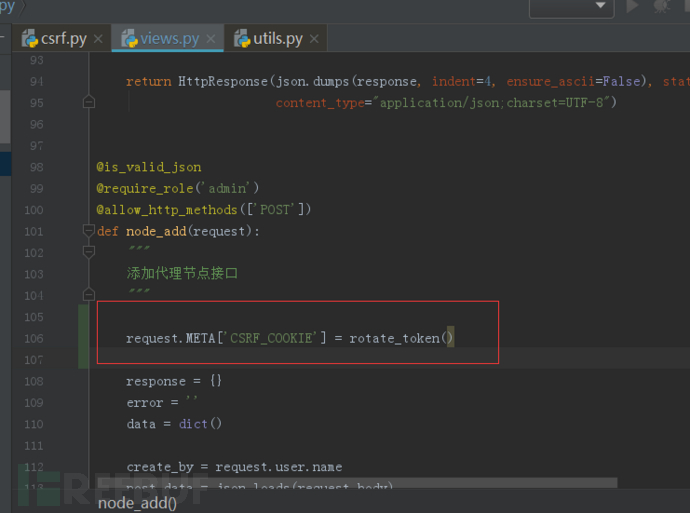
这里的rotate_token则是CsrfViewMiddleware 中间件提供的更新csrf token的接口，如下：

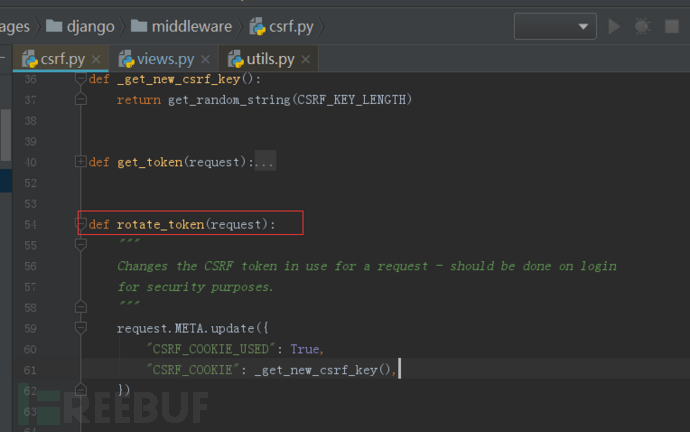
总结

本文提到的这个方法确实可以实现基于请求对csrf_token值进行更新，而不是原先的基于session的，这样更新之后，对于ajax请求倒是没有什么问题，不过对于From表单中csrf_token值的更新是需要进行后端渲染更新的，对于前后端分离的请求，这个不足是可以让后端提供个token 获取接口来实现前端页面中form表单的csrf_token值更新实现，当然也可以对form表单的提交行为进行监听，然后异步提交，这样直接走ajax那条路线，就没啥问题了。