51nod1624 取余最长路 前缀和 + set

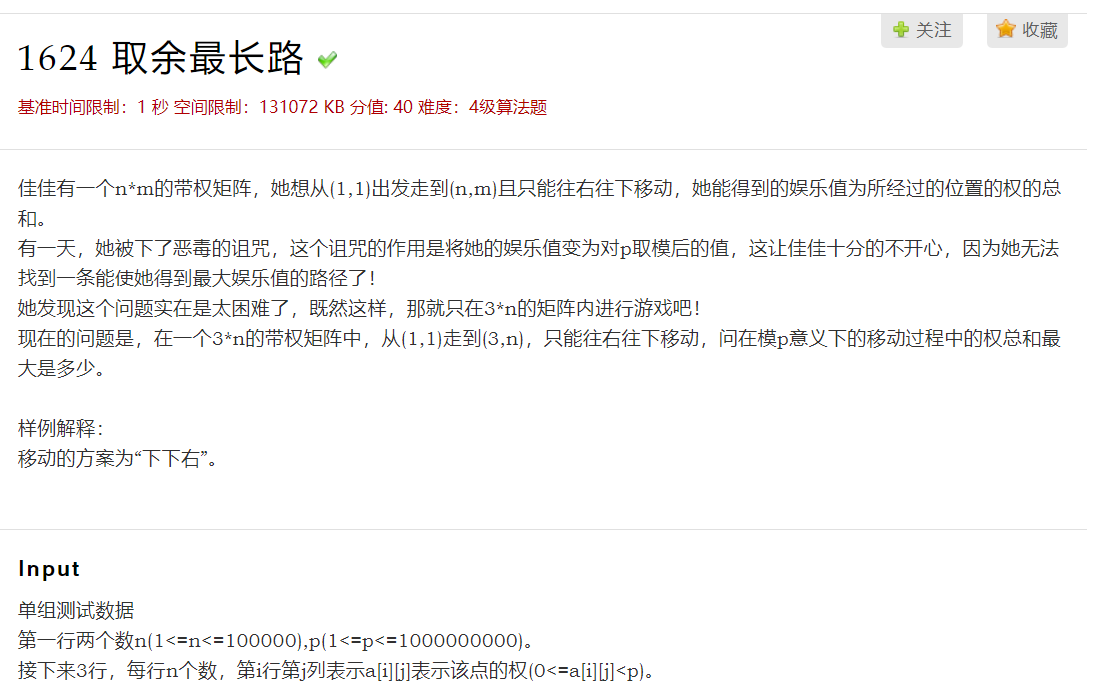
由于只有3行，因此只会会换行2次，假设$x, y$分别为这两次的换行点

那么答案为$S[1][x] +S[2][y] - S[2][x - 1] + S[3][n] - S[3][y - 1]$

其中，$S[i]$表示第$i$行的前缀和

令$a[x] = S[1][x] - S[2][x - 1], b[y] = S[2][y] - S[3][y - 1]$

考虑枚举$x$，那么问题转化为询问在一堆数中求一个数$k$使得$v (= a[x] + S[3][n]) + k \;mod\;p$最大

分两种情况考虑，第一种$v + k \in [v, mod - 1]$，那么$k \in [0, mod - k - 1]$，并且$k$越大越好

第二种不如第一种好，但有可能不得不选，$v + k \in [1, v - 1]$，同样时$k$越大越好

也就是说，需要一种支持插入，查询前驱和最大值的数据结构，$set$就可以

注：倒叙枚举$x$，可以做到不删除

复杂度$O(n \log n)$

#include <set>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
 
extern inline char gc() {
    static char RR[], *S = RR + , *T = RR + ;
    if(S == T) fread(RR, , , stdin), S = RR;
    return *S ++;
}
inline int read() {
    int p = , w = ; char c = gc();
    while(c > '' || c < '') { if(c == '-') w = -; c = gc(); }
    while(c >= '' && c <= '') p = p *  + c - '', c = gc();
    return p * w;
}
 
#define ll long long
#define ri register int
#define sid 200050
 
int n, ans, mod;
int s[][sid], a[sid], b[sid];
 
set <int> ex;
 
int main() {
    n = read(); mod = read();
    for(ri i = ; i <= ; i ++)
    for(ri j = ; j <= n; j ++)
    s[i][j] = (s[i][j - ] + read()) % mod;
 
    for(ri i = ; i <= n; i ++) a[i] = (s[][i] - s[][i - ] + mod) % mod;
    for(ri i = ; i <= n; i ++) b[i] = (s[][i] - s[][i - ] + mod) % mod;
 
    int der = s[][n]; ex.insert();
    for(ri i = n; i >= ; i --) {
        ex.insert(-b[i]);
        int v = (der + a[i]) % mod;
        int p = *ex.lower_bound(-(mod -  - v));;
        if(p == ) ans = max(ans, (v - *(++ ex.begin())) % mod);
        else ans = max(ans, v + -p);
    }
 
    printf("%d\n", ans);
    return ;
}