POJ 3734 Blocks （矩阵快速幂）

题目链接

Description

Panda has received an assignment of painting a line of blocks. Since Panda is such an intelligent boy, he starts to think of a math problem of painting. Suppose there are N blocks in a line and each block can be paint red, blue, green or yellow. For some myterious reasons, Panda want both the number of red blocks and green blocks to be even numbers. Under such conditions, Panda wants to know the number of different ways to paint these blocks.

Input

The first line of the input contains an integer T(1≤T≤100), the number of test cases. Each of the next T lines contains an integer N(1≤N≤10^9) indicating the number of blocks.

Output

For each test cases, output the number of ways to paint the blocks in a single line. Since the answer may be quite large, you have to module it by 10007.

Sample Input

2

1

2

Sample Output

2

6

题意：

给定n个方格排成一列，现在要用红、蓝、黄、绿四种颜色的油漆给这些方格染色。求染成红色的方块数和染成绿色的方块的个数同时位偶数的染色方案的个数，输出对10007取余后的答案。

分析：

我们从最左边开始染色。设染到第i个方块为止，红色和绿色都是偶数的方案数为Ai，红色和绿色恰有一个为偶数的方案数是Bi，红色和绿色都是奇数的方案数是Ci。这样染到第i+1个方格为止，红色和绿色都是偶数的方案数有如下两种可能：

1.到第i个方块为止，红色和绿色都是偶数个，并且第i+1个方块被染成了蓝色或者黄色。

2.到第i个方块为止红色和绿色恰有一个是奇数，并且第i+1个方块染成奇数的那个对应的颜色。

因此，有如下的递推关系：

Ai+1=2 ×Ai +Bi

同理，有

Bi+1=2 × Ai + 2 × Bi + 2 × Ci

Ci+1=bi + 2 × Ci

递推关系可以用矩阵表示如下：

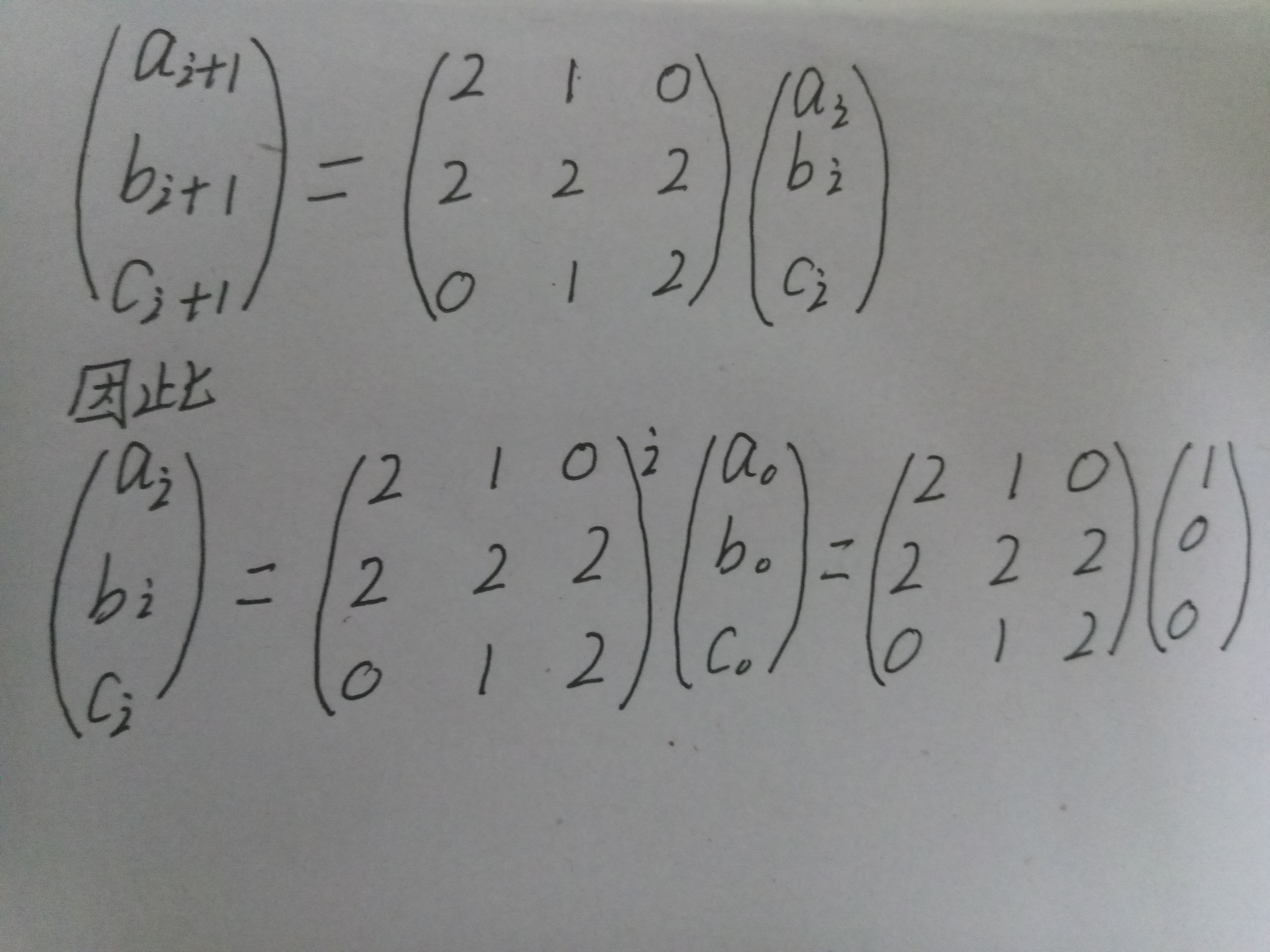
之后就可以用矩阵快速幂求解了。

代码：

#include<iostream>
#include<stdio.h>
#include<string.h>
using  namespace std;
int n;
struct matrix
{
    int tu[10][10];
    matrix()
    {
        memset(tu,0,sizeof(tu));
    }
} A,B;
matrix mul(matrix &A,matrix &B)///定义矩阵的乘法
{
    matrix C;
    for(int i=0; i<3; i++)
        for(int j=0; j<3; j++)
            for(int k=0; k<3; k++)
            {
                C.tu[i][j]=(C.tu[i][j]+(A.tu[i][k]*B.tu[k][j]%10007))%10007;
            }
    return C;
}

matrix quick_mi(matrix A,int b)///求一个矩阵的A的b次方
{
    matrix C;
    for(int i=0; i<3; i++)
        C.tu[i][i]=1;
    while(b)
    {
        if(b&1)
            C=mul(C,A);
        b>>=1;
        A=mul(A,A);
    }
    return C;
}

int main()
{
    int T;
    scanf("%d",&T);
    matrix A;
    while(T--)
    {
        scanf("%d",&n);
        A.tu[0][0]=2;
        A.tu[0][1]=1;
        A.tu[0][2]=0;
        A.tu[1][0]=2;
        A.tu[1][1]=2;
        A.tu[1][2]=2;
        A.tu[2][0]=0;
        A.tu[2][1]=1;
        A.tu[2][2]=2;
        A=quick_mi(A,n);
        printf("%d\n",A.tu[0][0]%10007);
    }
    return 0;
}