【BZOJ4002】[JLOI2015]有意义的字符串 数学

【BZOJ4002】[JLOI2015]有意义的字符串

Description

B 君有两个好朋友，他们叫宁宁和冉冉。有一天，冉冉遇到了一个有趣的题目：输入 b;d;n，求

Input

一行三个整数 b;d;n

Output

一行一个数表示模 7528443412579576937 之后的结果。

Sample Input

1 5 9

Sample Output

76

HINT

其中 0<b^2< = d<(b+1)2< = 10^18,n< = 10^18，并且 b mod 2=1,d mod 4=1

题解：最近数学老师刚讲的特征方程，吓人~

对于数列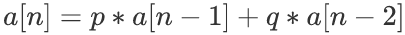

我们设出特征方程x²=px+q，解出特征根x1,x2，则通项公式为

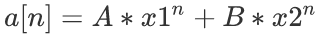
然后根据题意，令x1=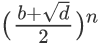，x2=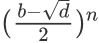，令A=B=1，所以得到a[0]=2,a[1]=b

然后a[n]我们将x1,x2带入特征方程求出p和q，然后用矩阵乘法求出a[n]，剩下一个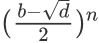，发现它的绝对值是小于1的，那么只有在n为奇数时它才会产生-1的贡献

#include <cstdio>
#include <cstring>
#include <iostream>
#define mod 7528443412579576937ull
using namespace std;
typedef unsigned long long ll;
ll A,C,B,D,n,ans1;
typedef struct matrix
{
	ll v[5][5];
}M;
M ans,x,empty;
ll pmm(ll a,ll b)
{
	ll c=0;
	while(b)
	{
		if(b&1) c=(c+a)%mod;
		a=(a+a)%mod,b>>=1;
	}
	return c;
}
M mmul(M a,M b)
{
	M c=empty;
	int i,j,k;
	for(i=1;i<=2;i++)	for(j=1;j<=2;j++)	for(k=1;k<=2;k++)
		c.v[i][j]=(c.v[i][j]+pmm(a.v[i][k],b.v[k][j]))%mod;
	return c;
}
M pm(ll y)
{
	while(y)
	{
		if(y&1)	ans=mmul(ans,x);
		x=mmul(x,x),y>>=1;
	}
}
int main()
{
	scanf("%llu%llu%llu",&B,&D,&n);
	if(n==0)
	{
		printf("1");
		return 0;
	}
	A=B,C=(D-A*A)/4;
	ans.v[1][1]=A,ans.v[1][2]=2;
	x.v[1][1]=A,x.v[2][1]=C,x.v[1][2]=1;
	pm(n-1);
	printf("%llu",ans.v[1][1]-(C&&(n%2==0)));
	return 0;
}