[agc006E]Rotate 3x3

Description

给你一个3*N的网格，位置为（i，j）的网格上的数为i+3（j-1）。每次选一个3*3的网格旋转180度，问最后能否使得网格（i，j）的值为a_i,j。（5≤N≤10⁵）

如图：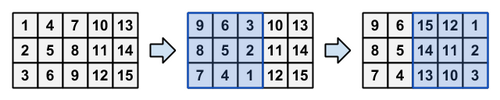

Solution

依图可看出，所谓的旋转就是将选择的3*3网格左右列交换，并且3列都进行翻转。

设正列（如1,2,3）为小写字母，反列（如3,2,1）为大写字母。

假如有相邻5列：

a b c d e

C B A d e

C B E D a

e b c D a

e b A d C

a B E d C

a B c D e

a d C b e

c D A b e

c B a d e

A b C d e

我们可以在有5列可供操纵的情况下将任意相隔1列的两列翻转而不影响其他。

在最终答案中设下标为奇的反列个数为x，下表为偶的个数为y。

先不考虑翻转问题，将奇列和偶列分开考虑（因为在处理奇列的时候只会翻转却不会影响偶列的具体数值）。由于如果初始矩阵操作后变为矩阵a，则矩阵a一定能变为初始矩阵，我们按照列的权值从小到大将矩阵a恢复为初始矩阵。处理奇列时，每翻转一次，就会翻转一个偶列，偶列也是同样道理。我们计算出奇列、偶列被翻转次数的奇偶性，与x、y比较即可。

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
int n,a[][];
int need_swap[],real_swap[];
int num[],id[];
int tree[];
void add(int _id,int x){for(;_id<=n;_id+=_id&-_id) tree[_id]+=x;}
int query(int _id){int re=;for(;_id;_id-=_id&-_id) re+=tree[_id];return re;}
int main()
{
    scanf("%d",&n);
    for (int j=;j<;j++)
    for (int i=;i<=n;i++)
        scanf("%d",&a[j][i]);
    for (int i=;i<=n;i++)
    for (int j=;j<;j++)
    {
        if ((a[][i]^i)&) { printf("No");return ;}
        if (a[][i]==a[][i]+&&a[][i]==a[][i]+&&a[][i]%!=)
        {
            need_swap[i&]++;num[i]=a[][i]/+;id[num[i]]=i;continue;
        }
        if (a[][i]==a[][i]-&&a[][i]==a[][i]-&&a[][i]%!=)
        {
            num[i]=a[][i]/+;id[num[i]]=i;continue;
        }
        printf("No");return ;
    }
    int cnt;
    for (int i=;i<=n;i+=)
    {
        cnt=id[i]+*(i/-query(id[i]));
        real_swap[]+=abs(i-cnt)/;
        add(id[i],);
    }
    memset(tree,,sizeof(tree));
    for (int i=;i<=n;i+=)
    {
        cnt=id[i]+*(i/--query(id[i]));
        real_swap[]+=abs(i-cnt)/;
        add(id[i],);
    }
    real_swap[]%=;real_swap[]%=;need_swap[]%=;need_swap[]%=;
    if (real_swap[]!=need_swap[]||real_swap[]!=need_swap[]) printf("No");
    else printf("Yes");
}