Code Chef IMPO（计算几何+扫描线+积分）

题面

传送门

前置芝士

扫描线，积分求面积

题解

我怎么老是忘了积分可以求面积……

首先，这两个投影的最小的\(x\)坐标和最大的\(x\)坐标必须相等，否则肯定无解

我们考虑一种方法，枚举\(x\)坐标，并令每一个\(x\)处对应的多边形的面积最大。只有每一个\(x\)处面积都取最大，多面体的体积才能取到最大值

怎么样才能让对应的多边形面积最大呢？我们令\(h(c)\)表示\(xy\)平面上\(x=c\)处投影的长度之和，令\(g(c)\)表示\(xz\)平面上\(x=c\)处的投影长度之和。注意，因为投影不一定是个凸多边形，所以\(x=c\)处的投影不一定连续

可以发现\(h(x)\)和\(g(x)\)都是个一次函数（具体怎么发现后面会求的），分别设为\(h(x)=ax+b,g(x)=cx+d\)，那么\(x\)处能取到的最大面积就是\(f(x)=h(x)\times g(x)=acx^2+(ad+bc)x+bd\)，那么\([l,r]\)这一段区间的面积就是

\[\int_{l}^rf(x)=\left|{acx^3\over 3}+{(ad+bc)x^2\over 2}+bdx\right|_l^r=F(r)-F(l)
\]

其中

\[F(x)={acx^3\over 3}+{(ad+bc)x^2\over 2}+bdx
\]

然后我们用扫描线来处理了，引用一下官方题解的图

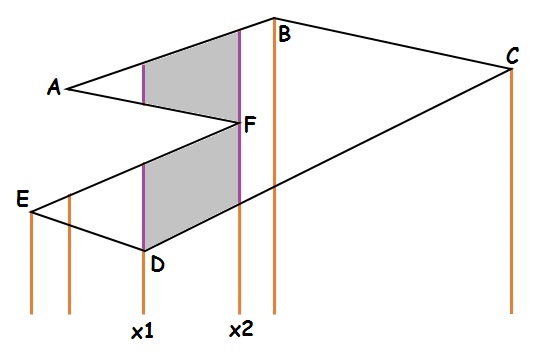
我们要求那块阴影部分的面积，根据上面的讨论，我们只需要知道\([x_1,x_2]\)这段区间内每个\(x\)处阴影的长度是多少。那么就是\(AB\)上该点的\(y\)坐标减去\(AF\)上该点的\(y\)坐标加上\(EF\)减去\(CD\)，这样加入加入或删除直线我们就可以\(O(1)\)维护\(abcd\)了

信心满满交上去发现全\(WA\)，然后发现我们计算面积的时候不能两个定积分相减，因为精度会爆炸，得拆成以下形式

\[F(r)-F(l)=(r-l)\left({ac(l^2+lr+r^2)x^3\over 3}+{(ad+bc)(l+r)x^2\over 2}+bdx\right)
\]

然后精度就没问题了

//minamoto
#include<bits/stdc++.h>
#define R register
#define inf 0x3f3f3f3f
#define inline __inline__ __attribute__((always_inline))
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
int read(){
    R int res,f=1;R char ch;
    while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
    for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
    return res*f;
}
const int N=5e5+5;const double inv3=1.0/3,eps=1e-8;
inline int sgn(R double x){return x<-eps?-x:x;}
struct Point{int x,y;}A[N],B[N];
struct Line{
	double k,b;
	inline Line(){}
	inline Line(R double kk,R double bb):k(kk),b(bb){}
	inline Line(const Point &p,const Point &q){
		k=1.0*(q.y-p.y)/(q.x-p.x),b=p.y-p.x*k;
	}
	inline Line op(){return Line(-k,-b);}
};
struct node{
	Line L;int v;bool k;
	inline bool operator <(const node &b)const{return v<b.v;}
}st[N];int top;
void init(int n,Point *a,bool k){
	a[n+1]=a[1];
	fp(i,1,n)if(a[i].x!=a[i+1].x){
		Point p=a[i],q=a[i+1];Line L(p,q);
		st[++top]={L,p.x,k};
		st[++top]={L.op(),q.x,k};
	}
}
int n,m;
int main(){
//	freopen("testdata.in","r",stdin);
	for(int T=read();T;--T){
		int mxa=-inf,mna=inf,mxb=-inf,mnb=inf;top=0;
		n=read();
		fp(i,1,n)A[i].x=read(),A[i].y=read(),cmax(mxa,A[i].x),cmin(mna,A[i].x);
		m=read();
		fp(i,1,m)B[i].x=read(),B[i].y=read(),cmax(mxb,B[i].x),cmin(mnb,B[i].x);
		if(mxa!=mxb||mna!=mnb){puts("-1");continue;}
		init(n,A,0),init(m,B,1);
		sort(st+1,st+1+top);
		double l,r,res=0,k[2]={0,0},b[2]={0,0};
		for(R int i=1;i<top;){
			l=st[i].v;
			while(i<=top&&!sgn(st[i].v-l)){
				k[st[i].k]+=st[i].L.k,
				b[st[i].k]+=st[i].L.b,
				++i;
			}
			if(i>top)break;
			r=st[i].v;
			res+=(r-l)*(k[0]*k[1]*(l*l+l*r+r*r)*inv3+(l+r)*(b[0]*k[1]+b[1]*k[0])*0.5+b[0]*b[1]);
		}
		printf("%.10lf\n",res);
	}
	return 0;
}