LeetCode214. Shortest Palindrome

Given a string s, you are allowed to convert it to a palindrome by adding characters in front of it. Find and return the shortest palindrome you can find by performing this transformation.

Example 1:

Input: "aacecaaa"
Output: "aaacecaaa"

Example 2:

Input: "abcd"
Output: "dcbabcd"

思路

最简单直接的方法是 brute force，即先求以起始索引为开始位的最长回文字串，然后将剩下的部分逆置直接加到s前即可。这种方法比较耗时，可以使用KMP算法来解这题。

KMP算法

将s和其逆转字符串r连接起来，这肯定是一个回文，在他们中间加一个其它字符构成新的字符串t，然后还需要一个和t长度相同的一位数组next，其中next[i]表示从t[i]到开头的子串的相同前缀后缀的个数，就是KMP算法中的那个next数组。最后把不相同的个数对应的字符串添加到s之前即可。其实和brute force一样都是找以起始索引为开始位的最长回文字串，只不过现在不是遍历各个字符去找，而是利用KMP算法去找。找到后直接将原字符串s除了这个回文字串剩下的部分逆置后加到s前面即可。

下面next数组的计算过程可以参照KMP算法解释连接中最大长度表部分。

对于next[i-1]，加入索引i位置上的字符得到的0~i的字串情况next[i]是如何变化的呢？原来的所有前缀不变，但是多了个前缀，即原来的最长前缀加上i-1位置上的的字符。原来的后缀都要发生变化，因为最后面的字符改掉了，所以原来的所有后缀要加上i位置上的字符，另外还多出了一个后缀，即位置i上的单个字符。

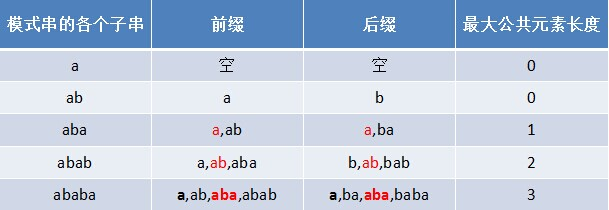
如果next[i-1]是0，即没有匹配的前后缀，那么加上位置i上的字符后前缀后缀也是不匹配的。但是有一种可能会增加前缀后缀的公共最长元素，那就是原来的起始索引处的字符可能等于新加入的i索引位置上的字符，若相等则next[i]=1，否则还是0。

假如next[i-1]不是0，则其值是0到索引i-1位置上的字串中前缀后缀的最大公共元素长度（能够匹配的最长前缀后缀，且注意前缀一直是从0开始的，这样的话最长前缀加上其长度就是其在前后缀比较过程中不匹配的字符索引位置）。

next[i] -- 0~i处匹配的最长前缀后缀的长度。

代码

解释

public String shortestPalindrome(String s) {
    String temp = s + "#" + new StringBuilder(s).reverse().toString();
    int[] table = getTable(temp);

    //get the maximum palin part in s starts from 0
    return new StringBuilder(s.substring(table[table.length - 1])).reverse().toString() + s;
}

public int[] getTable(String s){
    //get lookup table
    int[] table = new int[s.length()];

    //pointer that points to matched char in prefix part
    int index = 0;
    //skip index 0, we will not match a string with itself
    for(int i = 1; i < s.length(); i++){
        if(s.charAt(index) == s.charAt(i)){ //一开始i=1,index=0,比较s[0]和s[1],如果相等那么table[1]=1,index=1
            //we can extend match in prefix and postfix
            table[i] = table[i-1] + 1; //
            index ++;
        }else{
　　　　　　　//因为index指向table[i-1]的最长匹配前缀的末位置字符，如果这个字符不等于位置i上的字符则断定原来的最长前缀肯定不匹配任何后缀(因为后缀以末字符为尾)
　　　　　　　//假设原来的最长匹配前缀是s[0~2],那么可以得出s[0~3]，s[0~4]这些比最长匹配前缀要长的前缀肯定是不匹配后缀的，而新的后缀无非就是后面加了个字符，
　　　　　　　//那么这些前缀肯定也不能匹配新的后缀，但是如果原来i-1位置上的字符等于i位置上的字符而index这时指向的是i-1位，则便是上面if的情形
　　　　　　　//table[i]表示在s[0~i]中匹配的最长前缀的末字符位置，如果table[5]=2则表示s[0~5]中匹配的最长前缀是s[0~2],让index来指向这个末位置字符。
            index = table[i-1];
            while(index > 0 && s.charAt(index) != s.charAt(i)){
　　　　　　　　　 //we will try to shorten the match string length until we revert to the beginning of match (index 1)
                index = table[index-1];
            }

            //when we are here may either found a match char or we reach the boundary and still no luck
            //so we need check char match
            if(s.charAt(index) == s.charAt(i)){
                //if match, then extend one char
                index ++ ;
            }
            table[i] = index;
        }
    }

    return table;
}