leetcode每日一题：对角线上的质数

题目

2614. 对角线上的质数

给你一个下标从 0 开始的二维整数数组 nums 。

返回位于 nums 至少一条 对角线 上的最大 质数 。如果任一对角线上均不存在质数，返回 0 。

注意：

• 如果某个整数大于 1 ，且不存在除 1 和自身之外的正整数因子，则认为该整数是一个质数。
• 如果存在整数 i ，使得 nums[i][i] = val 或者 nums[i][nums.length - i - 1]= val ，则认为整数 val 位于 nums 的一条对角线上。

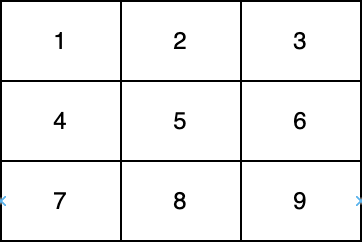
在上图中，一条对角线是 [1,5,9] ，而另一条对角线是 [3,5,7] 。

示例 1：

输入：nums = [[1,2,3],[5,6,7],[9,10,11]]
输出：11
解释：数字 1、3、6、9 和 11 是所有 "位于至少一条对角线上" 的数字。由于 11 是最大的质数，故返回 11 。

示例 2：

输入：nums = [[1,2,3],[5,17,7],[9,11,10]]
输出：17
解释：数字 1、3、9、10 和 17 是所有满足"位于至少一条对角线上"的数字。由于 17 是最大的质数，故返回 17 。

提示：

• 1 <= nums.length <= 300
• nums.length == numsi.length
• 1 <= nums[i][j] <= 4*106

思路

​ 本题没什么弯弯绕绕，直接模拟即可。由于在提示中限制了nums.length == numsi.length，2条对角线都是完整的，不需要额外考虑边界：

• 第1条对角线nums[i][i]
• 第2条对角线nums[i][n-1-i]

判断质数

​ 对于1个正整数n，如何判断它是不是质数呢？

​ 可以先假设n是合数，那么n必然可以分解成n = x * y，x <= y（仅为说明问题，如果 x > y，那么可以交换 x 和 y 来满足 x <= y），显然 x <= sqrt(n)。所以，可以遍历[2, sqrt(n)]，如果n能整除其中某个数，就一定是合数。

​ 还有一个额外的注意点是：1既不是质数，也不是合数，需要单独额外判断。

代码

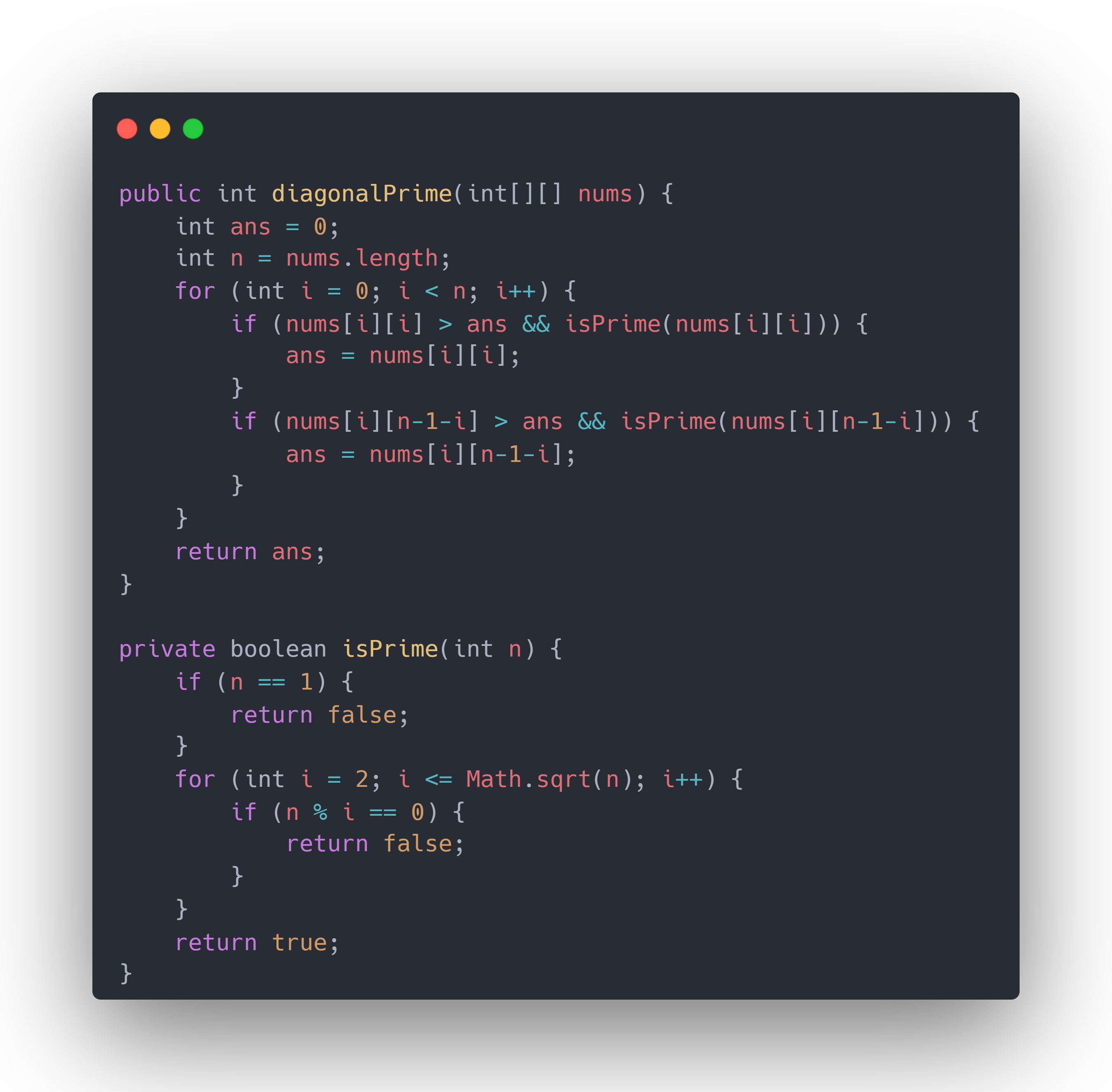
public int diagonalPrime(int[][] nums) {
    int ans = 0;
    int n = nums.length;
    for (int i = 0; i < n; i++) {
        if (nums[i][i] > ans && isPrime(nums[i][i])) {
            ans = nums[i][i];
        }
        if (nums[i][n-1-i] > ans && isPrime(nums[i][n-1-i])) {
            ans = nums[i][n-1-i];
        }
    }
    return ans;
}
private boolean isPrime(int n) {
    if (n == 1) {
        return false;
    }
    for (int i = 2; i <= Math.sqrt(n); i++) {
        if (n % i == 0) {
            return false;
        }
    }
    return true;
}

​ 这里还有1个小优化：由于isPrime方法需要遍历[2, sqrt(n)]这个范围，相对于nums[i][i] > ans这个判断是比较耗时的，所以我们在写if条件的时候，可以把isPrime方法写在后面，这样如果前面不满足就会短路掉，加快处理的速度。

耗时

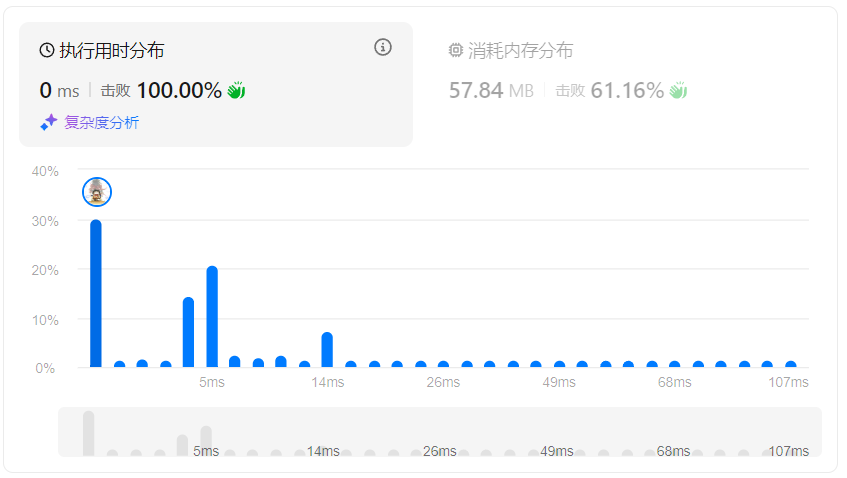
预处理

​ 考虑到提示中给出的数的范围[1, 4 * 10^6]，这个范围不是很大，在判断质数这一步，我们可以先预处理，求出范围内所有的质数，这样就不用每次调用isPrime方法判断了。这里用到的方法是打表求质数，打表的方式可以简单理解为isPrime方法的逆向：我们不直接从n出发，而是从因子出发，如果n = x * y，n 可以看作是 x 的 y 被，我们把范围内所有的满足 x 的 y 倍的数，都标记成合数，那么剩余的，就都是质数了。同样的，这里也需要对1这个既不是质数，也不是合数的特殊值，进行额外判断。

​ 预处理的优点是，我们保存预处理的结果后，后续的质数判断这一步会变快，当然也付出了存储空间和预处理时间的代价。如果我们的二维数组很大，需要判断是否是质数的次数很大，这个预处理的消耗就会比较值得；如果二维数组很小，且数值的理论范围很大，实际范围比较小，就得不偿失了。

代码

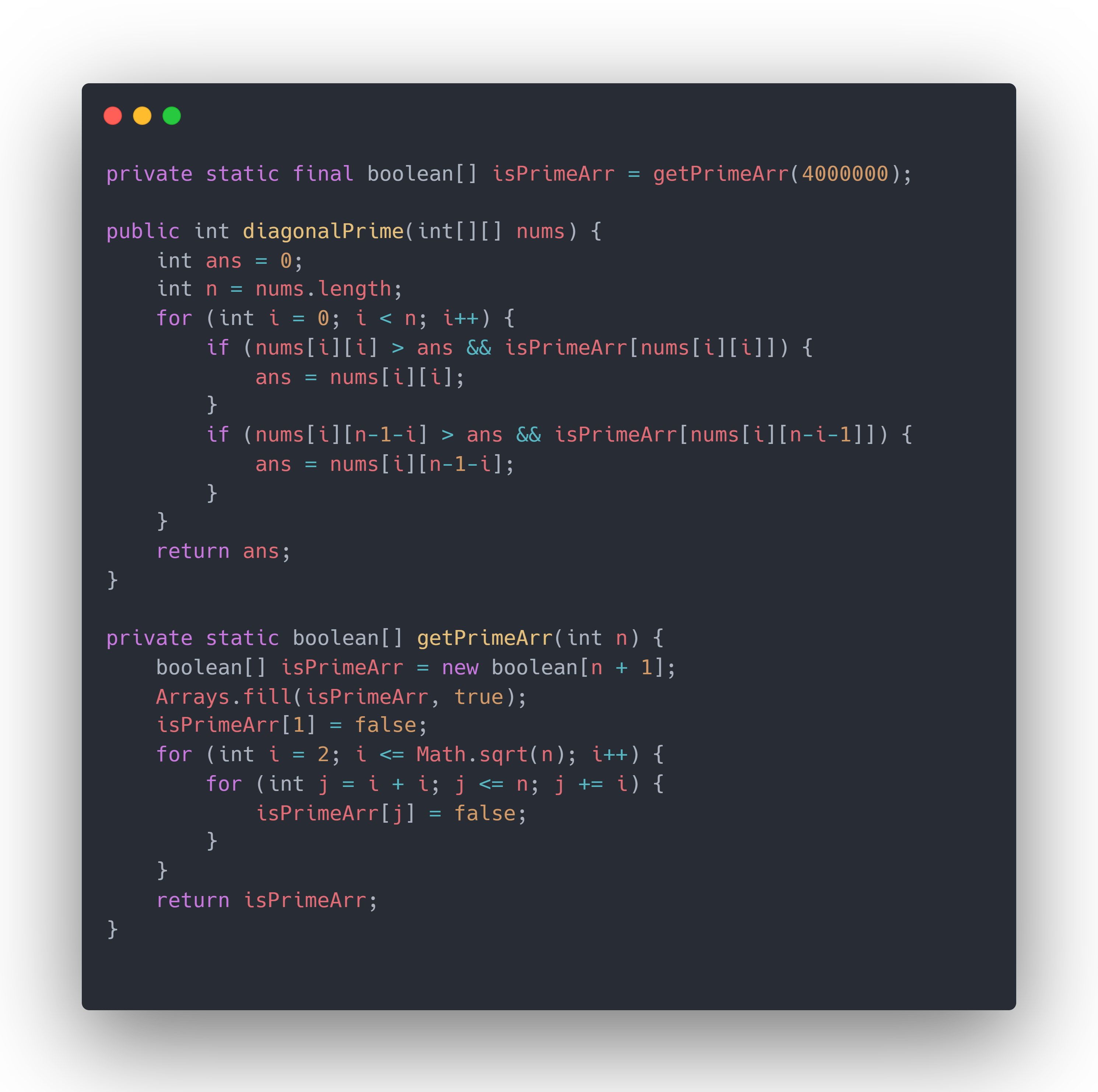
private static final boolean[] isPrimeArr = getPrimeArr(4000000);
public int diagonalPrime(int[][] nums) {
    int ans = 0;
    int n = nums.length;
    for (int i = 0; i < n; i++) {
        if (nums[i][i] > ans && isPrimeArr[nums[i][i]]) {
            ans = nums[i][i];
        }
        if (nums[i][n-1-i] > ans && isPrimeArr[nums[i][n-i-1]]) {
            ans = nums[i][n-1-i];
        }
    }
    return ans;
}
private static boolean[] getPrimeArr(int n) {
    boolean[] isPrimeArr = new boolean[n + 1];
    Arrays.fill(isPrimeArr, true);
    isPrimeArr[1] = false;
    for (int i = 2; i <= Math.sqrt(n); i++) {
        for (int j = i + i; j <= n; j += i) {
            isPrimeArr[j] = false;
        }
    }
    return isPrimeArr;
}

耗时