把KMP算法嚼碎了喂给你吃！（C++）

相信不少人在学数据结构的时候都被KMP算法搞的迷迷糊糊的，原理看的似懂非懂，代码写不出来，或者写出来了也不知道为什么就可以这么写。本文力求尽可能通俗详细的讲解KMP算法，让你不再受到KMP算法的困扰。

暴力匹配的痛点

所谓暴力匹配，就是从文本串的首端开始依次检查子串是否与模式串匹配，如果不匹配就将模式串往后移一个位置，从头开始匹配，直到在某处成功匹配或匹配到末尾也没能成功匹配。如下图：

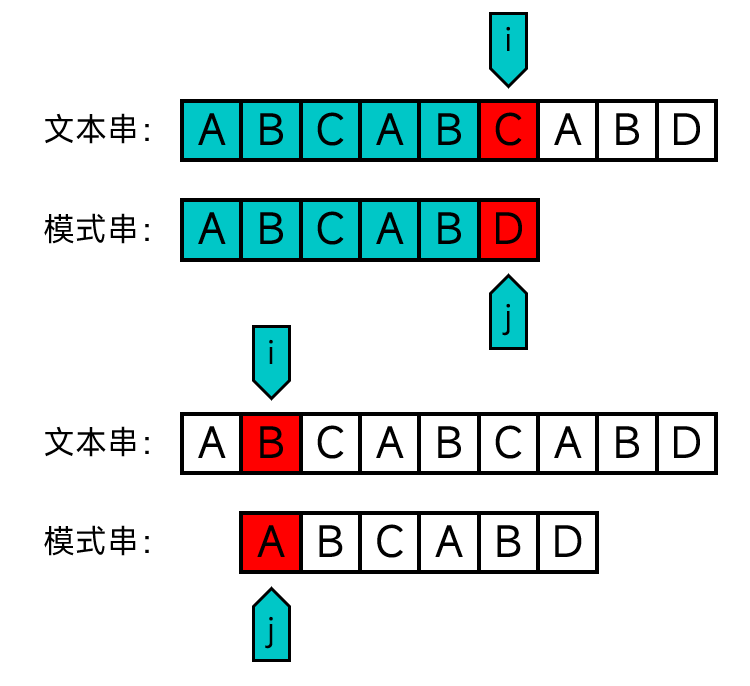
设文本串为T，模式串为P，i为文本串中的下标，j为模式串中的下标，文本串的长度为m，模式串的长度为n，则代码如下：

int bruteForce(std::string t, std::string p) {
    int i = 0, j = 0;
    int m = t.length(), n = p.length();
    while (i < m && j < n) {
        if (t[i] == p[j]) {
            i++; j++;
        } else {
            i = i - j + 1;
            j = 0;
        }
    }
    return j == n ? i - j : -1;
}

那么暴力匹配的时间效率如何呢？不难发现，每一次匹配中，我们都需要花费\(O(n)\)的时间成本来判断子串是否与模式串匹配，而总共的判断次数最多为\(m-n+1\)，由于实际情况下有\(m>>n\)，因此\(m-n+1\)近似等于\(m\)，整个暴力匹配的时间复杂度为\(O(mn)\)，显然不理想。

经过观察，我们不难发现，暴力匹配方法做了很多次不必要的匹配。在第一轮发现不匹配的时候，我们无需只将模式串后移一个位置，而是后移到文本串中下标为3的位置（第二个A），并直接从文本串中下标为5的位置（第2个C）开始匹配。从相对运动的角度来讲，也就是将j前移为2，而i不用回退。

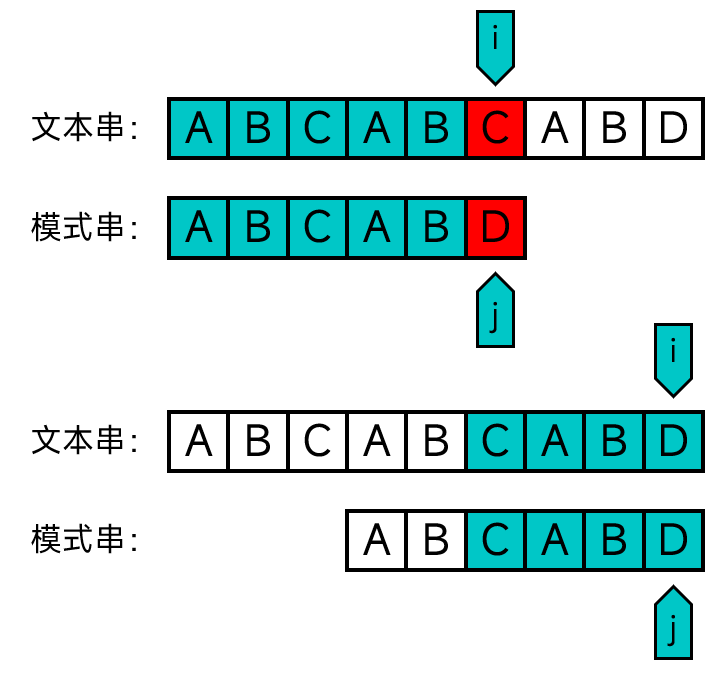
KMP算法

事实上，之所以这么做，是因为模式串中j前面的某些字符恰好与模式串的某个前缀相等。如果你想到了这点，那你的想法刚好就跟发明KMP算法的那三个人的想法一样了（认真）。KMP算法就利用了这一点，每次匹配失败的时候不直接从头开始继续匹配，而是将j回溯到这个前缀后面的字符，而i不用回退，以解决暴力匹配算法的这一痛点。如图：

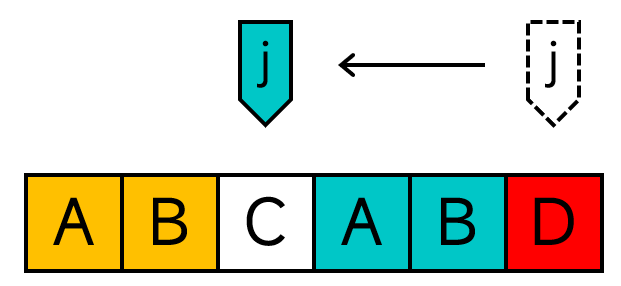
构建next数组

为了应对各种匹配失败的情况，我们需要另开一个与模式串等长的数组next，其中next[j]表示P[j]与T[i]匹配失败的情况下，j要移动到的下标。（显然，对于任意的j，一定有next[j] < j）按照上面那个性质，P[next[j]]之前的p个字符也与P[j]左边的p个字符相等。（其中p为P[next[j]]之前的字符数量）（这一点非常重要，可以说是next数组构建算法的灵魂！）

接下来的一个问题就是，如何判定某次匹配过程失败后，j该移到哪个位置呢？

我们可以用递推的思路来求解。

考虑模式串的第一个字符就不与文本串中的相应字符匹配的情况。如图：

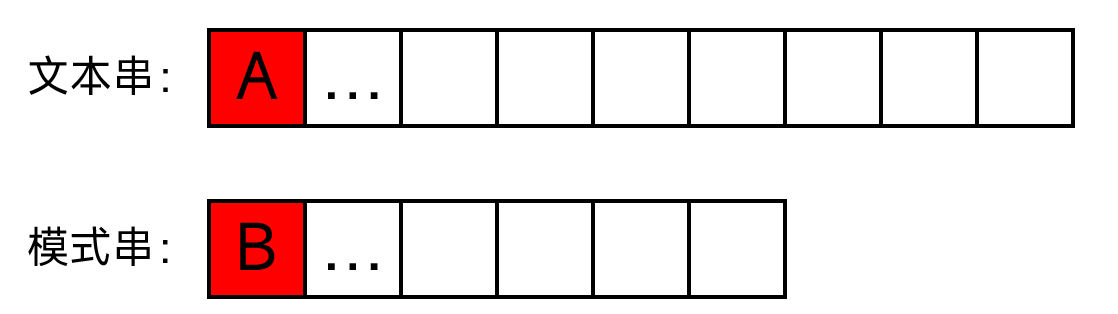
这个时候我们需要将i往后移，不妨将next[0]设为-1。（后面你就会看到这样做自有其精妙之处）

再来考虑next[k]已知的情况，如何求得next[k+1]呢？分两种情况讨论：

第一种情况，P[k]==P[next[k]]，如下图。由上面那条性质，P[k]之前的p个字符与P[next[k]]之前的p个字符相等。而P[k]又是等于P[next[k]]的，因此，P[k+1]之前的p+1个字符与P[next[k]+1]之前的p+1个字符相等。所以，next[k+1]应该设为next[k]+1，以符合上面那条性质。

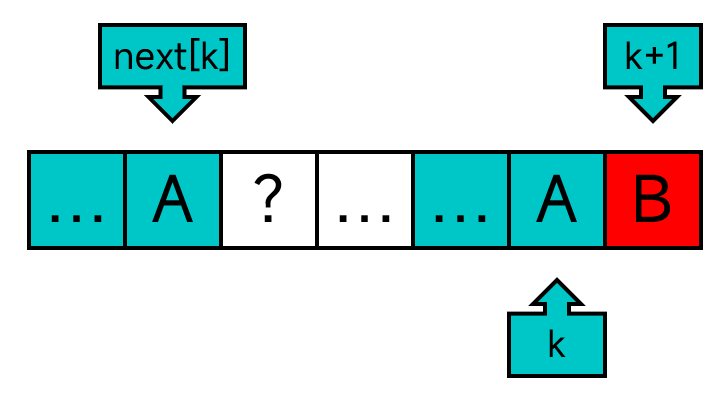
第二种情况，P[k]!=P[next[k]]，如下图。（这里我用不同的颜色标出来了）

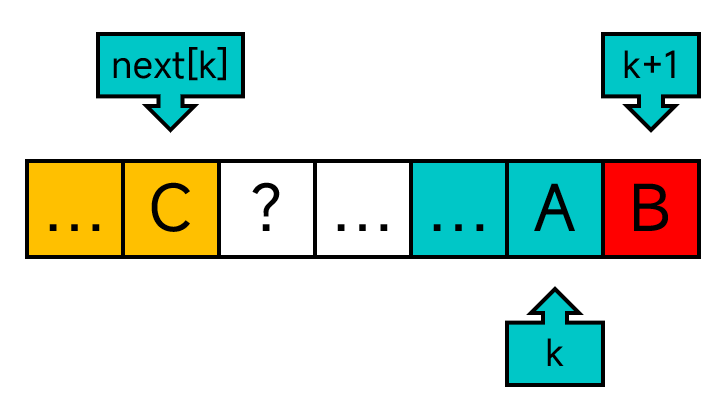
怎么办呢？再考虑P[next[next[k]]]与P[k]之间的关系。

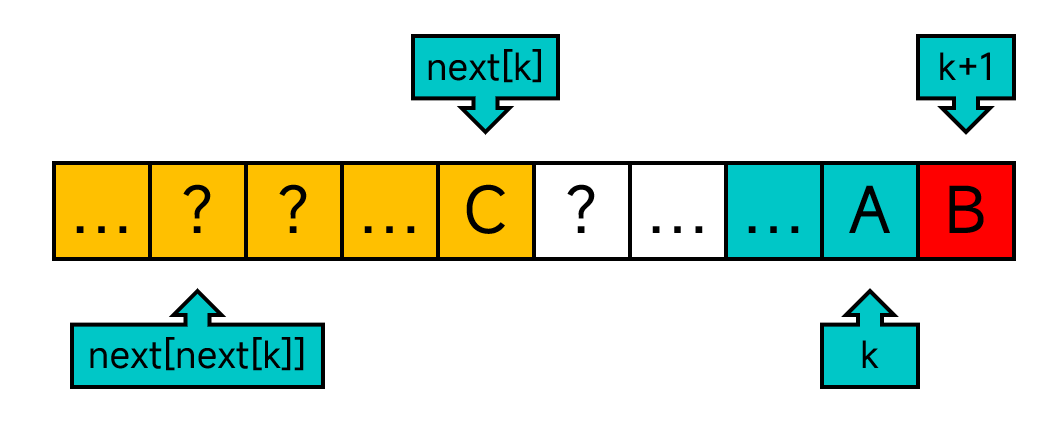
此时的思路与上面相似，如果P[k]==P[next[next[k]]]，就将next[k+1]设为next[next[k]]+1，否则就依次检查next[next[next[k]]]、next[next[next[next[k]]]]、...

不难看出，接受检查的下标是依次递减的，但是递减也得有个限度；另外next[0]永远为-1，因此递减到-1的时候，就说明一直检查到P的第一个字符也没检查到与P[k]相等的字符。此时next[k+1]前面有0个字符与P中长度为0的前缀相等。因此j需要回溯到0，将next[k+1]设为0。

将以上思路稍作整理，可得在next[k]已知的情况下，求得next[k+1]的步骤：

令t为next[k]。
如果t等于-1，就将next[k+1]设为0。
否则，检查P[k]是否等于P[t]。如果等于，就将next[k+1]设为t+1；否则，将t设为next[t]，跳转到第2步。

细心的你可能已经发现了，既然next[0]为-1，-1再加上1刚好也等于0，因此两个条件可以合并起来，上述步骤可以优化一下：

令t为next[k]。
如果t等于-1，或者P[k]等于P[t]，就将next[k+1]设为t+1。
否则，将t设为next[t]，跳转到第2步。

现在你应该看到将next[0]设为-1这种做法的巧妙之处了吧！

这样，由于next[0]事先约定为-1，而由next[0]可以求得next[1]，由next[1]可以求得next[2]...，因此我们就可以得出构建next数组的步骤：

初始化next数组，令其长度为n。
将next[0]设为-1。
初始化k为0，循环执行以下步骤，每次循环完k就加一，如果k加到了n-1就退出循环。
令t为next[k]。
如果t等于-1，或者P[k]等于P[t]，就将next[k+1]设为t+1。
否则，将t设为next[t]，跳转到第5步。

代码实现：

std::vector<int> buildNext(std::string p) {
    int n = p.length();
    std::vector<int> next(n);
    next[0] = -1;
    for (int k = 0; k < n - 1; k++) {
        int t = next[k];
        while (t != -1 && p[k] != p[t]) {
            t = next[t];
        }
        next[k + 1] = t + 1;
    }
    return next;
}

KMP主算法

有了next数组，一切都好办了。

每次匹配的时候，如果匹配成功了就i与j同时往后移一个位置，匹配失败的话j设为next[j]。如果j为-1的话，i就往后移，同时j设为0。

int kmp(std::string t, std::string p) {
    int m = t.length(), n = p.length();
    int i = 0, j = 0;
    auto next = buildNext(p);
    while (i < m && j < n) {
        if (j < 0 || t[i] == p[j]) {
            i++; j++;
        } else {
            j = next[j];
        }
    }
    return j == n ? i - j : -1;
}

复杂度分析

不难看出，KMP算法的空间复杂度（不计T和P本身所占的内存空间）为\(O(n)\)，这是来自next数组所占用的空间开销。

那么时间复杂度为多少呢？网上大多数博文直接在这里放个结论，缺少必要的分析，读者只是知道了结论，至于为什么是这样则是一头雾水。

整个KMP算法的时间复杂度分为以下两部分：

构建next数组的时间复杂度；
匹配的时间复杂度。

其中，构建next数组的时间复杂度为多少呢？

这主要取决于给next数组各项赋值的时间复杂度和对t赋值的次数。

显而易见，前者的时间复杂度为\(O(n)\)。那后者的时间复杂度怎么计算呢？

注意到，每次for循环的结尾，有一个next[k + 1] = t + 1;的语句，而下一次for循环开始时，由于k自增了1，因此int t = next[k];里的next[k]其实就是上一次循环里的next[k + 1]，这条语句执行后的新t其实就是旧t加上1，可以等效的认为对t进行了一次++运算。显而易见，t++的次数为n-1。而while循环里面t = next[t];的最坏次数怎么计算呢？我们知道，next[t]是必然小于t的，所以这条语句执行后t是要往回跳的。但是跳一次跨越的步数是大于等于1的，而往回跳的极限是-1，所以同样的长度，往前跳的次数是n-1，往后跳的次数必然不超过n-1，所以对t赋值的次数（不如说是t跳跃的次数）不会超过2n-2，当然就是\(O(n)\)量级的。所以，构建next数组的时间复杂度为\(O(n)\)。

而匹配的时间复杂度又是多少呢？

这主要取决于while循环执行的次数，而while循环是否执行取决于i和j的取值，因此这也取决于对i和j赋值的次数。

对i赋值的操作只有i++这一条语句，显然这条语句最多会执行m次。

对j的赋值（或者说是跳跃）呢，分析思路与上述类似，包括往前跳跃（j++）和往后跳跃（j = next[j]）。其中前者是与i“携手并进”的，因此执行次数也不会超过m。往后跳跃的次数同样不会超过往前跳跃的次数（原因与上述分析一致）。因此，j的跳跃次数也是\(O(m)\)量级的。

因此，匹配的时间复杂度是\(O(m)\)。

综上所述，整个KMP算法的时间复杂度为\(O(m+n)\)，比暴力算法的\(O(mn)\)要好得多。

这就完美了吗？

考虑下面的情况：

文本串：AAAABAAAAA

模式串：AAAAA

如果我们用KMP算法进行匹配的话，会由于T[4] != P[4]发生一次匹配失败：

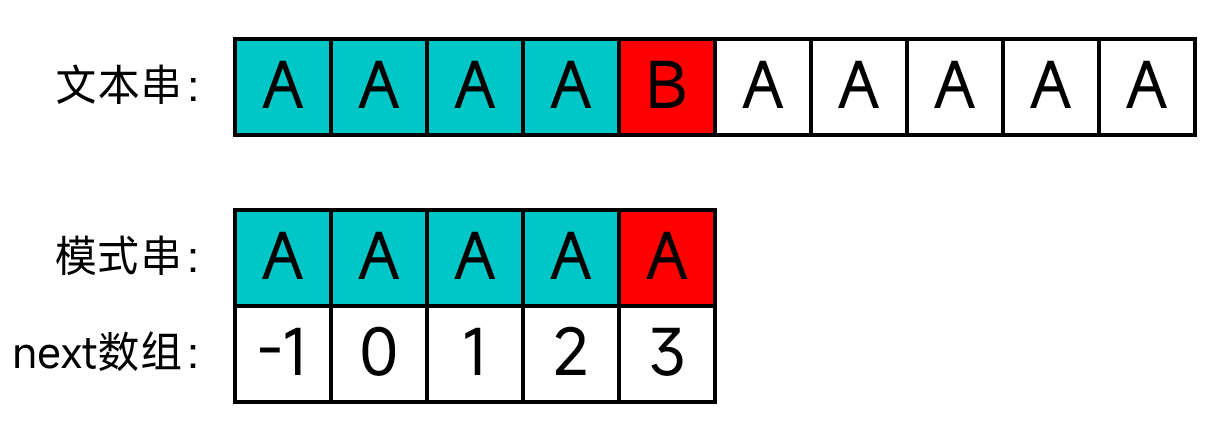
根据next数组的指示，将会由P[3]继续匹配T[4]：

然后是P[2]、P[1]、P[0]，最后因为P[0]与T[4]匹配失败而开始T[5]与P[0]的比对。

但是，明眼人一眼就能看出，T[4]与P[4]比对失败后可以直接进行T[5]与P[0]之间的比对，不需要进行T[4]与P[3]、P[2]...P[0]之间的比对了，因为P[4]和P[3]、P[2]...P[0]是一样的，既然T[4]与P[4]比对失败了，那么T[4]与P[3]、P[2]...P[0]之间的比对就一定会失败，就像推销员给你推销某样产品，你不感兴趣，对方一直喋喋不休，只会让你感到厌烦。

改进

那怎样才能在一次比对失败后不再比对P中相同的字符，而是从不相同的字符开始比对呢？换句话说，如何在比对失败后，能够让j一次性跳转到不一样的字符呢？我们只需要对构建next数组的代码稍作修改。在给next[j+1]赋值的时候，我们还需要检查next[k+1]是否等于next[t+1]。如果等于的话，就赋值为next[t+1]。否则才赋值为t+1。如图：

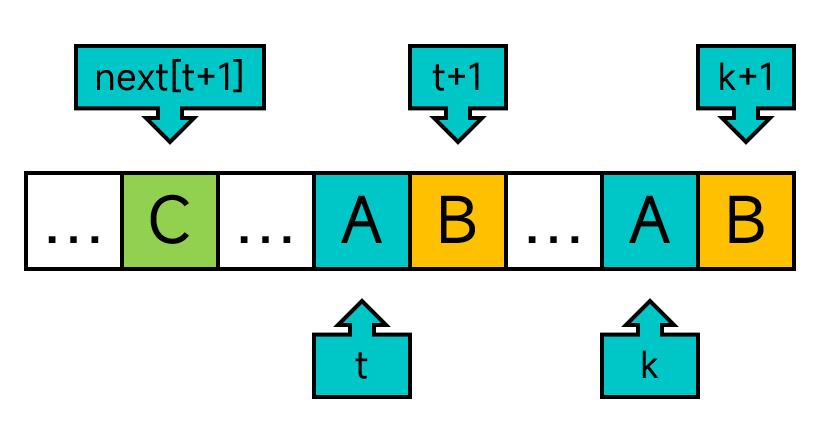
但是直接这样改的话，每次for循环后的t就不一定等于上一次循环的t加1了，所以我们要显式的维护变量t。

std::vector<int> buildNext() {
    int n = p.length();
    std::vector<int> next(n);
    next[0] = -1;
    int t = -1;
    for (int k = 0; k < n - 1; k++) {
        while (t != -1 && p[k] != p[t]) {
            t = next[t];
        }
        next[k + 1] = p[k + 1] == p[t + 1] ? next[t + 1] : t + 1;
        t++;
    }
    return next;
}

显然，时间复杂度是不变的，但是因为跳跃次数减少了，整个算法的效率也会提升。