论文解读（VGAE）《Variational Graph Auto-Encoders》

Paper Information

Title：Variational Graph Auto-Encoders
Authors：Thomas Kipf, M. Welling
Soures：2016, ArXiv
Others：1214 Citations, 14 References

1 A latent variable model for graph-structured data

　　VGAE 使用了一个 GCN encoder 和 一个简单的内积 decoder ，架构如下图所示：

　　

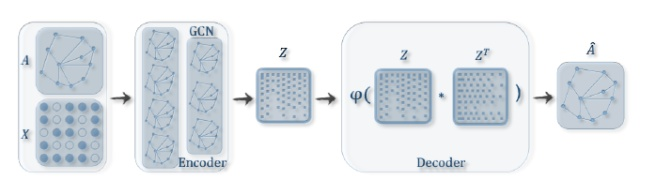
　　Definitions：We are given an undirected, unweighted graph  $\mathcal{G}=(\mathcal{V}, \mathcal{E})$  with  $N=|\mathcal{V}|$  nodes. We introduce an adjacency matrix  $\mathbf{A}$  of  $\mathcal{G}$  (we assume diagonal elements set to $1$ , i.e. every node is connected to itself) and its degree matrix  $\mathbf{D}$ . We further introduce stochastic latent variables  $\mathbf{z}_{i}$ , summarized in an  $N \times F$  matrix  $\mathbf{Z}$ . Node features are summarized in an  $N \times D$  matrix  $\mathbf{X}$ .

　　Inference model：使用一个两层的 GCN 推理模型

　　　　$q(\mathbf{Z} \mid \mathbf{X}, \mathbf{A})=\prod_{i=1}^{N} q\left(\mathbf{z}_{i} \mid \mathbf{X}, \mathbf{A}\right) \text { with } \quad q\left(\mathbf{z}_{i} \mid \mathbf{X}, \mathbf{A}\right)=\mathcal{N}\left(\mathbf{z}_{i} \mid \boldsymbol{\mu}_{i}, \operatorname{diag}\left(\boldsymbol{\sigma}_{i}^{2}\right)\right)$

　　其中：

• • $\boldsymbol{\mu}=\operatorname{GCN}_{\boldsymbol{\mu}}(\mathbf{X}, \mathbf{A})$  is the matrix of mean vectors  $\boldsymbol{\mu}_{i} $；　
  • $\log \boldsymbol{\sigma}=\mathrm{GCN}_{\boldsymbol{\sigma}}(\mathbf{X}, \mathbf{A})$；　

def encode(self, x, adj):
    hidden1 = self.gc1(x, adj)
    return self.gc2(hidden1, adj), self.gc3(hidden1, adj)    

mu, logvar = self.encode(x, adj)

　　GCN 的第二层分别输出 mu，log $\sigma$ 矩阵，共用第一层的参数。

　　这里 GCN 定义为：
　　　　$\operatorname{GCN}(\mathbf{X}, \mathbf{A})=\tilde{\mathbf{A}} \operatorname{ReLU}\left(\tilde{\mathbf{A}} \mathbf{X} \mathbf{W}_{0}\right) \mathbf{W}_{1}$

　　其中：

• • $\mathbf{W}_{i}$ 代表着权重矩阵
  • $\operatorname{GCN}_{\boldsymbol{\mu}}(\mathbf{X}, \mathbf{A})$ 和 $\mathrm{GCN}_{\boldsymbol{\sigma}}(\mathbf{X}, \mathbf{A})$ 共享第一层的权重矩阵 $\mathbf{W}_{0} $
  • $\operatorname{ReLU}(\cdot)=\max (0, \cdot)$
  • $\tilde{\mathbf{A}}=\mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}}$ 代表着  symmetrically normalized adjacency matrix

　　至于 $z$ 的生成：

def reparameterize(self, mu, logvar):
    if self.training:
        std = torch.exp(logvar)
        eps = torch.randn_like(std)
        return eps.mul(std).add_(mu)
    else:
        return mu

z = self.reparameterize(mu, logvar)

　　Generative model：我们的生成模型是由潜在变量之间的内积给出的：

　　　　$p(\mathbf{A} \mid \mathbf{Z})=\prod_{i=1}^{N} \prod_{j=1}^{N} p\left(A_{i j} \mid \mathbf{z}_{i}, \mathbf{z}_{j}\right) \text { with } p\left(A_{i j}=1 \mid \mathbf{z}_{i}, \mathbf{z}_{j}\right)=\sigma\left(\mathbf{z}_{i}^{\top} \mathbf{z}_{j}\right)$

　　其中：

• • $\mathbf{A}$ 是邻接矩阵 　　
  • $\sigma(\cdot)$ 是 logistic sigmoid function.　　

class InnerProductDecoder(nn.Module):
    """Decoder for using inner product for prediction."""

    def __init__(self, dropout, act=torch.sigmoid):
        super(InnerProductDecoder, self).__init__()
        self.dropout = dropout
        self.act = act

    def forward(self, z):
        z = F.dropout(z, self.dropout, training=self.training)
        adj = self.act(torch.mm(z, z.t()))
        return adj

self.dc = InnerProductDecoder(dropout, act=lambda x: x)

adj = self.dc(z)

　　Learning：优化变分下界 $\mathcal{L}$ 的参数 $W_i$ ：

　　　　$\mathcal{L}=\mathbb{E}_{q(\mathbf{Z} \mid \mathbf{X}, \mathbf{A})}[\log p(\mathbf{A} \mid \mathbf{Z})]-\mathrm{KL}[q(\mathbf{Z} \mid \mathbf{X}, \mathbf{A}) \| p(\mathbf{Z})]$

　　其中：

• • $\operatorname{KL}[q(\cdot) \| p(\cdot)]$ 代表着 $q(\cdot)$  和  $p(\cdot)$ 之间的 KL散度。　　
  • 高斯先验 $p(\mathbf{Z})=\prod_{i} p\left(\mathbf{z}_{\mathbf{i}}\right)=\prod_{i} \mathcal{N}\left(\mathbf{z}_{i} \mid 0, \mathbf{I}\right)$　　

　　 Non-probabilistic graph auto-encoder (GAE) model

　　计算表示向量 $Z$ 和重建的邻接矩阵 $\hat{\mathbf{A}}$

　　　　$\hat{\mathbf{A}}=\sigma\left(\mathbf{Z Z}^{\top}\right), \text { with } \quad \mathbf{Z}=\operatorname{GCN}(\mathbf{X}, \mathbf{A})$

2 Experiments on link prediction

　　引文网络中链接预测任务的结果如 Table 1 所示。

　　

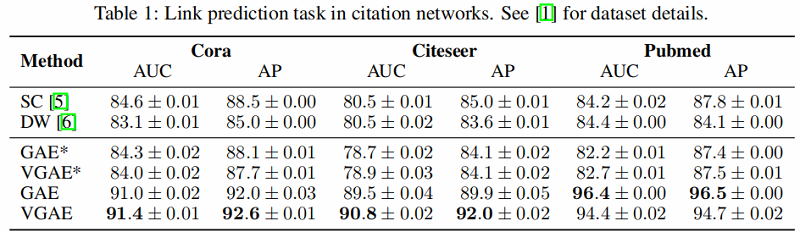
　　GAE* and VGAE* denote experiments without using input features, GAE and VGAE use input features.