JZOJ 4270.【NOIP2015模拟10.27】魔道研究

魔道研究

题面

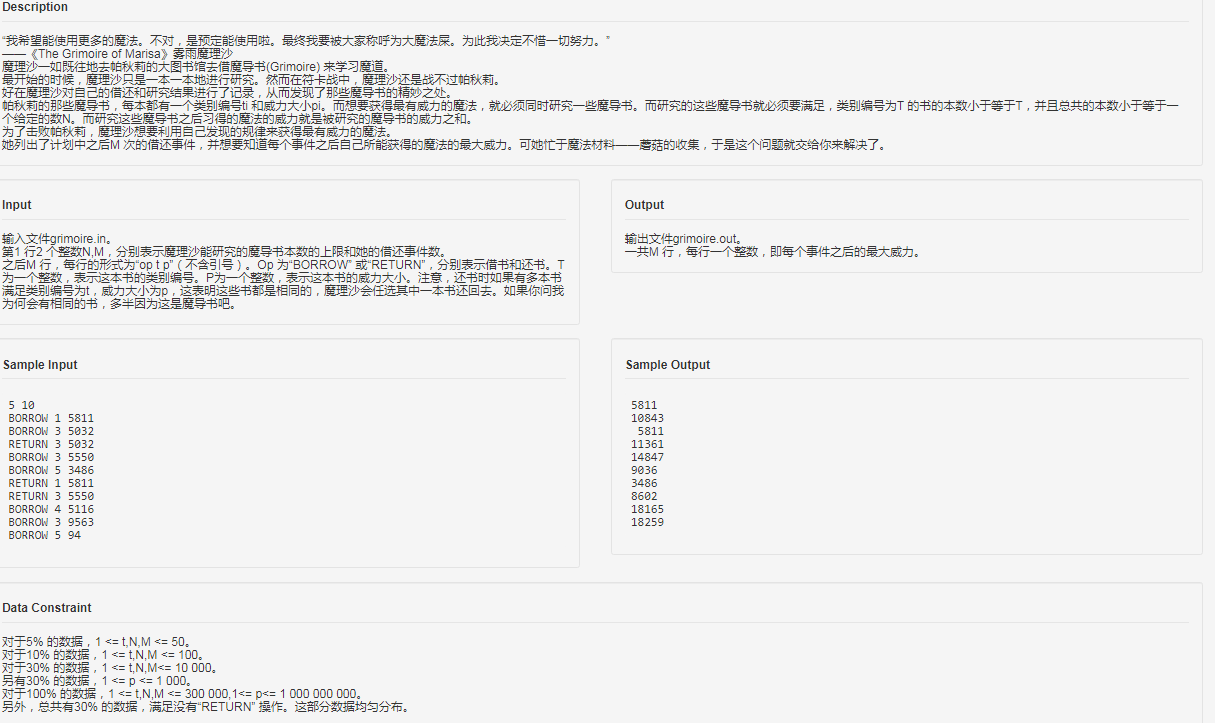
思路

简单的想，就是在 \(T\) 个可重集合每个中选出 \(k\) 个最大的数组成新的可重集合，其中 \(k\) 为其编号

然后在新的集合中选前 \(n\) 大的数，求其和

考虑开 \(T + 1\) 个权值线段树，维护对应的 \(T\) 个可重集合和答案可能在的第 \(T + 1\) 个代表新的集合的线段树

由于空间限制，我们需要动态开点（其实动态开点很简单，线段树二分下去时，遇到一个空节点再使用它。如此一来，在只需开可能使用的节点数）

然后维护区间个数，区间和（注意一个点可能有多个数）

因为是动态开点，所以再记录它的左、右子树的编号

对于 \(B\) 操作，我们直接在根为 \(t\) 的线段树中加入，然后考虑它能不能进入第 \(T + 1\) 棵线段树成为可能的答案。

即查它在第 \(t\) 棵线段树中的从大到小的排名（其实就是求第 \(t\) 棵线段树中 \(p\) 到上限的个数）和）。

如果它的排名 \(\leq t\) ，则可能加入第 \(T + 1\) 个线段树。加入后把现在排名为 \(t+1\) 的数从第 \(T + 1\) 棵线段树中删去（即原先的排名为 \(t\) 的数，它在第 \(T + 1\) 棵线段树中），当然，如果有的话。

对于 \(R\) 操作，就是 \(B\) 操作的逆操作，具体见代码。

\(Code\)

#include<cstdio>
#include<iostream>
using namespace std;
typedef long long LL;

const int N = 3e5 , Len = 1e9;
int n , m , tot , len = N + 1;
LL tr[18000005][5];

inline void New(int t , int x){if (!tr[t][x]) tr[t][x] = ++len;}

inline void update(int t , int l , int r , int p , int v)
{
	tr[t][2] += (LL)v;
	tr[t][3] += (LL)p * v;
	if (l == r) return;
	int mid = (l + r) >> 1;
	if (p <= mid)
	{
		if (!tr[t][0]) New(t , 0);
		update(tr[t][0] , l , mid , p , v);
	}
	else{
		if (!tr[t][1]) New(t , 1);
		update(tr[t][1] , mid + 1 , r , p , v);
	}
}

inline int findk(int t , int l , int r , int x , int y)
{
	if (l >= x && r <= y) return (int)tr[t][2];
	int res = 0 , mid = (l + r) >> 1;
	if (x <= mid && tr[tr[t][0]][2]) res += findk(tr[t][0] , l , mid , x , y);
	if (y > mid && tr[tr[t][1]][2]) res += findk(tr[t][1] , mid + 1 , r , x , y);
	return res;
}

inline int kfind(int t , int l , int r , int k)
{
	if (l == r) return k <= tr[t][2] ? l : 0;
	int mid = (l + r) >> 1;
	if (tr[tr[t][1]][2] < k) return kfind(tr[t][0] , l , mid , k - tr[tr[t][1]][2]);
	else return kfind(tr[t][1] , mid + 1 , r , k);
}

inline LL query(int t , int l , int r , int k)
{
	if (l == r) return 1LL * min(1LL * k , tr[t][2]) * l;
	int mid = (l + r) >> 1;
	LL res = 0;
	if (tr[tr[t][1]][2] <= k)
	{
		res += tr[tr[t][1]][3];
		if (tr[tr[t][0]][2] && k > tr[tr[t][1]][2])
			res += query(tr[t][0] , l , mid , k - tr[tr[t][1]][2]);
	}
	else{
		if (tr[tr[t][1]][2]) res += query(tr[t][1] , mid + 1 , r , k);
	}
	return res;
}

int main()
{
	freopen("grimoire.in" , "r" , stdin);
	freopen("grimoire.out" , "w" , stdout);
	scanf("%d%d" , &n , &m);
	int t , p;
	char op[8];
	for(register int i = 1; i <= m; i++)
	{
		int s1 , s2;
		scanf("%s%d%d" , op , &t , &p);
		if (op[0] == 'B')
		{
			update(t , 1 , Len , p , 1);
			s1 = findk(t , 1 , Len , p , Len);
			if (s1 <= t)
			{
				update(N + 1 , 1 , Len , p , 1);
				s2 = kfind(t , 1 , Len , t + 1);
				if (s2) update(N + 1 , 1 , Len , s2 , -1);
			}
		}
		else{
			s1 = findk(t , 1 , Len , p , Len);
			update(t , 1 , Len , p , -1);
			if (s1 <= t)
			{
				update(N + 1 , 1 , Len , p , -1);
				s2 = kfind(t , 1 , Len , t);
				if (s2) update(N + 1 , 1 , Len , s2 , 1);
			}
		}
		printf("%lld\n" , query(N + 1 , 1 , Len , n));
	}
}