LOJ.数列分块入门3

题目

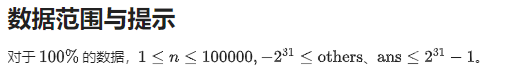
分析

由大题目知此题分块

注意处理前驱下标的合法性

\(Code\)

#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;

const int N = 1e5 + 5;
int n, a[N], t[N], st[N], ed[N], be[N], tag[N];

void Sort(int x)
{
	for(register int i = st[x]; i <= ed[x]; i++) t[i] = a[i];
	sort(t + st[x], t + ed[x] + 1);
}

void prepare()
{
	int num = (int)sqrt(n);
	for(register int i = 1; i <= num; i++) st[i] = n / num * (i - 1) + 1, ed[i] = n / num * i;
	ed[num] = n;
	for(register int i = 1; i <= num; i++)
	{
		for(register int j = st[i]; j <= ed[i]; j++) be[j] = i;
		Sort(i);
	}
}

void update(int l, int r, int c)
{
	int x = be[l], y = be[r];
	if (x == y)
	{
		for(register int i = l; i <= r; i++) a[i] += c;
		Sort(x); return;
	}
	for(register int i = l; i <= ed[x]; i++) a[i] += c;
	for(register int i = st[y]; i <= r; i++) a[i] += c;
	for(register int i = x + 1; i <= y - 1; i++) tag[i] += c;
	Sort(x), Sort(y);
}

int get(int x, int y, int c)
{
	if (!x || !y) return x + y;
	int p = c - t[x] - tag[be[x]], q = c - t[y] - tag[be[y]];
	return (p < q) ? (x) : (y);
}

int query(int l, int r, int c)
{
	int x = be[l], y = be[r], p, q = 0x3f3f3f3f;
	if (x == y)
	{
		for(register int i = l; i <= r; i++)
			if (a[i] + tag[x] < c && c - a[i] - tag[x] < q) q = c - a[i] - tag[x];
		return (q == 0x3f3f3f3f) ? (-1) : (c - q);
	}
	for(register int i = l; i <= ed[x]; i++)
		if (a[i] + tag[x] < c && c - a[i] - tag[x] < q) q = c - a[i] - tag[x];
	for(register int i = st[y]; i <= r; i++)
		if (a[i] + tag[y] < c && c - a[i] - tag[y] < q) q = c - a[i] - tag[y];
	for(register int i = x + 1; i <= y - 1; i++)
	{
		p = lower_bound(t + st[i], t + ed[i] + 1, c - tag[i]) - t - 1;
		if (p < st[i]) continue;
		if (c - t[p] - tag[i] < q) q = c - t[p] - tag[i];
	}
	return (q == 0x3f3f3f3f) ? (-1) : (c - q);
}

int main()
{
	scanf("%d", &n);
	for(register int i = 1; i <= n; i++) scanf("%d", &a[i]);
	prepare();
	for(register int i = 1, opt, l, r, c; i <= n; i++)
	{
		scanf("%d%d%d%d", &opt, &l, &r, &c);
		if (opt == 0) update(l, r, c);
		else printf("%d\n", query(l, r, c));
	}
}