LeetCode - 二维数组及滚动数组

1. 二维数组及滚动数组总结

在二维数组num[i][j]中，每个元素都是一个数组。有时候，二维数组中的某些元素在整个运算过程中都需要用到；但是有的时候我们只需要用到前一个或者两个数组，此时我们便可以用几个数组来代替原来的二维数组来降低空间消耗。这个思维就是：滚动数组。

滚动数组就是使用k个一维数组来保存原来二维数组的后k个数组，在使用的过程中通过不断更新这k个数组来达到与二维数组相同的效果。

注意：滚动数组的目的是：减少空间消耗；滚动数组能够使用的前提是：每次处理时不需要访问二维数组中的所有元素，只与当前处理元素的前一个或两个数组有关，如：num[i][j] = num[i-1][j] + num[i-2][j]类似情况，我们就可以使用滚动数组。

滚动数组在动态规划过程中经常使用，此处我们先提前了解一下。

2. 题目记录

118. 杨辉三角

分析题意

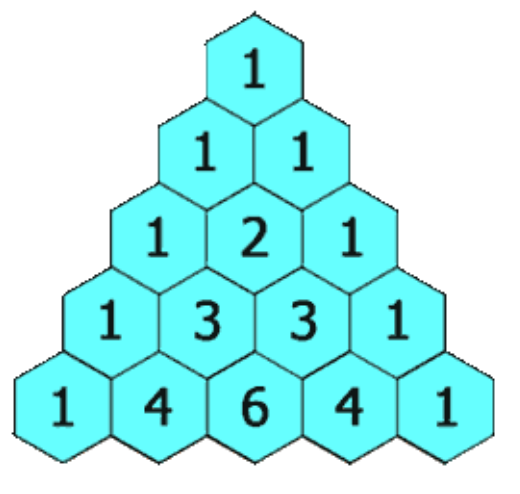
给定一个非负整数 numRows，生成「杨辉三角」的前 numRows行。在「杨辉三角」中，每个数是它左上方和右上方的数的和。

思路分析

关键在于理解：杨辉三角是如何生成的。即：对于第i行元素来说，除了第一个和最后一个，对于任意一个元素 j都有nums[i][j] = nums[i-1][j-1] + nums[i-1][j]

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> ans = new ArrayList<>();

        for(int row = 1; row <= numRows; row++){
            List<Integer> temp = new ArrayList<Integer>();
            for(int col = 1; col <= row; col++){
                if(col == 1 || col == row){
                    temp.add(1);
                }else{
                    // row - 1 对应的idx 为 row-1-1
                    List<Integer> pre = ans.get(row - 2);
                    // col 对应的idx为col-1
                    temp.add(pre.get(col-2) + pre.get(col-1));
                }
            }

            ans.add(temp);
        }
        return ans;
    }
}

复杂度分析

时间复杂度：\(O(n^{2})\)

空间复杂度：\(O(1)\) 返回值所占空间不考虑

119. 杨辉三角 II

分析题意

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。在「杨辉三角」中，每个数是它左上方和右上方的数的和。

思路分析

这个题和上一道题很相似，区别在于：本题只需要返回指定行的结果。根据题意知道，第i行的数据只与第i-1行的数据有关系，所以我们可以使用滚动数组来将二维数组压缩为两个数组。

class Solution {
    public List<Integer> getRow(int rowIndex) {
        int[] pre = new int[rowIndex + 1];
        int[] cur = new int[rowIndex + 1];

        for(int idx = 0; idx <= rowIndex; idx++){
            for(int j = 0; j < idx + 1; j++){
                if(j == 0 || j == idx){
                    cur[j] = 1;
                }else{
                    cur[j] = pre[j-1] + pre[j];
                }
            }
            int[] temp = pre;
            pre = cur;
            cur = temp;
        }

        List<Integer> ans = new ArrayList<>();
        for(int i = 0; i < pre.length; i++){
            ans.add(pre[i]);
        }
        return ans;
    }
}

复杂度分析

时间复杂度：\(O(n^2)\)

空间复杂度：\(O(n)\)，通过滚动数组，我们将空间消耗从\(O(n^{2})\)降为了\(O(n)\)。

扩展

其实这道题可以继续优化，如果不考虑返回数据占用的空间，这道题可以做到O(1)的空间复杂度。

做到O(1)空间复杂度的思路就是：将上述两个数组合并为一个数组，关键问题就是怎么才能复用这个数组呢？

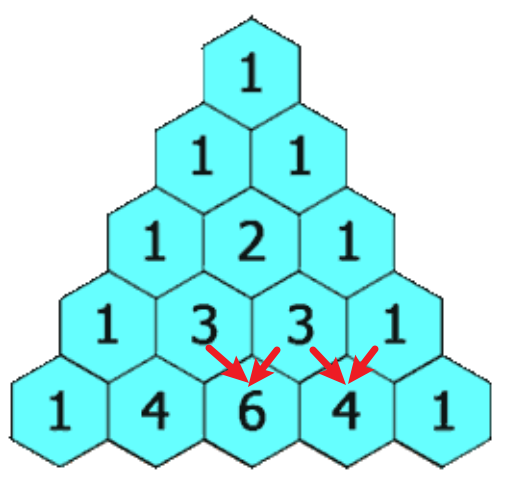
我们直接创建一个大小为n的ans数组，假定我们想要第4行的数据，而我们已经遍历过第3行，那么此时ans数组中的元素为：

[1, 3, 3, 1, 0]

如果我们从前到后遍历，那么在遍历到j=2时，数组被更新为：

[1, 4, 3, 1, 0]

那么此时计算j=3时，j=2位置的元素已经被覆盖为第4行的新数据，而不是第3行的旧数据。所以我们不能从做左到右进行遍历。我们再思考一下，第j个元素的更新依赖于j-1和j元素，只更新j元素，所以我们可以从后向前遍历！

从后向前遍历防止之前元素被覆盖的思路在背包问题中也有体现。

class Solution {
    public List<Integer> getRow(int rowIndex) {
       List<Integer> ans = new ArrayList<>();

       for(int i = 0; i <= rowIndex; i++){
           ans.add(1);
       }

       for(int idx = 2; idx <= rowIndex; idx++){
           // 从后往前遍历，防止前一层的元素被覆盖掉
           for(int j = idx; j >=0; j--){
               if(j == idx || j == 0){
                   // 第idx行的第1个和最后1个元素为1，不需要修改
                   continue;
               }else{
                   ans.set(j, ans.get(j) + ans.get(j-1));
               }
           }
       }
       return ans;
    }
}

661. 图片平滑器

分析题意

注意：3x3滑动窗内的9个数字的平均值，需要向下取整。还需要注意的一点就是：如果个数小于9个，那么求平均值的时候应该除以真正的数字的数目，而不是除以9。

思路分析

按照题意进行滑动窗的模拟操作。

对于(i, j)坐标，它周围的8个坐标分布如下：

(i-1, j-1)  (i-1, j)  (i-1, j+1)
(i, j-1)    (i, j)    (i, j+1)
(i+1, j-1)  (i+1, j)  (i+1, j+1)

class Solution {
    public int[][] imageSmoother(int[][] img) {
        int[][] ans = new int[img.length][img[0].length];

        for(int i = 0; i < img.length; i++){
            for(int j = 0; j < img[0].length; j++){
                ans[i][j] = getAverage(img, i, j);
            }
        }

        return ans;
    }

    int getAverage(int[][] img, int i, int j){
        int sum = 0;
        int num = 0;
				// i - 1 层
        if(i - 1 >= 0){
            if(j - 1 >= 0){
                sum += img[i-1][j-1];
                num++;
            }

            sum += img[i-1][j];
            num++;

            if(j + 1 < img[0].length){
                sum += img[i-1][j+1];
                num++;
            }
        }

        if(j - 1 >= 0){
            sum += img[i][j-1];
            num++;
        }

        sum += img[i][j];
        num++;

        if(j + 1 < img[0].length){
            sum += img[i][j + 1];
            num ++;
        }

				// i + 1 层
        if(i + 1 < img.length){
            if(j - 1 >= 0){
                sum += img[i + 1][j - 1];
                num ++;
            }

            sum += img[i + 1][j];
            num ++;

            if(j + 1 < img[0].length){
                sum += img[i + 1][j + 1];
                num ++;
            }
        }

        return sum / num;

    }
}

简化的代码如下：

class Solution {
    int[] row = {-1, -1, -1, 0, 0, 0, 1, 1, 1};
    int[] col = {-1, 0, 1, -1, 0, 1, -1, 0, 1};
    public int[][] imageSmoother(int[][] img) {
        int[][] ans = new int[img.length][img[0].length];

        for(int i = 0; i < img.length; i++){
            for(int j = 0; j < img[0].length; j++){
                ans[i][j] = getAverage(img, i, j);
            }
        }

        return ans;
    }

    int getAverage(int[][] img, int i, int j){
        int sum = 0;
        int num = 0;
        for(int idx = 0; idx < 9; idx++){
						// 判断坐标是否合法
            if(i + row[idx] >= 0 && i + row[idx] < img.length && j + col[idx] >= 0 && j + col[idx] < img[0].length){
                sum += img[i + row[idx]][j + col[idx]];
                num ++;
            }
        }
        return sum / num;

    }
}

复杂度分析

时间复杂度：\(O(n^2)\)

空间复杂度：\(O(1)\) 返回数组占用空间不计入

598. 范围求和 II

分析题意

注意关键词：初始化时所有的 0 ，也就是说所有数值在操作之前都是0。

思路分析

这道题看似是需要创建一个二维数组，然后一次一次模拟操作，最后遍历查出最大的数据的个数。其实，并不需要这样。我们想一下：因为二维数组初始化时都是0，所以在所有操作完成之后，二维数组中每个单元格内的数字其实就是有多少个操作包含了这个单元格。又因为所有操作都是从(0, 0)开始的，所以我们要求最大的整数出现的频次，那其实就是求：所有操作的的最小交集。

class Solution {
    public int maxCount(int m, int n, int[][] ops) {
        int a = m;
        int b = n;
        for(int i = 0; i < ops.length; i++){
            a = Math.min(a, ops[i][0]);
            b = Math.min(b, ops[i][1]);
        }
        return a  * b;
    }
}

复杂度分析

时间复杂度：\(O(n)\)

空间复杂度：\(O(1)\)

419. 甲板上的战舰

分析题意

这道题就是一道语文题，能不能做出来完全取决于你有没有理解题目在说什么。

首先，明确一个：题目是要统计board上的军舰数量，而不是要你计算军舰的数量。我第一次做的时候就是以为要模拟计算军舰的数量，所以一直没有做出来。

其次，要明确战舰的定义，战舰或者是横着摆放或者是竖着摆放。也就是说一个战舰，他要么占一行的很多列，要么站一列的很多行；不可能同时占用很多行和很多列。

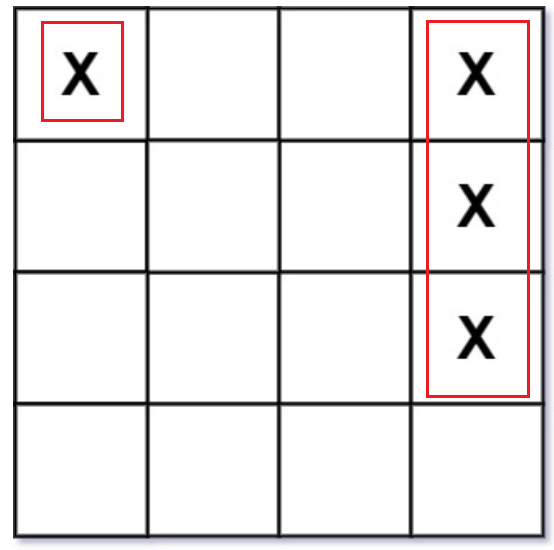
上述两个红框就是两个战舰，所以此时答案为2。

思路分析

其实我们只需要找到战舰的头就可以了，那么战舰的头怎么寻找呢？其实就是它的左侧和上侧都没有战舰，那么这个战舰一定是战舰头部。

class Solution {
    public int countBattleships(char[][] board) {
        int ans = 0;
        for(int i = 0; i < board.length; i++){
            for(int j = 0; j < board[0].length; j++){
                // 此处有战舰
                if(board[i][j] == 'X'){
                    boolean flag = true;
                    if(i - 1 >= 0 && board[i-1][j] != '.'){
                        flag = false;
                    }

                    if(j - 1 >= 0 && board[i][j-1] != '.'){
                        flag = false;
                    }

                    if(flag){
                        ans++;
                    }
                }
            }
        }
        return ans;
    }
}

复杂度分析

时间复杂度：\(O(m \times n)\)

空间复杂度：\(O(1)\)