[排序算法] 堆排序 (C++)

堆排序解释

什么是堆

堆 heap 是一种近似完全二叉树的数据结构，其满足一下两个性质

1. 堆中某个结点的值总是不大于(或不小于)其父结点的值；
2. 堆总是一棵完全二叉树

将根结点最大的堆叫做大根堆(大项堆)，根结点最小的堆叫做小根堆(小项堆)。

堆排序原理

我们一般用大根堆对数组进行正向排序喔

首先将当前的无序数组构成一个无序堆，对于每个元素在堆中对应的下标，由二叉树数组表示法可得

若一个节点的下标为 i，那么其左孩子节点下标为 2 * i + 1，右孩子节点下标为 2 * i + 2。

然后我们再将当前的无序堆进行不断调整，直到最后构造成 大根堆。

之后交换首尾元素，即将当前堆顶的最大元素交换到末尾，这时此元素就完成了归位。

交换完首尾元素后，此时的堆再次变成一个无序堆，需要再次堆对剩余元素进行调整，使其重新变成 大根堆。

重复上述的操作，直至堆的大小为 1，最后所有的元素都交换结束，即完成了堆排序。

---

堆排序动态演示

我们以 [4,7,3,1,6,2,5] 为例进行动态演示

构成无序堆

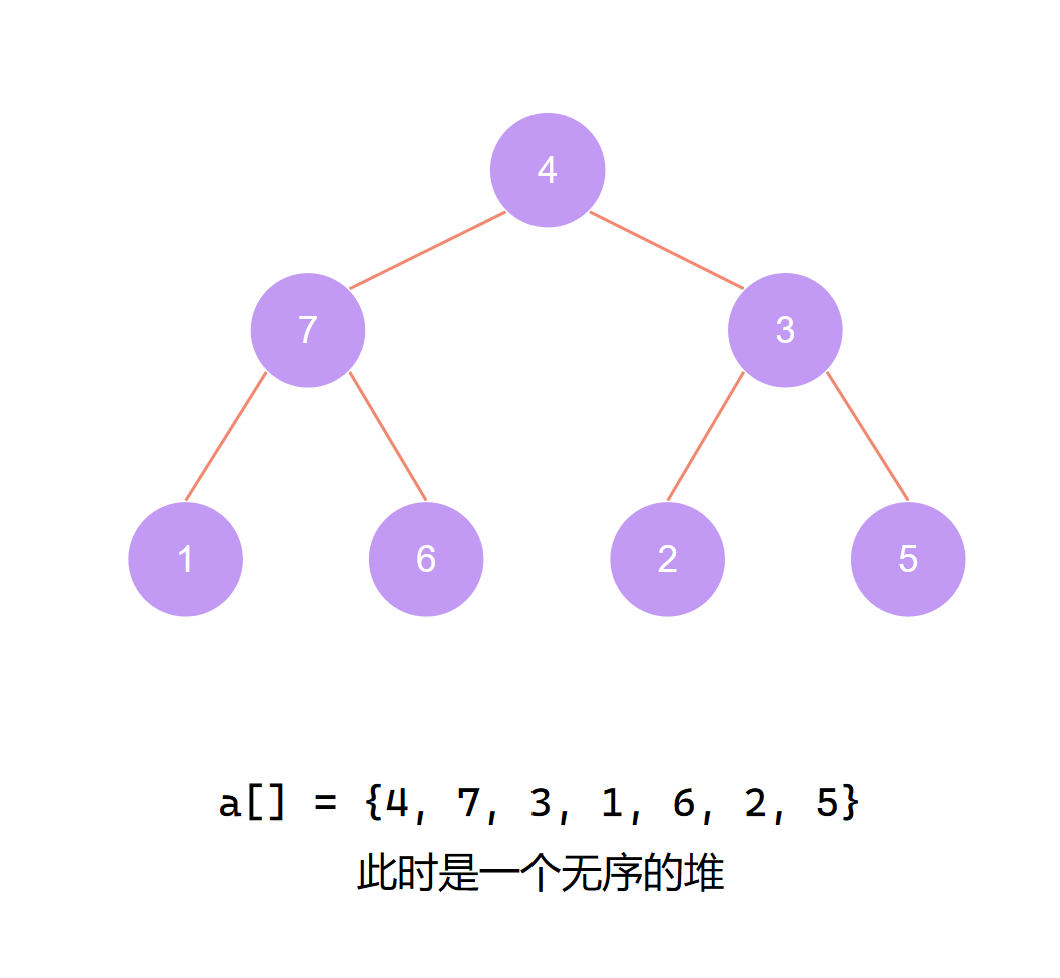
从最后一个非叶子节点开始 调整堆

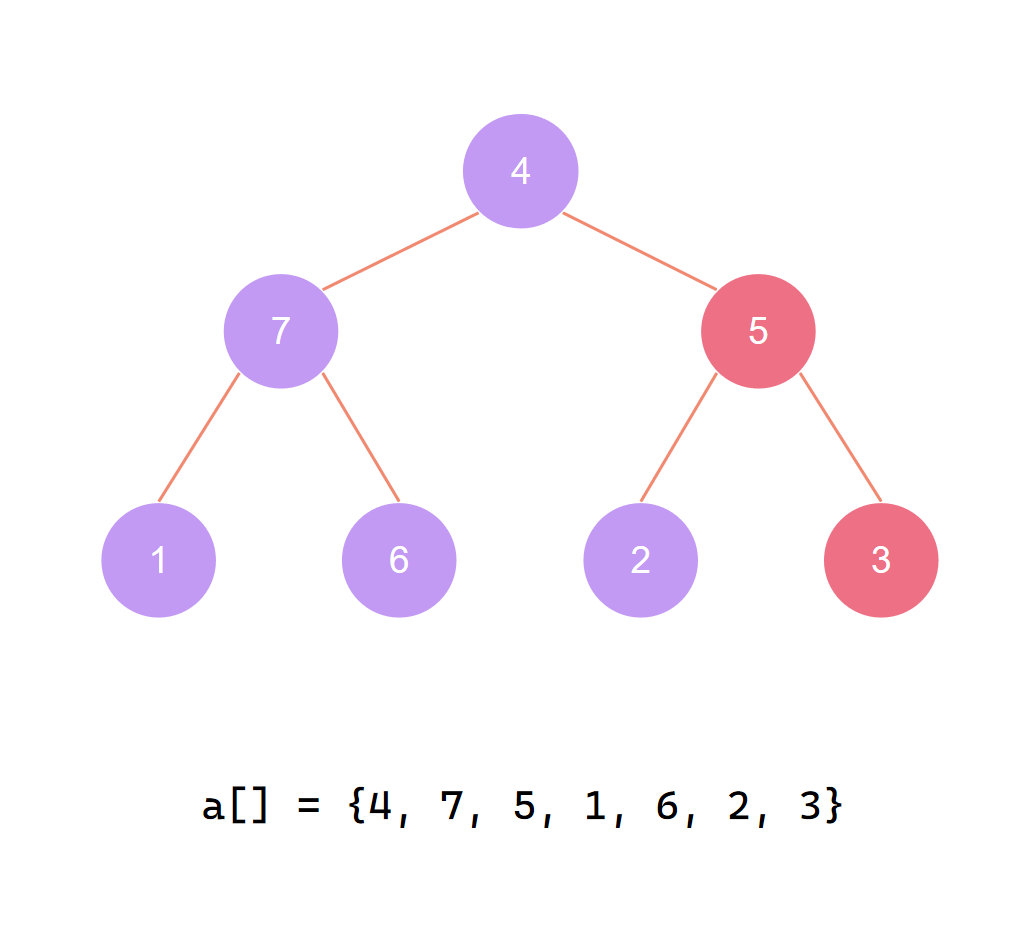
对倒数第二个非叶子节点 调整堆 此时我们发现无需调整

对最后一个非叶子节点 调整堆

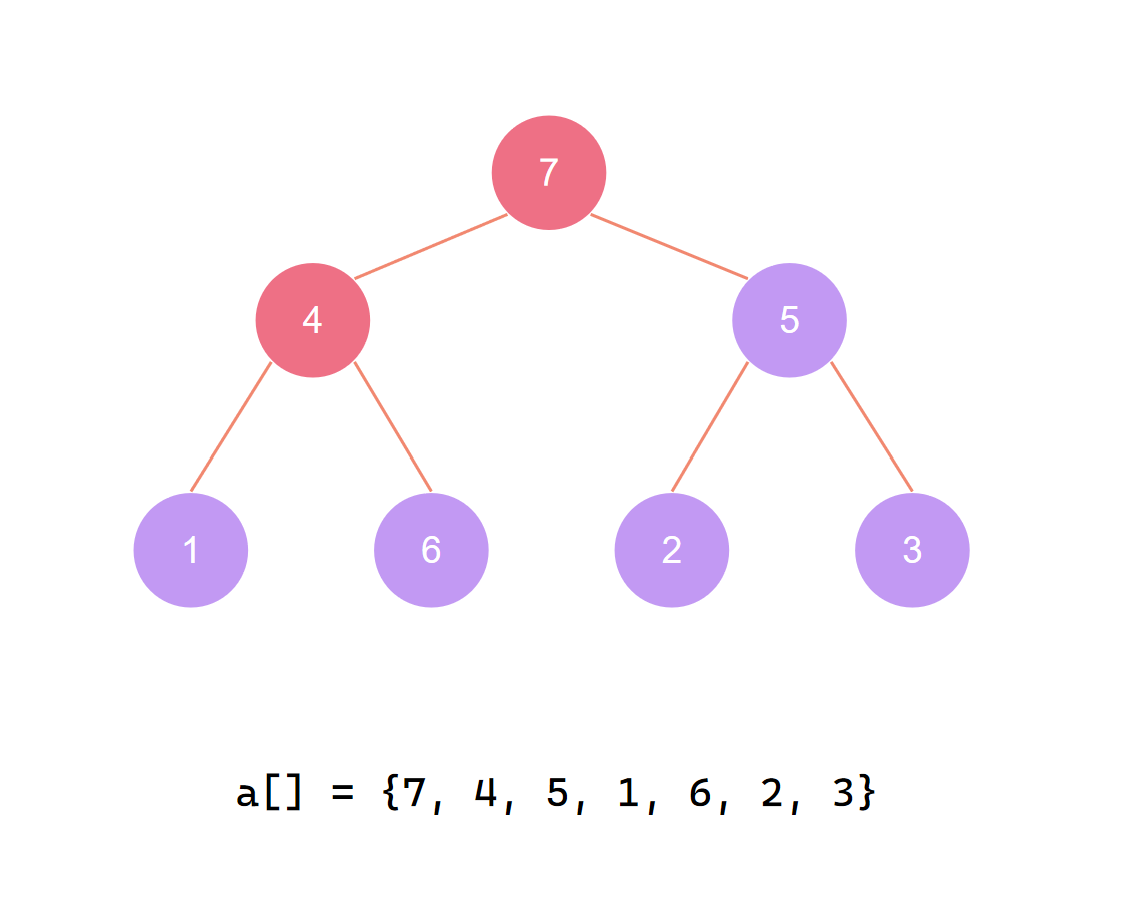
这时当前根节点的左节点由于调整不满足大根堆性质 需递归调整

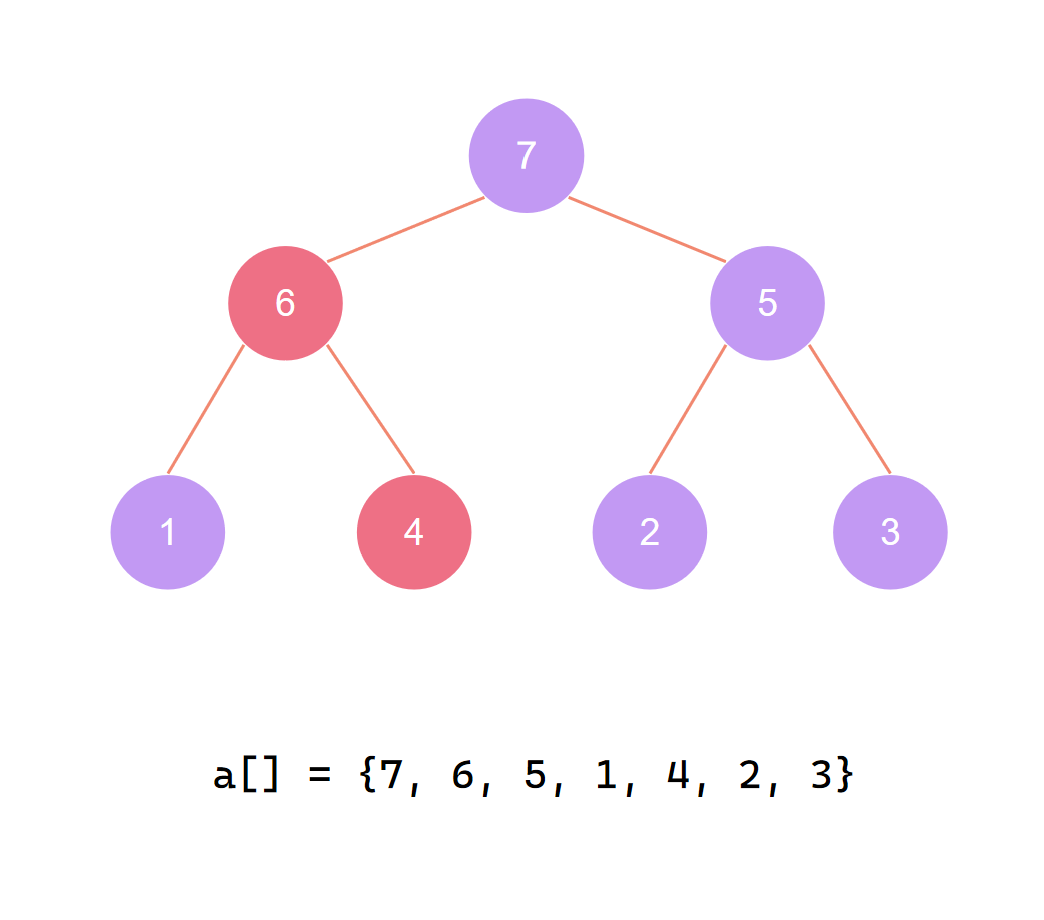
大根堆构建完成

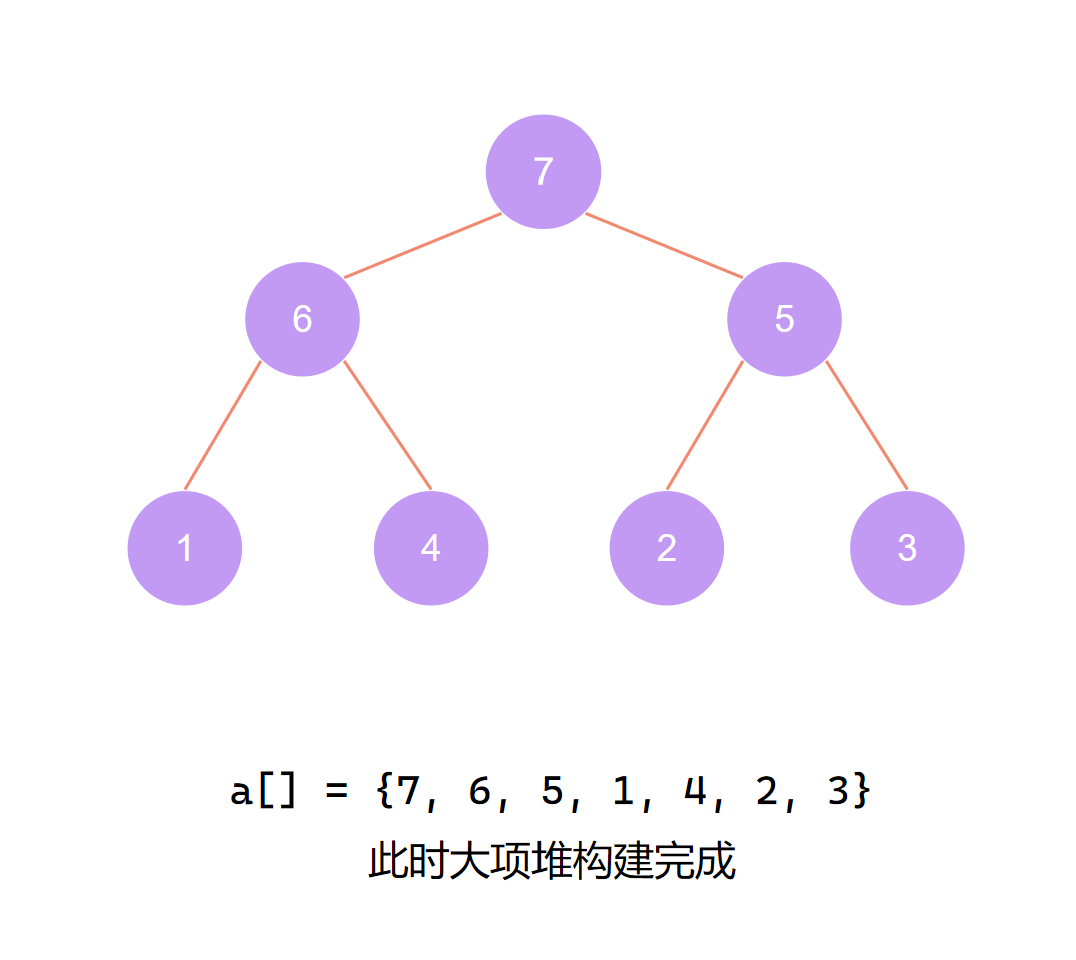
交换首尾 第一个元素归位

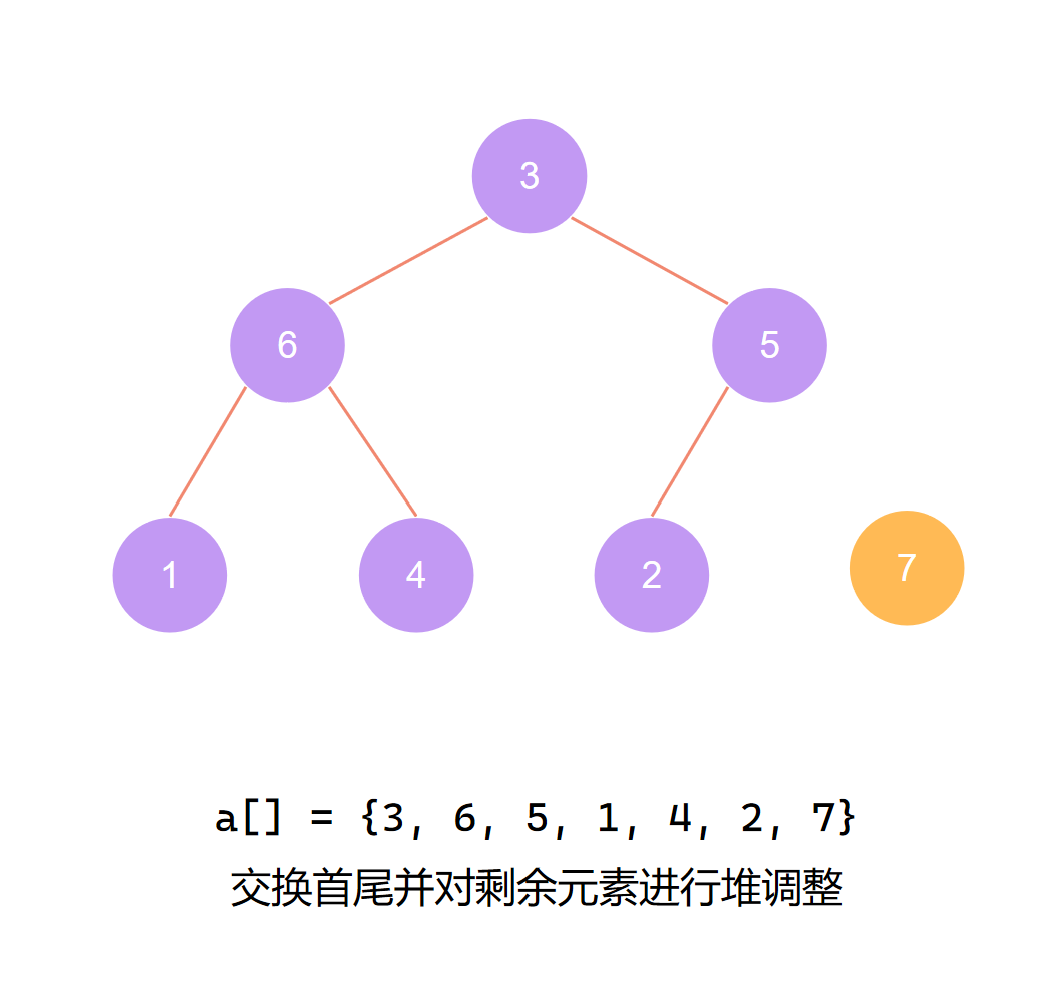
第一个元素归位后 再度调整(1)

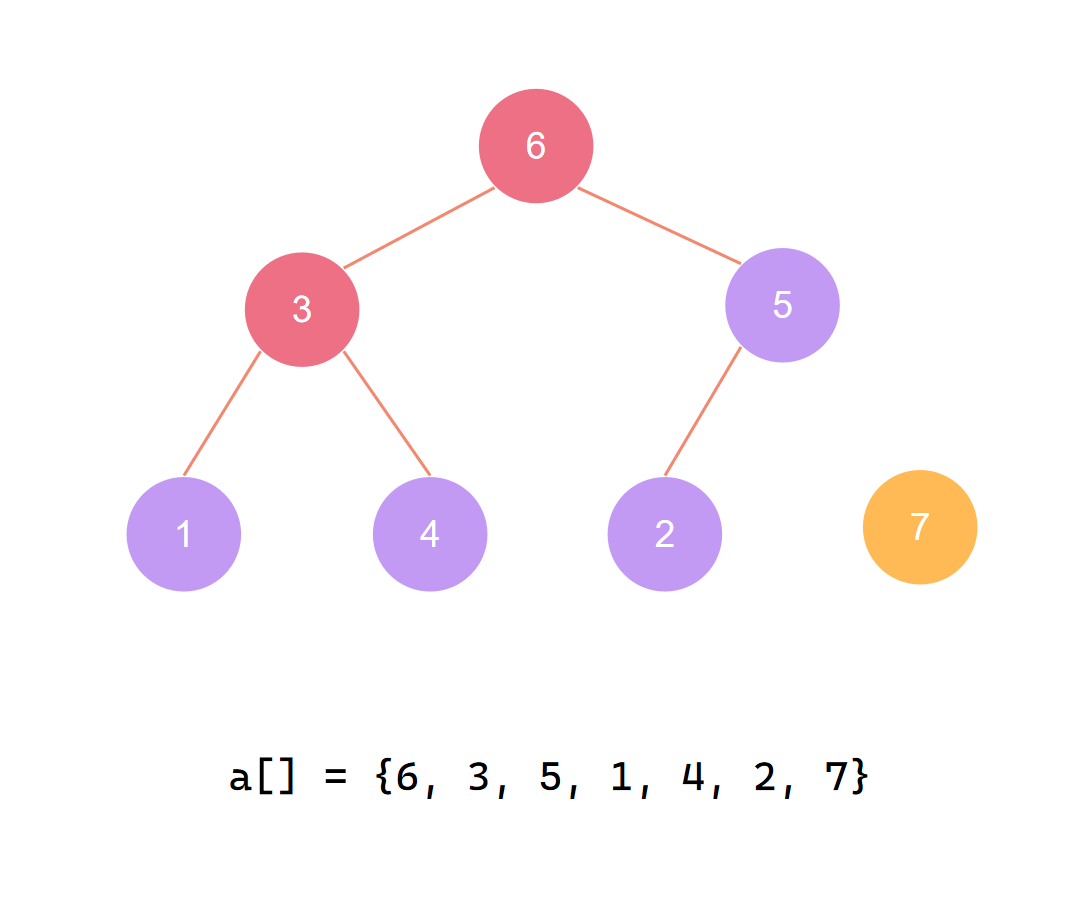
第一个元素归位后 再度调整(2)

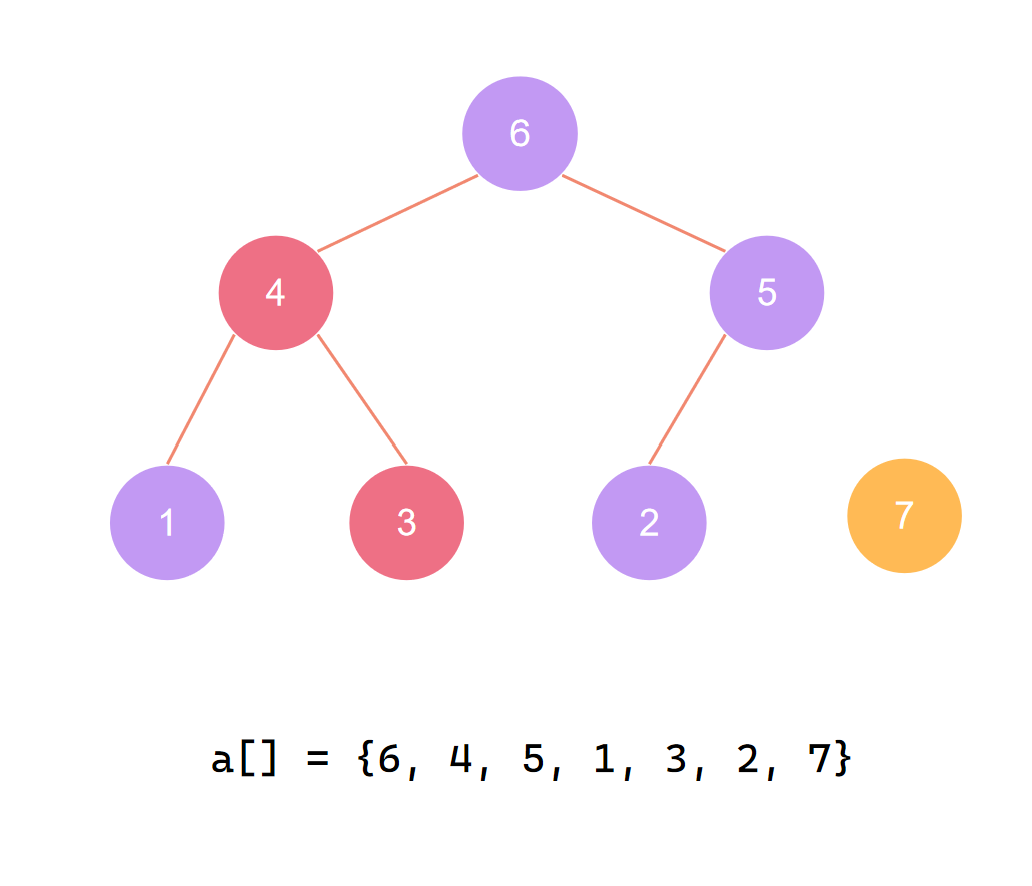
交换首尾 第二个元素归位

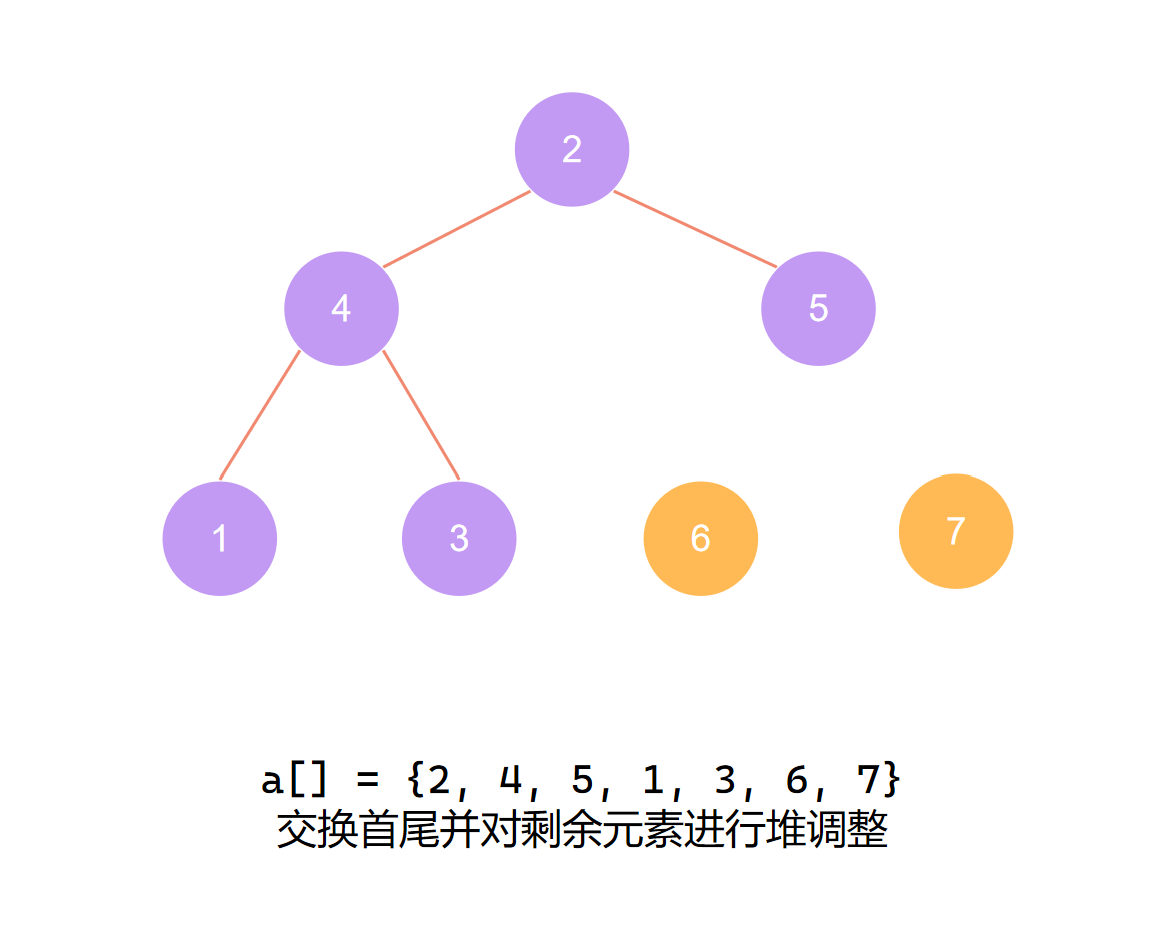
第二个元素归位后 再度调整

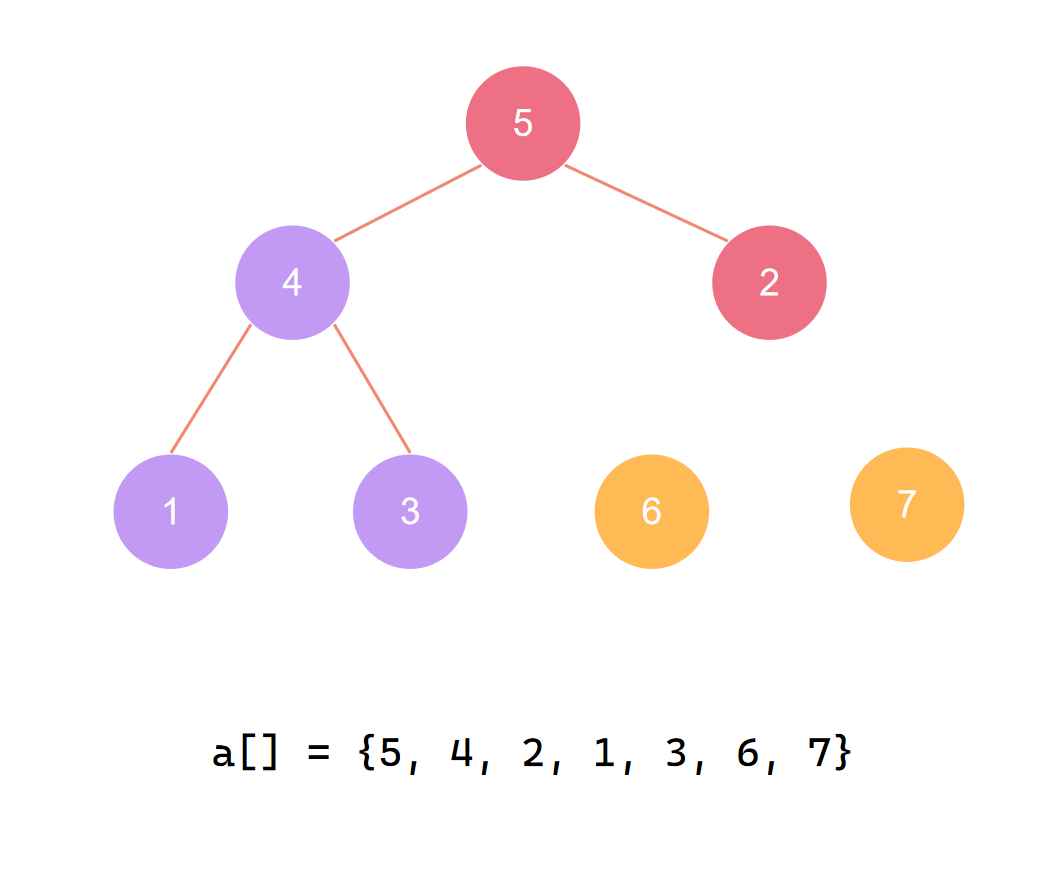
交换首尾 第三个元素归位

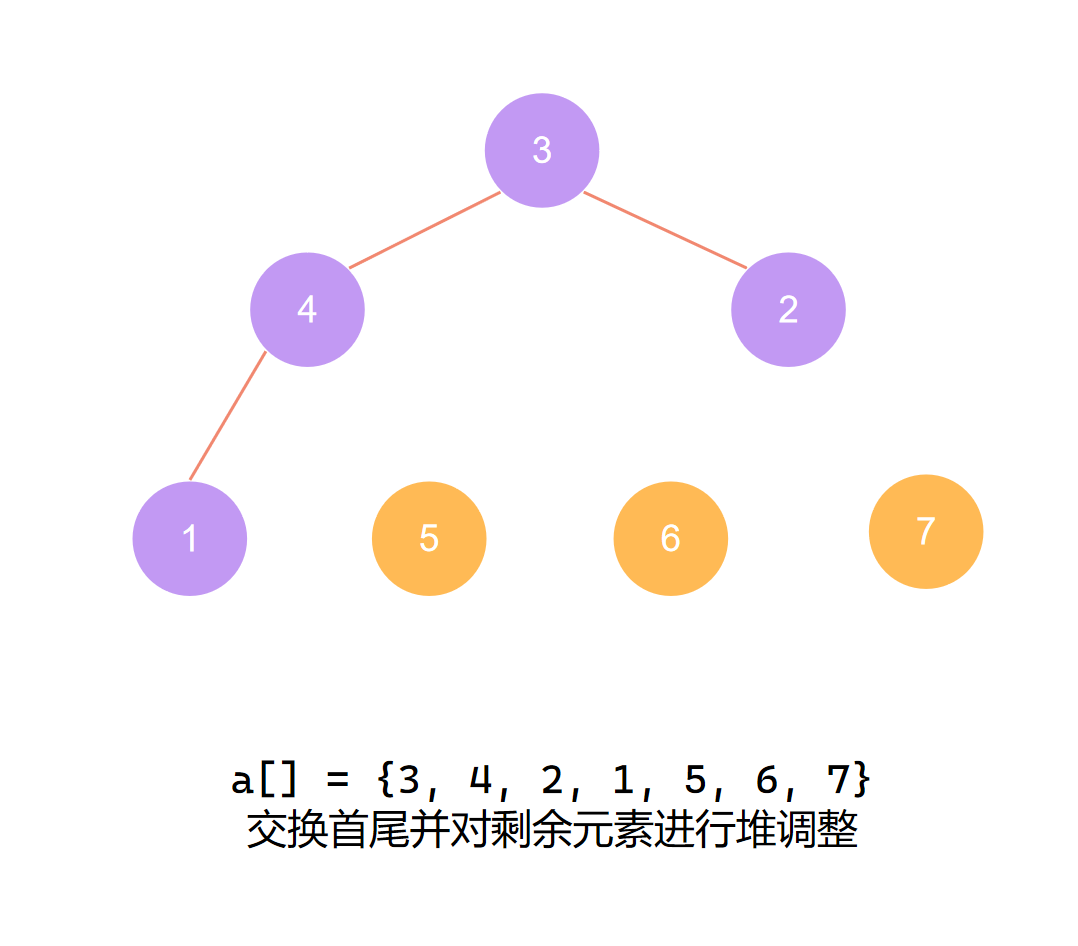
第三个元素归位后 再度调整

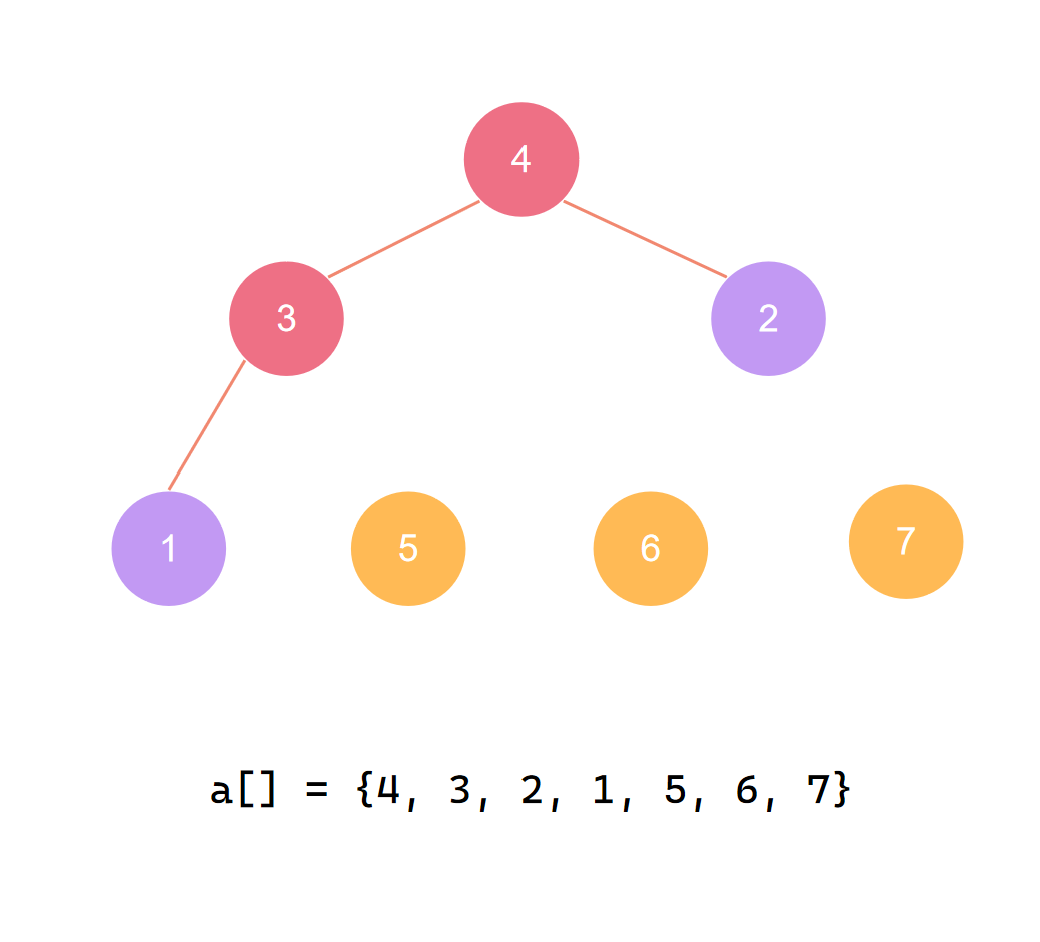
交换首尾 第四个元素归位

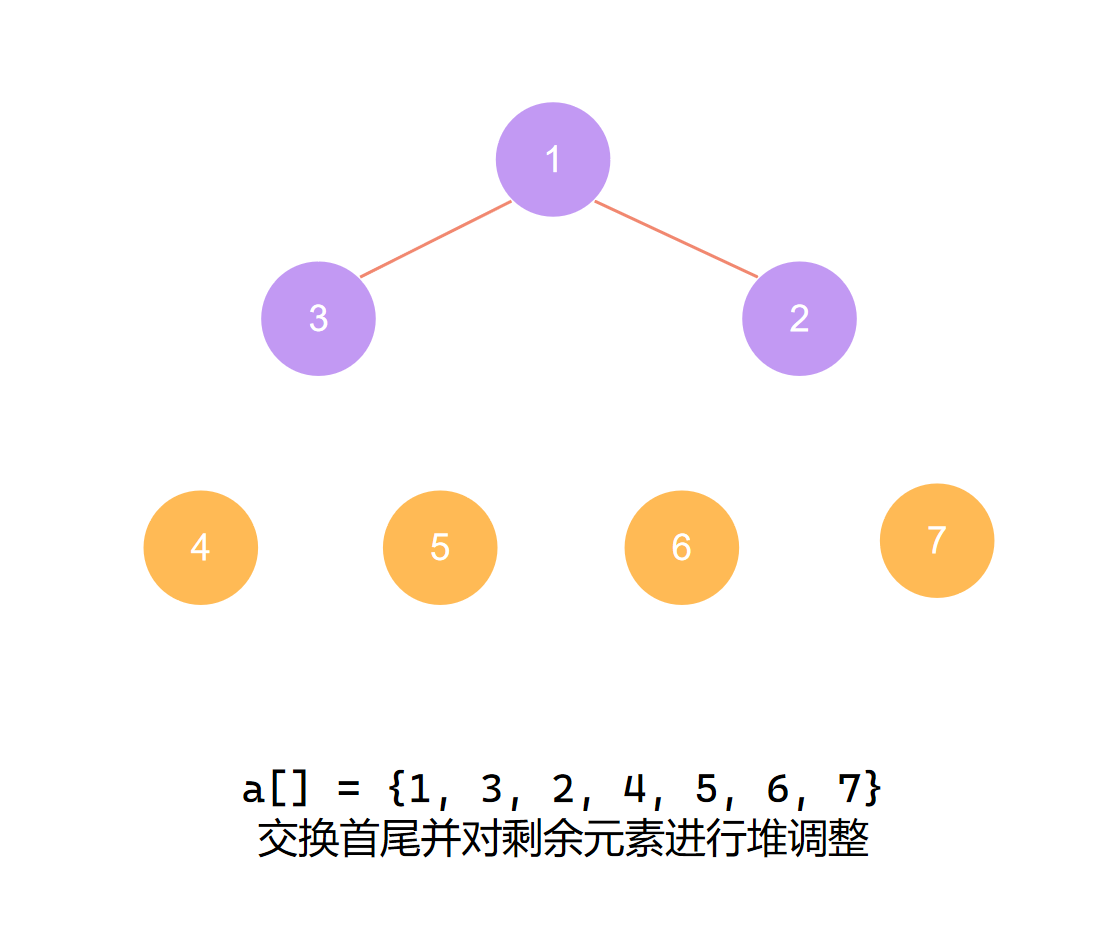
第四个元素归位后 再度调整

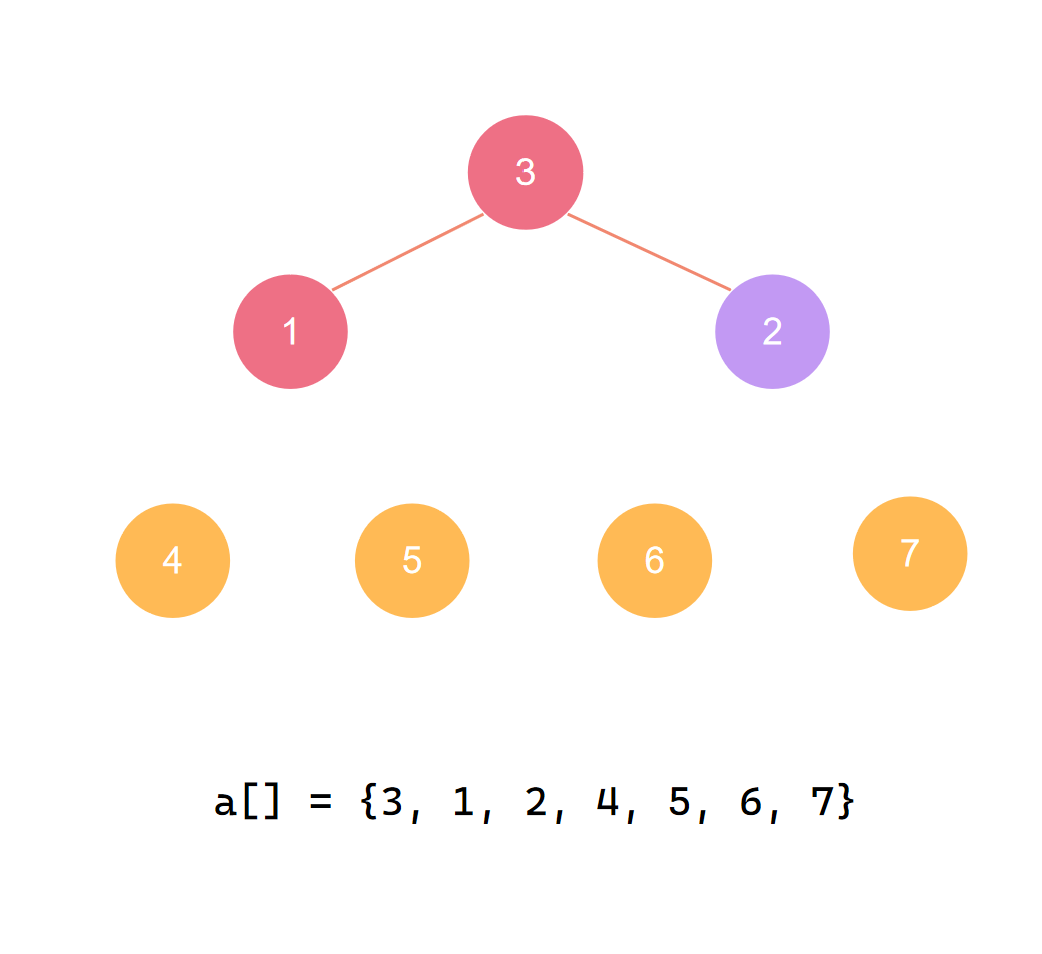
交换首尾 第五个元素归位

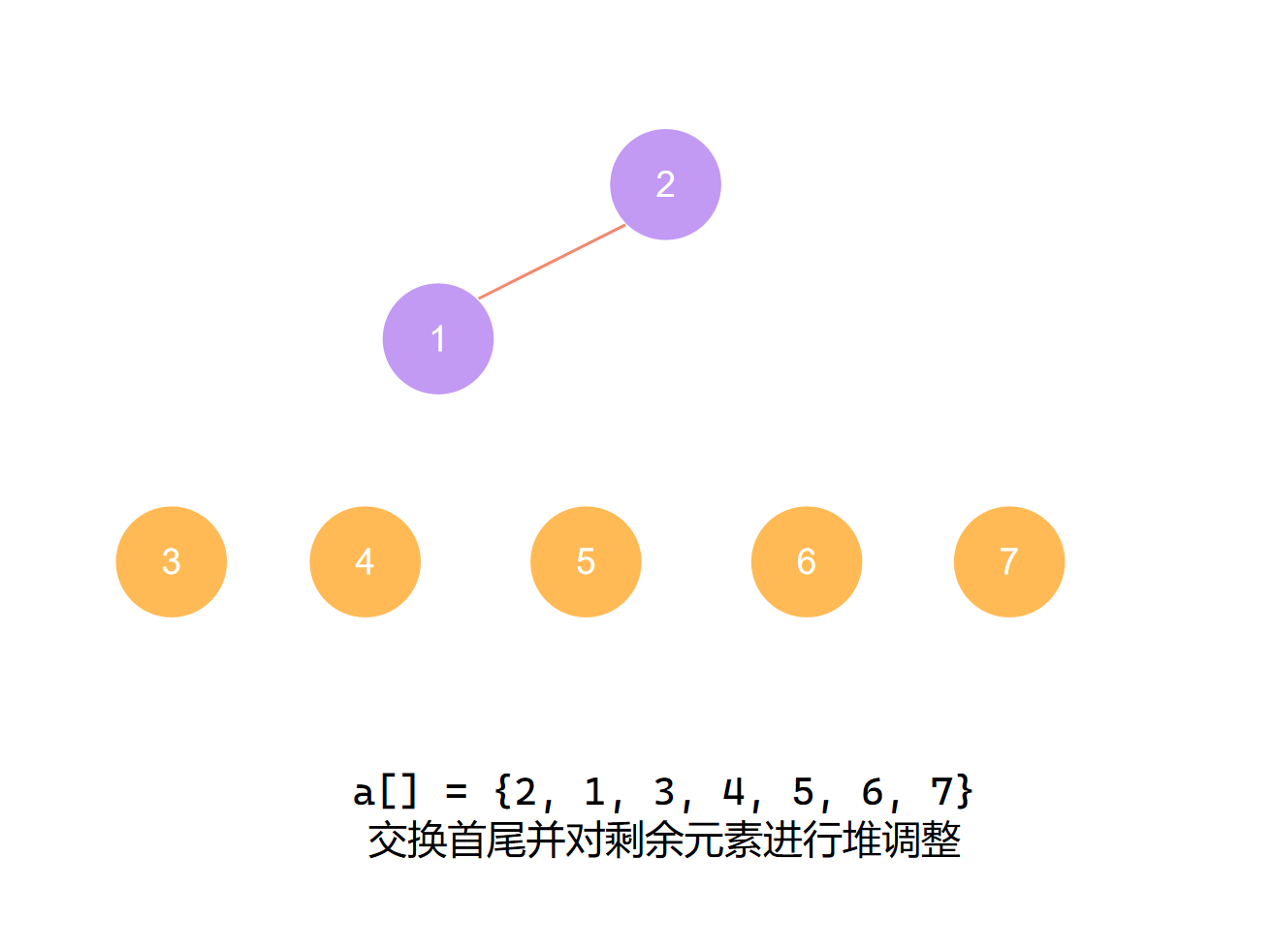
交换首尾 第六个元素归位

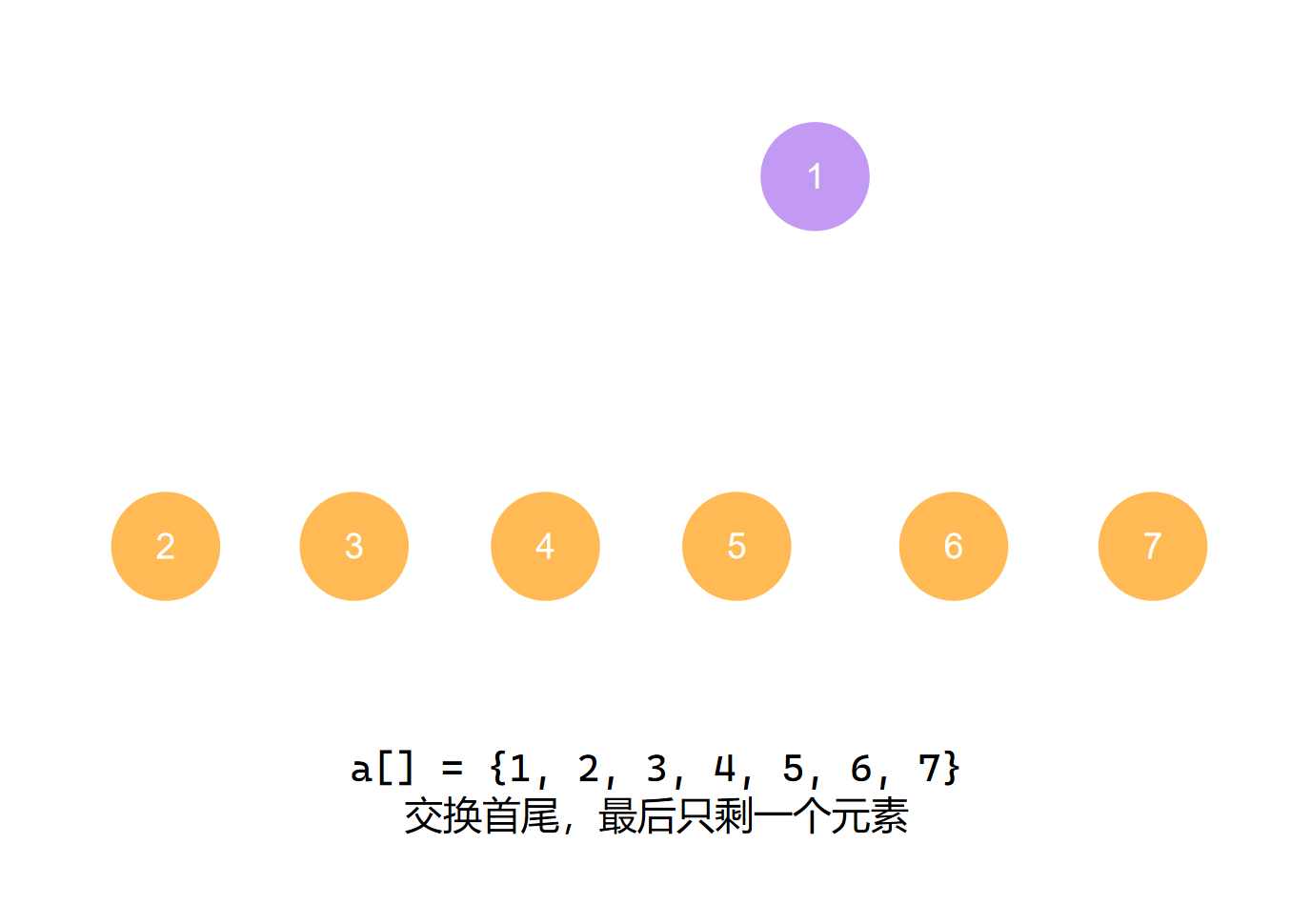
最后堆大小为1，排序完成

---

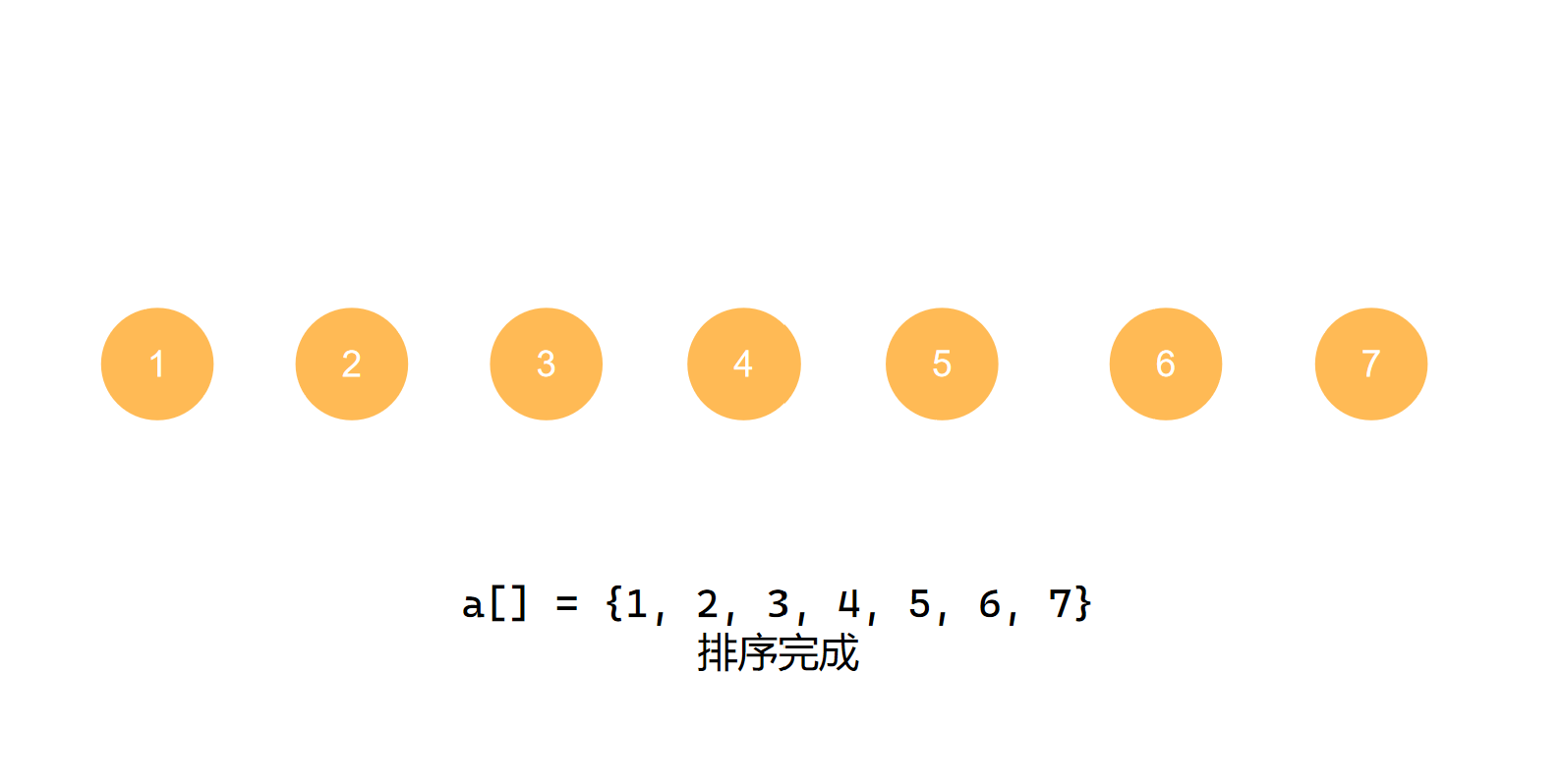
堆排序时间复杂度

构建初始的大根堆时间复杂度为O(n)，

交换及重建大顶堆的过程中，需要交换n-1次，重建大顶堆的过程根据完全二叉树，log2(n-1),log2(n-2)...1 近似为nlogn。

---

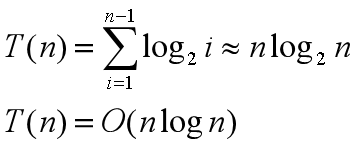
堆排序核心代码

//调整堆
void Heapify(vector<int> &v, int i, int len){
    int left = 2 * i + 1, right = 2 * i + 2;  //二叉树当前节点的左右节点的索引
    int maxindex = i;                         //先默认i为最大值索引 即当前非叶子节点

    if(left < len && v[left] > v[maxindex])   //如果有左节点且左节点值更大
	maxindex = left;
    if(right < len && v[right] > v[maxindex]) //如果有右节点且右节点值更大
	maxindex = right;

    if(maxindex != i){
	//发现最大值并非当前非叶子节点，则需调整 即交换最大值到非叶子节点处
	swap(v[i], v[maxindex]);
	//互换之后，子节点值发生变化，子节点若也有其子节点，则需继续调整其子结构
	Heapify(v, maxindex, len);            //递归 调整堆
    }
}

//无序数组 构建大根堆
void BuildMaxHeap(vector<int> &v, int len){
    //从最后一个非叶子节点开始遍历，调整每个子结构，构建形成大根堆
    for(int i = len / 2 - 1; i >= 0; i--)
	Heapify(v, i, len);
}

//堆排序
void HeapSort(vector<int> &v){
    int len = v.size();
    BuildMaxHeap(v, len);           //构建大根堆
    while(len > 1){
	swap(v[0], v[len - 1]);     //交换首尾数据  尾部最大 且出现在合适位置
	Heapify(v, 0, --len);       //重置大根堆
    }
}

---

完整程序源代码

#include<iostream>
#include<vector>
#include<ctime>
using namespace std;

//调整堆
void Heapify(vector<int> &v, int i, int len){
    int left = 2 * i + 1, right = 2 * i + 2;  //二叉树当前节点的左右节点的索引
    int maxindex = i;                         //先默认i为最大值索引 即当前非叶子节点

    if(left < len && v[left] > v[maxindex])   //如果有左节点且左节点值更大
	maxindex = left;
    if(right < len && v[right] > v[maxindex]) //如果有右节点且右节点值更大
	maxindex = right;

    if(maxindex != i){
	//发现最大值并非当前非叶子节点，则需调整 即交换最大值到非叶子节点处
	swap(v[i], v[maxindex]);
	//互换之后，子节点值发生变化，子节点若也有其子节点，则需继续调整其子结构
	Heapify(v, maxindex, len);            //递归 调整堆
    }
}

//无序数组 构建大根堆
void BuildMaxHeap(vector<int> &v, int len){
    //从最后一个非叶子节点开始遍历，调整每个子结构，构建形成大根堆
    for(int i = len / 2 - 1; i >= 0; i--)
	Heapify(v, i, len);
}

//堆排序
void HeapSort(vector<int> &v){
    int len = v.size();
    BuildMaxHeap(v, len);           //构建大根堆
    while(len > 1){
	swap(v[0], v[len - 1]);     //交换首尾数据  尾部最大 且出现在合适位置
	Heapify(v, 0, --len);       //重置大根堆
    }
}

//打印数据
void show(vector<int> &v){
	for(auto &x : v)
		cout<<x<<" ";
	cout<<endl;
}

main(){
    vector<int> v;
    srand((int)time(0));
    int n = 50;
    while(n--)
	v.push_back(rand() % 100 + 1);
    show(v);
    HeapSort(v);
    cout<<endl<<endl;
    show(v);
}

---

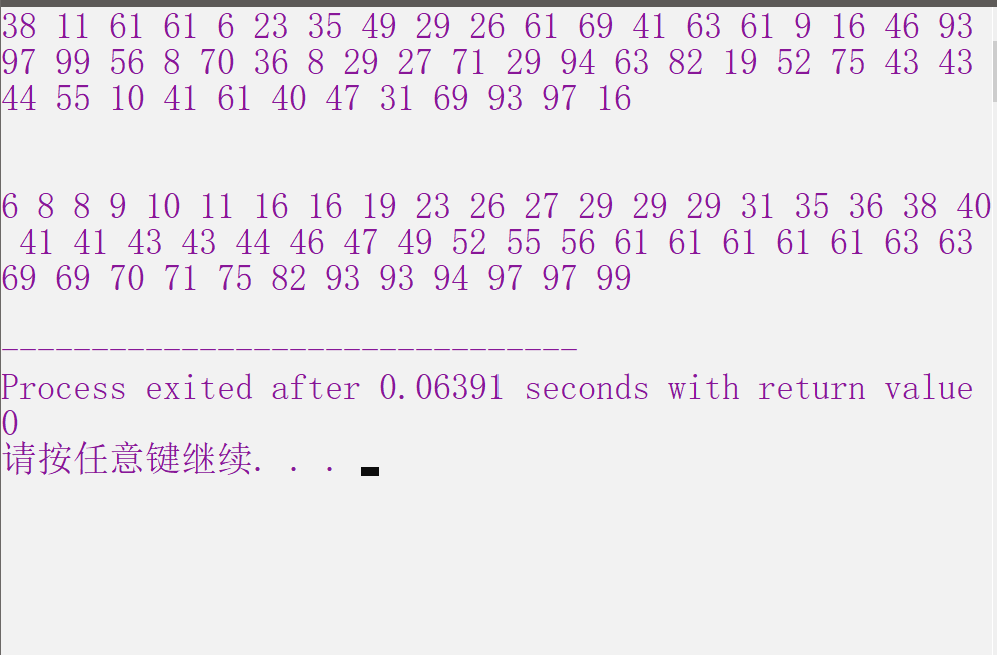
程序运行结果图