Luogu P2619 [国家集训队2]Tree I 凸优化，wqs二分

新学的科技。设\(f(x)\)为选\(x\)条白色边的时候的最小生成树权值和，那么可以猜到它应该是一个下凸函数的形式。

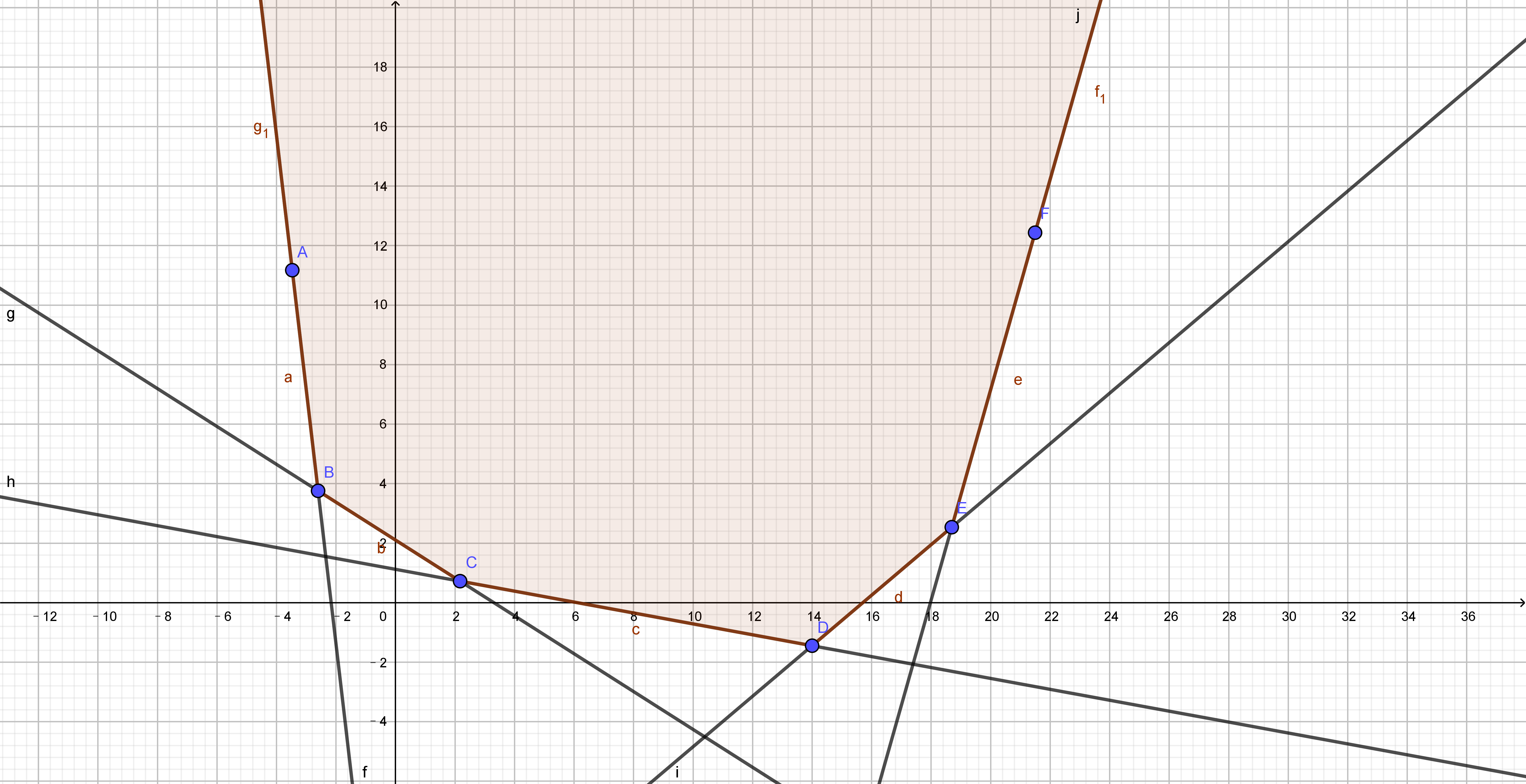
如图，图中\(x\)坐标表示选的白色边条数，\(y\)坐标表示获得的权值，那么我们就可以把\(f(x)\)在这个图上大致表示出来。我们现在并不清除\(x\)和\(y\)，所以可以二分一下和这个凸函数相切直线的斜率。设这个直线为\(y = kx + b\)，那么对于一个固定的\(x\)，截距最小的时候，就是与函数相切的时候嘛，也是答案最优的时候。

我们把这个直线转化成\(y - kx = b\)的形式。由于不清楚会选用几条边，所以可以提前给每一条白色边都减去一个\(k\)，这样不管选几条边其影响都可以被直接统计。也就是说我们现在就可以忽略选几条边的问题直接去最小化截距\(b\)了。在最小化截距的同时我们对\(y\)的值和\(x\)的值做一个记录，这样就可以做出应该取用左区间还是右区间的判定啦。

#include <bits/stdc++.h>
using namespace std;

const int N = 50000 + 5;
const int M = 100000 + 5;
#define pii pair <int, int>
#define mp(x,y) make_pair (x, y)

struct Len {
	int u, v, w, c;

	void read () {
		cin >> u >> v >> w >> c;
	}

	bool operator < (Len rhs) const {
		return w == rhs.w ? c < rhs.c : w < rhs.w;
	}
}L[M];

int n, m, k, fa[N];

int find (int x) {
	return x == fa[x] ? x : fa[x] = find (fa[x]);
}

pii Kruskal () {
	for (int i = 0; i < n; ++i) fa[i] = i;
	sort (L, L + m);
	int cnt = 0, ret = 0, wht = 0;
	for (int i = 0; i < m; ++i) {
		int fu = find (L[i].u);
		int fv = find (L[i].v);
		if (fu != fv) {
			cnt += 1;
			fa[fu] = fv;
			ret += L[i].w;
			wht += L[i].c == 0;
		}
		if (cnt == m - 1) break;
	}
	return mp (wht, ret);
} 

signed main () {
//	freopen ("data.in", "r", stdin);
	cin >> n >> m >> k;
	for (int i = 0; i < m; ++i) {
		L[i].read ();
	}
	int l = -150, r = 150, ans = 0;
	while (l < r) {
		int mid = (l + r) >> 1;
		for (int i = 0; i < m; ++i) {
			if (L[i].c == 0) { // 白色
				L[i].w -= mid;
			}
		}
		pii ret = Kruskal ();
//		cout << "l = " << l << " r = " << r << " mid = " << mid <<  " ret = (" << ret.first << ", " << ret.second << ")" << endl;
		if (ret.first >= k) {
			r = mid;
			ans = ret.second + mid * k;
		} else {
			l = mid + 1;
		}
		for (int i = 0; i < m; ++i) {
			if (L[i].c == 0) {
				L[i].w += mid;
			}
		}
	}
//	cout << l << " " << r << endl;
	cout << ans << endl;
}