「模拟赛20190327」第二题 DP+决策单调性优化

题目描述

小火车虽然很穷，但是他还是得送礼物给妹子，所以他前往了二次元寻找不需要钱的礼物。

小火车准备玩玩二次元的游戏，游戏当然是在一个二维网格中展开的，网格大小是$n\times m$的，某些格子是好的，其余的则是不好的。每次你可以选择最底层（也就是第$n$层）的某两个相邻的列，并消掉最底下的至多三个格子，并且这两列都得有格子被消掉（也就是$L$型或者反着的$L$型），消掉格子以后上面的格子会掉落下来。当然最上面的空位会用不好的格子填满。

小火车想得到所有的好格子送给妹子，请问至少得消多少次呢？

输入

第一行两个整数$n,m$，表示网格大小。

接下来$n$行每行一个长度为$m$的字符串，表示这个网格，如果为*则是好格子，为#就不是。

输出

一行一个整数表示答案。

样例

样例输入

3 2

#*

*#

##

样例输出

数据范围

对于$20\%$的数据$n,m<=5$

对于$50\%$的数据满足$n,m<=500$

对于$100\%$的数据满足$2<=n,m<=2000$

题解

诈尸啦诈尸啦。

唔……全场码量最小的题。（然而也是唯一没想出来的题）

方法很多，不过有几个很玄幻，所以我采用的是其中一种巧妙、易懂又好写的方法（没有耐心的可直接看解法$4$）。

解法$0$：暴力模拟+搜索，期望得分：$20pts$。

解法$1$：看出来这个和好格子的分布没关系，只与每一列最高的好格子有关系，然后$f[i][j]$表示前$i$列中，$i-1$列都消除完了，第$i$列恰好消除了$j$个最少需要花费多少步，暴力$DP$枚举第$i$列的$j$个是放置了$k$个反$L$型，可以轻松计算出$L$型的个数为$j-2k$，暴力$DP$，复杂度$O(n^3)$，期望得分：$50pts$。常数优秀的选手（真实案例：滚动数组+每次只枚举到这一列的最大高度+枚举反$L$型而不是枚举$L$型获得$\frac{1}{2}$的常数）可以获得$100pts$。（弥天大雾

解法$2$：考虑优化解法$1$，找最优决策点太慢了，我们随意脑补一下就知道函数值和$k$肯定是一个单谷函数的关系，因为反$L$型太多会造成自己的浪费，太少又会导致前面的浪费，感性理解可得单谷性。所以三分——等等，别忘了——这是整数，如果最后算出来相等，是无法得知该往哪边靠的。如图，你不知道你现在是红还是蓝还是绿……

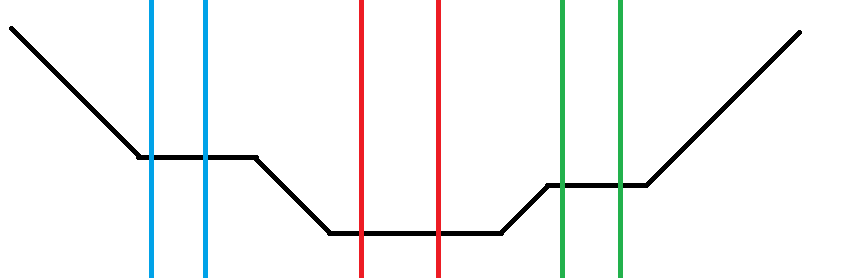
所以引入一个玄学操作：当$l、r$接近到一定程度时，就开始暴算。这个算法一看就非常玄学，你要是仔细拿捏这个度，理论上也是能过的（其实也是能过的），时间复杂度$O(n^2\log n)$，期望得分：$??pts$。

解法$3$：考虑其他优化，大佬$Freopen$提供了一个单调队列优化。容易发现，当相邻的两列比例在$[\frac{1}{2},2]$之间时，最优方案是混合使用$L$型和反$L$型，总花费$\left\lceil\frac{x+y}{3}\right\rceil$，然后枚举第$i$列与第$i-1$列一起被消去的部分长度为多少，对第$i-1$列被消去的部分进行讨论。如果是比例小于$\frac{1}{2}$或者大于$2$，那么就是全部都放的是$L$型或者反$L$型，这个很好算，否则是两个混搭起来，也就是第二维下标在当前枚举的第$i$列被消去的高度的一半和两倍之间的上一列的$dp$值，这一坨，由于要整除$3$再上取整，为了避免误差，我们按照对$3$取余的值分成三坨，这样每一坨内部的就可以用单调队列搞。当更改第$i$列的时候，就按照常规操作更新单调对列，这样复杂度是$O(n^2)$，期望得分：$100pts$。

是不是没听懂？我也没听懂。这个方法随口$bb$还是很容易说的，但是写起来可能就没有那么容易了，因此需要更简单的方法。

解法$4$：我们看到解法$2$是不是感觉很不爽，明明知道一个性质却不能用……于是我们继续思考有没有能够一起使用的性质？

首先，可以显而易见地发现，当$j$增大时，$f[i][j]$的最优决策点$k$是不会变小的，因为第$i$列需要消除更多了，如果反$L$型的变少是对消除不利的，会造成更多的浪费。那么我们考虑暴算，利用解法$2$的单谷性，一旦暴算到一个决策点使得答案更差，那么后面必然不可能更优了，直接退出。再利用决策点$k$单调性，当$j$增加的时候只需要接着上一次的$k$继续暴算就行了，因此第三维的复杂度均摊下来是$O(1)$的，代码非常好写，时间复杂度$O(n^2)$，期望得分：$100pts$。

$Code:$

#include <cstdio>

#include <cstring>

#include <iostream>

#include <algorithm>

using namespace std;

#define N 2005

#define inf 0x3f3f3f3f

void Read(int &p)

{

	p = 0;

	char c = getchar();

	for (; c < '0' || c > '9'; c = getchar());

	for (; c >= '0' && c <= '9'; c = getchar())p = p * 10 + c - '0';

}

int n, m, h[N];

int f[N][N];

char S[N][N];

int main()

{

	Read(n), Read(m);

	for (int i = 1; i <= n; i++)

	{

		scanf("%s", S[i] + 1);

		for (int j = 1; j <= m; j++)

			if (S[i][j] == '*')

				h[j] = max(h[j], n - i + 1);

	}

	memset(f, 0x3f, sizeof(f));

	f[0][0] = 0;

	//f[i][j]表示前i-1列已经被消除完，第i列被消除了j个，最少花费的步数

	for (int i = 1; i <= m; i++)

	{

		int lst = 0;

		for (int j = 0; j <= h[i]; j++)

		{

			for (int k = lst; 2 * k <= j; k++)//k表示第i列用了多少个J型，显然随着j的增大，k必定不会减少

			{

				int w = f[i - 1][max(0, h[i - 1] - k - 2 * (j - 2 * k))] + k + (j - 2 * k);

				if (w > f[i][j])break;

				f[i][j] = w;

				lst = k;

			}

		}

	}

	printf("%d\n", f[m][h[m]]);

}