Matlab随笔之分段线性函数化为线性规划
eg:
10x, 0<=x<=500
c(x)=1000+8x, 500<=x<=1000
3000+6x, 1000<=x<=1500
解法一:
可引入0-1变量,令z1=1,z2=1,z3=1分别表示0<=x<=500,500<=x<=1000,1000<=x<=1500,则
500z2<=x1<=500z1,
500z3<=x2<=500z2,
x3<=500z3,
c(x)=10x1+8x2+6x3
解法二:(更具一般性)
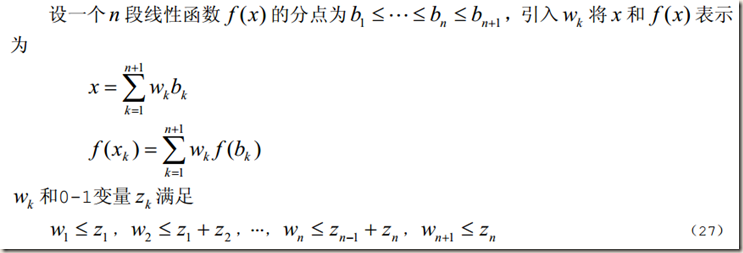
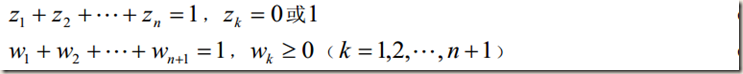
Matlab随笔之分段线性函数化为线性规划的更多相关文章
- Matlab随笔之线性规划
原文:Matlab随笔之线性规划 LP(Linear programming,线性规划)是一种优化方法,在优化问题中目标函数和约束函数均为向量变量的线性函数,LP问题可描述为:min xs.t. ...
- Matlab随笔之插值与拟合(上)
原文:Matlab随笔之插值与拟合(上) 1.拉格朗日插值 新建如下函数: function y=lagrange(x0,y0,x) %拉格朗日插值函数 %n 个节点数据以数组 x0, y0 输入(注 ...
- Matlab随笔之插值与拟合(下)
原文:Matlab随笔之插值与拟合(下) 1.二维插值之插值节点为网格节点 已知m x n个节点:(xi,yj,zij)(i=1…m,j=1…n),且xi,yi递增.求(x,y)处的插值z. Matl ...
- relu函数为分段线性函数,为什么会增加非线性元素
relu函数为分段线性函数,为什么会增加非线性元素 我们知道激活函数的作用就是为了为神经网络增加非线性因素,使其可以拟合任意的函数.那么relu在大于的时候就是线性函数,如果我们的输出值一直是在大于0 ...
- Matlab随笔之矩阵入门知识
原文:Matlab随笔之矩阵入门知识 直接输入法创建矩阵 – 矩阵的所有元素必须放在方括号“[ ]”内: – 矩阵列元素之间必须用逗号“,”或空格隔开,每行必须用“;”隔开 – 矩阵元素可以是任何不含 ...
- Matlab随笔之画图函数总结
原文:Matlab随笔之画图函数总结 MATLAB函数画图 MATLAB不但擅长於矩阵相关的数值运算,也适合用在各种科学目视表示(Scientific visualization).本节将介绍MATL ...
- Matlab随笔之指派问题的整数规划
原文:Matlab随笔之指派问题的整数规划 注:除了指派问题外,一般的整数规划问题无法直接利用Matlab函数,必须Matlab编程实现分支定界法和割平面解法. 常用Lingo等专用软件求解整数规划问 ...
- Matlab随笔之求解线性方程
原文:Matlab随笔之求解线性方程 理论知识补充: %矩阵除分为矩阵右除和矩阵左除. %矩阵右除的运算符号为“/”,设A,B为两个矩阵,则“A/B”是指方程X*B=A的解矩阵X. %矩阵A和B的列数 ...
- Matlab随笔之判别分析
原文:Matlab随笔之判别分析 从概率论角度,判别分析是根据所给样本数据,对所给的未分类数据进行分类. 如下表,已知有t个样本数据,每个数据关于n个量化特征有一个值,又已知该样本数据的分类,据此,求 ...
随机推荐
- 远离“精神乞丐”(IBM的前CEO郭士纳把员工分为四种类型)
语音丨吴伯凡 乞丐与其说是一种身份, 不如说是一种精神状态, 习惯性索取且心安理得, 习惯性寻求安慰,习惯性抱怨, 与之截然对立的, 是“操之在我”(Proactive)的精神, 乞丐型员工是公司内部 ...
- jquery插件课程1 幻灯片、城市选择、日期时间选择、拖放、方向拖动插件
jquery插件课程1 幻灯片.城市选择.日期时间选择.拖放.方向拖动插件 一.总结 一句话总结:都是jquery插件,都还比较小,参数(配置参数.数据)一般都是通过json传递. 1.插件配置数据 ...
- 【C++竞赛 A】xxx的项链
时间限制:2s 内存限制:64MB 问题描述 xxx有一个长度为n的宝石链,宝石有m种不同的颜色.xxx想截取其中连续的一段做一个项链.为了让项链更漂亮,xxx希望项链中的宝石包含所有颜色. 输入描述 ...
- QT代理Delegates使用实例(三种代理控件)
效果如下,在表格的单元格中插入控件,用Delegates方式实现 源代码如下: main.cpp文件 #include <QApplication>#include <QStanda ...
- 最新国内外可用SVN托管仓库有哪些
最新国内外可用SVN托管仓库哪些 一.总结 一句话总结:用SVNBucket和SourceForge 二.最新国内外可用SVN托管仓库推荐 这几年很多SVN托管平台都基本不维护或者直接关闭了,我翻遍了 ...
- DOM 的classList 属性
1.添加1个或多个class add(class1, class2, ...) 2.移除class remove(class1, class2, ...) 3.判断指定的类名是否存在 contains ...
- 【a703】求逆序对(树状数组的解法)
Time Limit: 10 second Memory Limit: 2 MB 问题描述 给定一个序列a1,a2...an.如果存在i小于j 并且ai大于aj,那么我们称之为逆序对,求给定序列中逆序 ...
- 热烈庆祝UE4完全免费Free---GitHub上源码的关联方法
声明:所有权利保留. 转载请说明出处:http://blog.csdn.net/cartzhang/article/details/44040317 IF YOU LOVE SOMETHING, SE ...
- [Ramda] Refactor a Promise Chain to Function Composition using Ramda
Promise chains can be a powerful way to handle a series of transformations to the results of an asyn ...
- iOS 下载功能:断点下载(暂停和开始)(NSURLConnectionDataDelegate方法)
1,model文件代码 文件名称:HMFileDownloader.h #import <Foundation/Foundation.h> @interface HMFileDownloa ...
