Binary Indexed Tree
我借鉴了这个视频中的讲解的填坑法,我认为非常易于理解。有翻墙能力和基本英语听力能力请直接去看视频,并不需要继续阅读。
naive 算法
考虑一个这样的场景: 给定一个int数组, 我们想知道它的连续子序列的累加和。比如这个数组长度为N, 求数组中下标0~N-1, 2~3, 0~N/2的和。 如果直接计算,易知在平均情况下,我们给出一个N长度数组的子序列累加和都需要~N的数组访问次数和相加操作。
如果用最少的计算时间给出结果? 我们容易想到设一个记录累加和的数组(不考虑可能的溢出情况): 比如数组[1, 2, 3, 4, 5], 我们为它生成一个累加和数组[1, 3, 6, 10, 15]。生成这个数组需要一次遍历,即N次访问操作。而我们给出累加和结果的时候,可以1常数次访问累加和数组直接给出结果。
但是,当我们需要更新数组中的元素的时候呢? 直接在数组上操作需要~1次访问。 如果我们使用了累加数组,则需要对累加数组也进行更新,平均每次更新需要对累加和数组进行~N次访问。 所以我们可以给出以下的表格:
update 更新操作
sum 获取子序列累加值操作
construct 构建初始辅助数据结构
| 操作 | construct | sum | update |
|---|---|---|---|
| 暴力相加 | 0 | ~N | ~1 |
| 累加数组 | ~N | ~1 | ~N |
在频繁操作的情况下, 尤其是sum和update的操作次数接近的时候, 暴力相加和使用了累加数组的效率是相近的。 考虑操作M次, M接近于N的情况下, 这两种处理方式的时间复杂度都是 ~M * N 是一个平方级的算法。 在很多场景中,平方级的算法都被认为是不可接受的。
这种场景中,使用 Binary Indexed Tree 和 Segment Tree 都能对效率起到数量级的提升作用。 尤其是 Binary Indexed Tree, 易于理解, 实现起来也短小精美。
通过填坑法理解Binary Idexed Tree
首先,Binary Indexed Tree的实现上, 并不是我们从字面意思上想到的编程实现了一个树形结构。 叫它是 Binary Indexed Tree 是因为对它进行操作的时候体现了逻辑层次上的层次关系。
给定以下场景, 一个长度为N的int数组,想对它进行求子序列和操作。 我们基于这个数组构建的Binary Indexed Tree 也是一个存储在长度为N的int数组(此处不考虑溢出)。而如何构建这个长度为N的序列即Binary Indexed Tree, 是理解Binary Indexed Tree的关键。
我们给出一个数组:
数组:[ 0, 2, 0, 1, 1, 1, 0, 4, 4, 0, 1, 0, 1, 2, 3, 0 ]
下标: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
为了在构建Binary Indexed Tree的时候方便(将简化一些位操作代码), 我们把它由从0开始的初始下标改为从1开始的初始下标:
数组:[ 0, 2, 0, 1, 1, 1, 0, 4, 4, 0, 1, 0, 1, 2, 3, 0 ]
下标: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Binary Indexed Tree的思想是,每一个整数都可以由几个二进制指数的相加和唯一表示:
例如: 11 = 2^3 + 2^1 + 2^0
这是因为每个数的二进制表示都是唯一的: 11 的二进制表示 1011 即对应了上面的式子.
Binary Indexed Tree 要处理的这个数,就是下标。 按照Binary Indexed Tree的逻辑, 我们要计算下标1~11的元素的累加和,应该分别计算头2^3个元素的的累加和(即1~8的累加和), 然后加上接下来的2^1个元素的累加和(即9~10的累加和), 最后加上2^0个元素的累加和(11~11的累加和)。 下面表示更清晰:
数字 11 = 2^3 + 2^1 + 2^0
数字 11 = 8 + 2 + 1
序列 1~11 = 1~8 + 9~10 + 11
序列和 SUM(11)= BIT[8] + BIT[10] + BIT[11]
构建Binary Indexed Tree之后,设构建的数组名为BIT, 下标从1开始,长度为N。
接下来要谈的就是如何构建Binary Indexed Tree. Fenwick的论文中和网上很多教程中给出了这样的图片。

我个人认为对于初学者并不好理解。 而这个视频中的讲解的填坑法,我认为非常易于理解。有翻墙能力和基本英语听力能力请直接去看视频,并不需要继续阅读。
如果你还在看。唔,还是这个数组, 我们来构建它的BIT(Binary Indexed Tree)

第一层,我们面对的是1~16这个区间,我们需要填充1~16这个区间中所有下标为从1开始计数的2的指数次 (1, 2, 4, 8, 16)的BIT数组, 填充的值是从1开始到对应下标的的累加值:
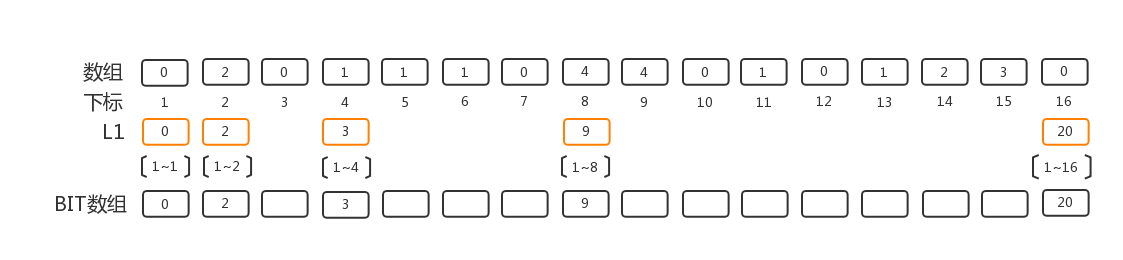
第二层,我们要填充的是3~3, 5~7, 9~15三个区间, 同样,我们填充每个区间从开始下标开始计数为2的指数次的BIT的元素。 以9~15区间为例,从9开始, 9计数为1即2^0,10计数为2即2^1的元素,12计数为4即2^2, 所以下标为9, 10, 12的元素就是我们这层要填充的元素,分别对应于区间9~9, 9~10, 9~12的累加值. 另外两个区间方式类似。
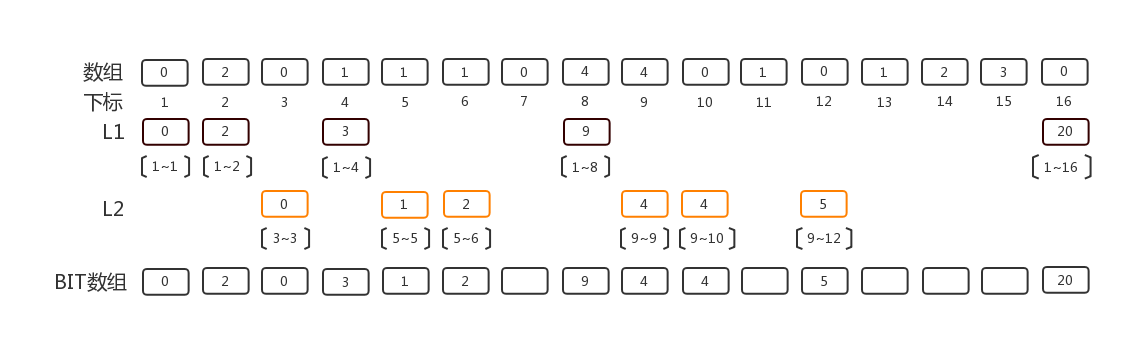
第三层,我们要填充的是, 7~7, 11~11, 13~15区间,用同样的方法来进行填充
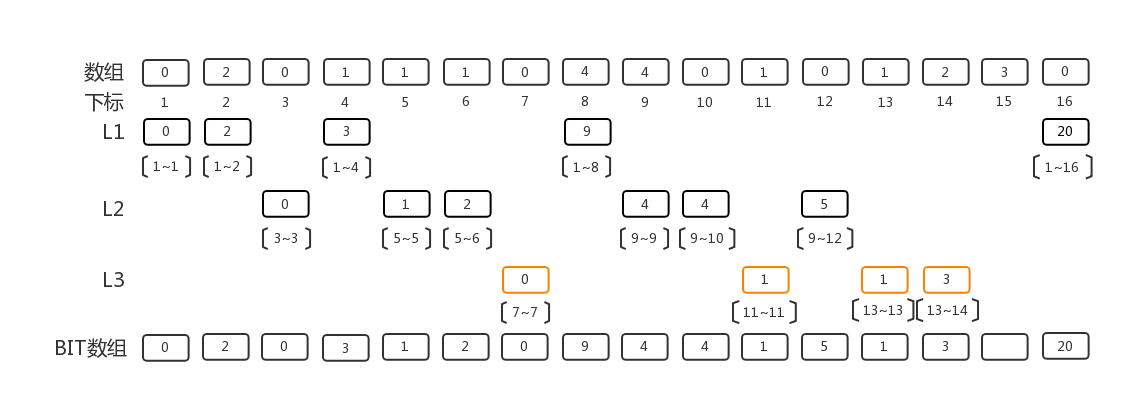
第四层, 我们只有15~15区间需要填充了, 至此一个BIT数组填充完毕
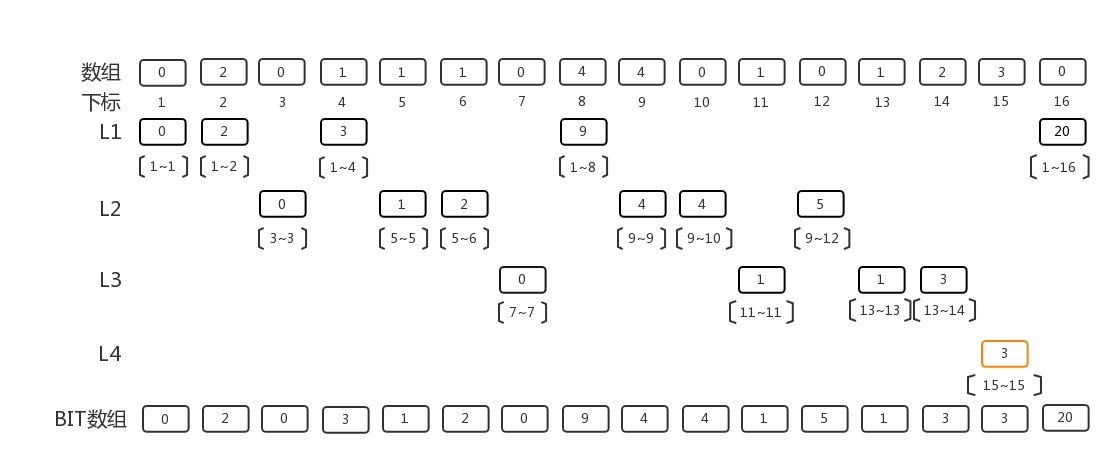
求1~K区间的累加和的sum操作
上面的过程是通过填充BIT数组,展示了BIT数组各个下标对应的值是怎么来的。那么我们如何利用这个数组来进行求和呢?
我们以求区间1~15的累加和为例, 展示这种逐层累加来进行求和的方法。 从BIT[15]开始,距离BIT[15]最近的上层是BIT[14], 距离BIT[14]最近的上层是BIT[12], 距离BIT[12]最近的上层是BIT[8], 至此BIT[8]已经没有上层了,我们停止累加。 所以,区间1~15的累加和就是 BIT[15] + BIT[14] + BIT[12] + BIT[8] = 20

但是,这种找上层最近结点的功能怎么用代码来实现呢?
我们只需要稍加观察这些BIT数组下标的二进制表示,就会发现从15 -> 14 -> 12 -> 8的过程, 实际上就是依次把每个数字的二进制表示的最后(从左往右看)一个1反转为0的过程。 也正对应了15 = 2^3 + 2^2 + 2^1 + 2^0, 依次去掉最小的2的指数项的过程。这就是Binary Indexed Tree求累加和的规律。

所以,利用一个BIT数组求1~K区间的累加和,需要从BIT[K]项开始, 依次翻转K的二进制表示的最后一个1来获取下一项, 直到归零。 然后把所有获取到的项加起来, 即是1~K区间上的累加和。
具体来讲,如何翻转最后一个1? 这里我们要讲到一个trick:
还是以下标15为例, 8bit字长时(32bit, 64bit情况相似) 15的补码表示是00001111, -15的补码表示是11110001,我们发现是00001111和11110001按位相与就能提取出00000001, 即是二进制表示的最后一位1。 然后我们用15直接减去这个提取出的数字,实际上就是进行了翻转。 即 15 - 15&(-15) ==> 00001111 - (00001111 & 11110001) ==> 00001110 = 14 就得到了下一项。 这是一个非常简练的式子, BIT[K]的下一项就是BIT[K - (K & -K)]。 大家可以自己对照图片实验。 由此, 我们可以得到我们的第一段程序:
int sum(int k){
int sum = 0;
while (k > 0){
sum += BIT[k];
k -= (k & -k);
}
return sum;
}
如何衡量利用BIT计算1~K的累加和的效率?
从图上来说,我们可以看到与形成的BIT的层次有关。 对一个BIT数组进行sum操作, 对BIT数组访问次数最多的就是层次最深的结点。 从二进制表示的角度来说,至多不超过其下标的二进制表示中最多的1的个数。 这正是一个log的关系,对于长度为N的BIT数组,一次sum操作访问数组次数的上界就是 logN + 1
对第k项进行更新的update操作
log级别的sum操作确实比线性的暴力操作有不小提升,但是相比于使用累加数组的常数次访问还是慢。 Binary Indexed Tree的优越性体现在对BIT数组进行update操作的数组访问次数也可以缩小到log级别。
考虑对原数组下标为6的元素进行+2操作,会如何影响BIT数组?
首先我们从图上看到BIT[6]表示了5~6区间元素的累加和, 所以BIT[6]需要+2, 然后我们再在BIT数组中找更新元素6影响到的区间, 发现BIT[8]表示了1~8区间的累加和包含第六个元素, BIT[8]也需要+2, 然后BIT[16]表示了1~16区间的累加和, 也需要+2。 BIT数组中再找不到包含第六个元素的区间, 我们对BIT数组的更新就完成了。 如下图所示:
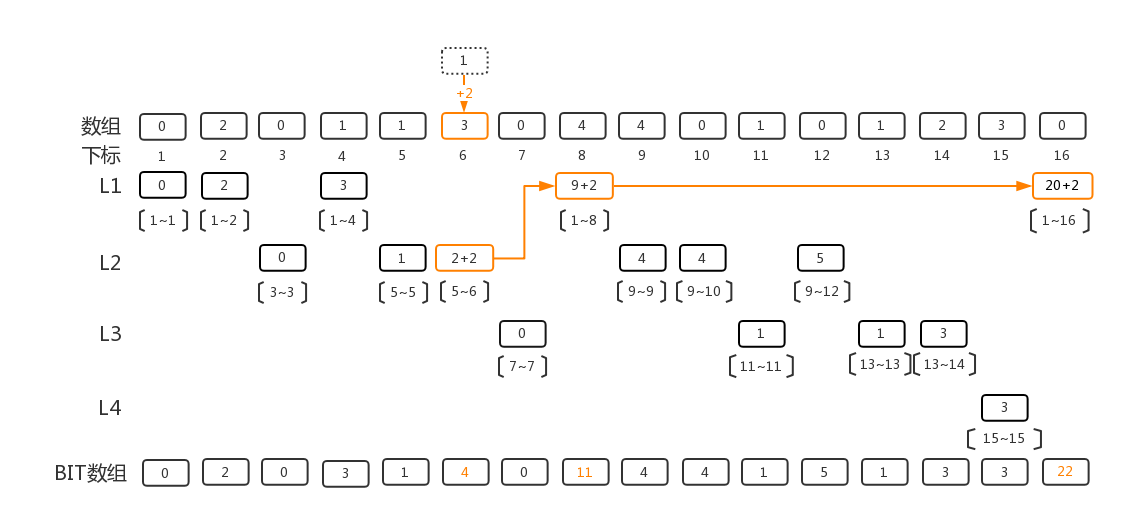
同样,我们也想到,如何编程实现找到需要更新的区间呢? update操作和sum操作是相反的方向,实际上并不是同一个树形结构。这里我们再次把下标展开为二进制形式:
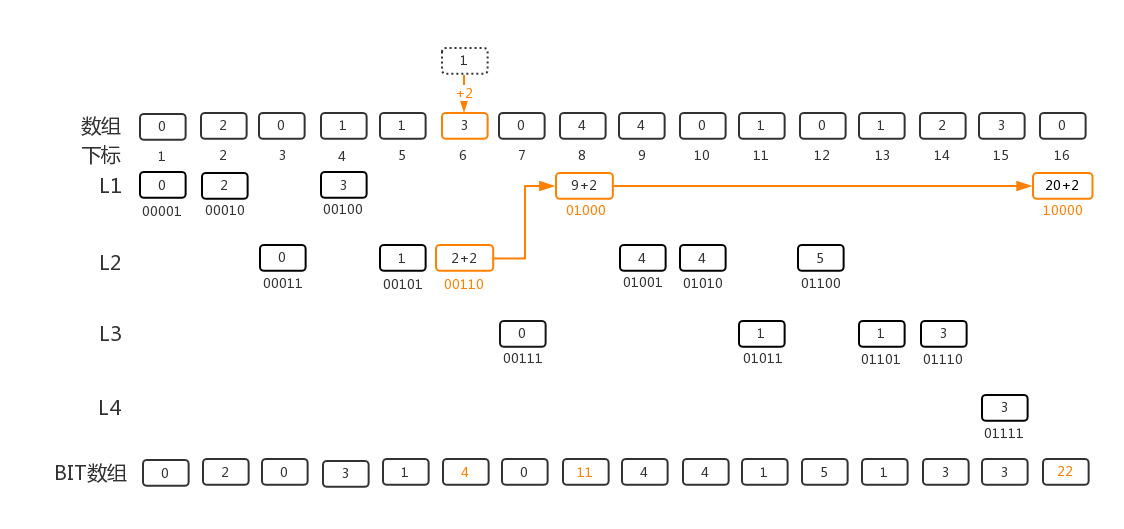
从被update的下标K开始, 所有被影响到的BIT数组元素的下标可以由K逐个推得。 这里的规律是, 以6的二进制表示00110开始, 可以找到的下一个下标为 00110 + 00010 = 01000 即为8, 从8的二进制表示01000开始, 01000 + 01000 = 10000 即为16。 这次,我们从K开始, 把K加上其二进制表示的最后一位1形成的数字,即推导出下一项的下标。 而我们从sum函数中已经知道的trick是 K & -K 就可以提取出最后一位为1的数。 所以, BIT[K]的下一项就是BIT[K + (K & -K)]。 update的代码实现为:
// N 为BIT数组长度
// val 为更新值
int update(int k, int val){
while (k <= N){
BIT[k] += val;
k += (k & -k);
}
}
由此,我们也可以得到update操作的时间复杂度。 从二进制表示的角度来看,因为每寻找一次下一项都是找最后一位为1的位数更高的, 所以对于长度为N的BIT数组, 至多需要翻转logN次就可以完成一次更新。
至于Binary Indexed Tree的建立
到现在,可能有人有疑问, 我们只讲了sum操作和update操作, 并没有讲如何构建一个Binary Indexed Tree(construct操作)啊。 并且,从图片上看的填坑法虽然容易理解,但是程序写起来也是比较麻烦的吧。
其实换个思路, 如果我们把初始数组设为全0的数组, 然后依次把数组中的元素都进行一次update操作,不就完成了对BIT数组的构建吗?
Binary Indexed Tree的效率和拓展
每次update平均消耗logN次数组访问操作, 构建一个长度为N的数组的BIT数组的时间复杂度是NlogN级别的。我们可以更新我们的表格了:
| 操作 | construct | sum | update |
|---|---|---|---|
| 暴力相加 | 0 | ~N | ~1 |
| 累加数组 | ~N | ~1 | ~N |
| Binary Indexed Tree | ~NlogN | ~logN | ~logN |
还是在频繁操作的情况下, sum和update的操作次数接近的时候, 暴力相加和使用了累加数组的效率是相近的。 考虑操作M次, M接近于N的情况下, 这两种处理方式的时间复杂度都是 ~M * N 是一个平方级的算法。Binary Indexed Tree可以达到 ~ M * log N 级别的时间复杂度。 这是一个比较大的提升。尤其是,其代码实现短小精美, 让人印象深刻。
同时,注意观察的话, 以1为初始下标, 我们发现BIT数组中的奇数下标的元素都是直接存了原数组元素的值, 而偶数下标的原数组的值也可以通过BIT数组在比较小的消耗的情况下得到(可以看论文和其他介绍了解)。 所以, Binary Indexed Tree在一定效率容忍情境下,可以直接用BIT数组,而不需要保留原数组,这将是一个空间上的原地算法。
并且,BIT数组还可以被拓展到多维的应用。
就我个人的感受, Binary Indexed Tree和红黑树都体现了一种结构初看有些复杂,但是代码实现起来却非常精炼的算法的美感。 为这样的"聪明"点赞。
并在文章结尾吐槽一下博客园的Markdown渲染还真是...难看。
Binary Indexed Tree的更多相关文章
- Leetcode: Range Sum Query 2D - Mutable && Summary: Binary Indexed Tree
Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper lef ...
- SRM 627 D1L2GraphInversionsDFS查找指定长度的所有路径 Binary indexed tree (BIT)
题目:http://community.topcoder.com/stat?c=problem_statement&pm=13275&rd=16008 由于图中边数不多,选择DFS遍历 ...
- 树状数组(Binary Indexed Tree,BIT)
树状数组(Binary Indexed Tree) 前面几篇文章我们分享的都是关于区间求和问题的几种解决方案,同时也介绍了线段树这样的数据结构,我们从中可以体会到合理解决方案带来的便利,对于大部分区间 ...
- Binary Indexed Tree (Fenwick Tree)
Binary Indexed Tree 主要是为了存储数组前缀或或后缀和,以便计算任意一段的和.其优势在于可以常数时间处理更新(如果不需要更新直接用一个数组存储所有前缀/后缀和即可).空间复杂度O(n ...
- Hdu5921 Binary Indexed Tree
Hdu5921 Binary Indexed Tree 思路 计数问题,题目重点在于二进制下1的次数的统计,很多题解用了数位DP来辅助计算,定义g(i)表示i的二进制中1的个数, $ans = \su ...
- Binary Indexed Tree 总结
特点 1. 针对 数组连续子序列累加和 问题(需要进行频繁的 update.sum 操作): 2. 并非是树型结构,只是逻辑上层次分明: 3. 可以通过 填坑法 来理解: 4. 中心思想:每一个整数都 ...
- 树状数组(Binary Indexed Tree)
树状数组(Binary Indexed Tree,BIT) 是能够完成下述操作的数据结构. 给一个初始值全为 0 的数列 a1, a2, ..., an (1)给定 i,计算 a1+a2+...+ai ...
- Fenwick Tree / Binary Indexed Tree
Motivation: Given a 1D array of n elements. [2, 5, -1, 3, 6] range sum query: what's the sum from 2n ...
- Binary Indexed Tree 2D 分类: ACM TYPE 2014-09-01 08:40 95人阅读 评论(0) 收藏
#include <cstdio> #include <cstdlib> #include <climits> #include <cstring> # ...
随机推荐
- 英语发音规则---S字母
英语发音规则---S字母 一.总结 一句话总结: 1.S 在音节开头或清辅音前 /s/? sit /sɪt/ vt.& vi.坐 seat /si:t/ n.席位 sell /sel/ vt. ...
- php面向对象之__isset和__unset
php面向对象之__isset和__unset 一.简介 __isset和__unset都是对不可访问属性的操作,前者是检验的时候自动调用,后者是销毁的时候自动调用. 比如说在类外访问private的 ...
- 转:centos下升级git版本的操作记录
https://www.cnblogs.com/kevingrace/p/8252517.html 在使用git pull.git push.git clone的时候,或者在使用jenkins发版的时 ...
- python一行代码实现9x9乘法表
for i in range(1,10): for j in range(1,i+1): print('%s * %s = %s ' %(i,j,i*j),end="") prin ...
- POJ 3185 DFS
好像可以用高斯消元??? 但是用搜索写 这题就很水了... // by SiriusRen #include <bitset> #include <cstdio> using ...
- Linux中安装redis的phpredis扩展
下载phpredis扩展 http://pecl.php.net/package/redis wget http://pecl.php.net/get/redis-4.0.2.tgz 需要环境配置文件 ...
- Usaco 滑雪比赛 Bobsledding, 2009 Dec(dp)
Description 滑雪比赛bobsled 贝西参加了一场高山急速滑雪比赛,滑道总长度为 L.出发时,她的初速度为 1,贝西可以加速 或减速,每过 1 米,她能将速度增加 1.减少 1 或保持不变 ...
- 『转』How to Think About Your Career
开始工作的伊始,逐渐转载及阅读Medium上知名华裔设计师Julie Zhuo的文章,这是她在medium上的介绍:Product design VP @ Facebook. Lover of foo ...
- oc与swift比较
swift试是用语言层面的雕虫小技和oc的机制大道进行pk. 从整体上来说,oc是一个更加优秀的语言.
- unity 模型 材质 贴图 关系;着色器属性
模型包含 材质(Material),包括 [核心]着色器(Shader) 贴图和其他参数,贴图也算是一种参数 其他,如网格渲染器(Mesh Renderer).动画.坐标 一个材质可以看做为一个Sha ...
