n个元素进栈，共有多少种出栈顺序？

1.基于栈的问题分析

我们把n个元素的出栈个数的记为f(n), 那么对于1,2,3, 我们很容易得出：

                                  f(1) = 1     //即 1

                                     f(2) = 2     //即 12、21

                                     f(3) = 5     //即 123、132、213、321、231

然后我们来考虑f(4), 我们给4个元素编号为a,b,c,d, 那么考虑：元素a只可能出现在1号位置，2号位置，3号位置和4号位置(很容易理解，一共就4个位置，比如abcd,元素a就在1号位置)。

分析：

1) 如果元素a在1号位置，那么只可能a进栈，马上出栈，此时还剩元素b、c、d等待操作，就是子问题f(3)；

2) 如果元素a在2号位置，那么一定有一个元素比a先出栈，即有f(1)种可能顺序（只能是b），还剩c、d，即f(2)，     根据乘法原理，一共的顺序个数为f(1) * f(2)；

3) 如果元素a在3号位置，那么一定有两个元素比1先出栈，即有f(2)种可能顺序（只能是b、c），还剩d，即f(1)，

    根据乘法原理，一共的顺序个数为f(2) * f(1)；

4) 如果元素a在4号位置，那么一定是a先进栈，最后出栈，那么元素b、c、d的出栈顺序即是此小问题的解，即f(3)；

结合所有情况，即f(4) = f(3) + f(2) * f(1) + f(1) * f(2) + f(3);

为了规整化，我们定义f(0) = 1；于是f(4)可以重新写为：

f(4) = f(0)*f(3) + f(1)*f(2) + f(2) * f(1) + f(3)*f(0)

然后我们推广到n，推广思路和n=4时完全一样，于是我们可以得到：

f(n) = f(0)*f(n-1) + f(1)*f(n-2) + ... + f(n-1)*f(0)

即

 

---

但这只是一个递推公式（若编程实现，需要维护一个一维数组，时间复杂度为O(n^2)）。怎么把它转化为通项公式呢，复杂度仅为O(1)?

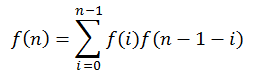
2. 相关的求解方法

（1）非常规数值分析

对于每一个数来说，必须进栈一次、出栈一次。我们把进栈设为状态‘1’，出栈设为状态‘0’。n个数的所有状态对应n个1和n个0组成的2n位二进制数。由于等待入栈的操作数按照1‥n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b)，因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数，1的累计数不小于0的累计数的方案种数。

在2n位二进制数中填入n个1的方案数为c(2n,n),不填1的其余n位自动填0。从中减去不符合要求（由左而右扫描，0的累计数大于1的累计数）的方案数即为所求。

不符合要求的数的特征是由左而右扫描时，必然在某一奇数位2m+1位上首先出现m+1个0的累计数和m个1的累计数，此后的2(n-m)-1位上有n-m个 1和n-m-1个0。如若把后面这2(n-m)-1位上的0和1互换，使之成为n-m个0和n-m-1个1，结果得1个由n+1个0和n-1个1组成的2n位数，即一个不合要求的数对应于一个由n+1个0和n-1个1组成的排列。

反过来，任何一个由n+1个0和n-1个1组成的2n位二进制数，由于0的个数多2个，2n为偶数，故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换，使之成为由n个0和n个1组成的2n位数，即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数。

因而不合要求的2n位数与n+1个0，n－1个1组成的排列一一对应。

显然，不符合要求的方案数为c(2n,n+1)。

      由此得出输出序列的总数目=c(2n,n)-c(2n,n+1)=c(2n,n)/(n+1)。其中，n为节点的个数。

（2）从图像上分析

事实上，可以认为问题是，任意两种操作，要求每种操作的总次数一样，且进行第k次操作2前必须先进行至少k次操作1。我们假设一个人在原点，操作1是此人沿右上角45°走一个单位（一个单位设为根号2，这样他第一次进行操作1就刚好走到（1,1）点），操作2是此人沿右下角45°走一个单位。第k次操作2前必须先进行至少k次操作1，就是说明所走出来的折线不能跨越x轴走到y=-1这条线上！在进行n次操作1和n此操作2后，此人必将到到达（2n，0）！若无跨越x轴的限制，折线的种数将为C（2n，n），即在2n次操作中选出n次作为操作1的方法数。

现在只要减去跨越了x轴的情况数。对于任意跨越x轴的情况，必有将与y=-1相交。找出第一个与y=-1相交的点k，将k点以右的折线根据y=-1对称（即操作1与操作2互换了）。可以发现终点最终都会从（2n，0）对称到（2n，-2）。由于对称总是能进行的，且是可逆的。我们可以得出所有跨越了x轴的折线总数是与从（0,0）到（2n,-2）的折线总数。而后者的操作2比操作1要多0-（-2）=2次。即操作1为n-1,操作2为n+1。总数为C（2n，n-1）。（此处类似于上面的数值角度分析）

（3）卡特兰数介绍

令h(0)=1,h(1)=1，catalan数满足递推式^[1]：

h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)

例如：h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2

h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5

 

递推关系的解为：

h(n)=C(2n,n)/(n+1) (n=0,1,2,...)

递推关系的另类解为：

h(n)=c(2n,n)-c(2n,n+1)(n=0,1,2,...)

3.类似的问题

（1）买票找零

有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)

（2）一个有n个1和n个-1组成的字串，且前k个数的和均不小于0，那这种字串的总数为多少？

（3）饭后，姐姐洗碗，妹妹把姐姐洗过的碗一个一个地放进碗橱摞成一摞。一共有n个不同的碗，洗前也是摞成一摞的，也许因为小妹贪玩而使碗拿进碗橱不及时，姐姐则把洗过的碗摞在旁边，问：小妹摞起的碗有多少种可能的方式？

最终结果：C(2n,n)-C(2n,n+1)