二维动态规划——Interleaving String

97. Interleaving String

Given s1, s2, s3, find whether s3 is formed by the interleaving of s1 and s2.

For example, Given: s1 = "aabcc", s2 = "dbbca",

When s3 = "aadbbcbcac", return true.

When s3 = "aadbbbaccc", return false.

类似于最长公共子序列，从字符尾部开始处理，解题思路很容易找到，递归来做很简单，但是会超时。

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        if(s3.length() != s1.length() + s2.length())
            return false;
        return isInterleave(s1, s2, s3, s1.length() - 1, s2.length() - 1, s3.length() - 1);
    }
private:
    bool isInterleave(string &s1, string &s2, string &s3, int i1, int i2, int i3) {
        if(i3 < 0) //i3最先到-1
            return i1 < 0 && i2 < 0;
        return (s1[i1] == s3[i3] && isInterleave(s1, s2, s3, i1 - 1, i2, i3 - 1)) ||
               (s2[i2] == s3[i3] && isInterleave(s1, s2, s3, i1, i2 - 1, i3 - 1));
    }
};

其实递归中用不上i1、i2、i3这3个状态标志，因为任意两个标志可以表示第三个标志，状态的设计对解题有时很关键。

可以看出该问题满足最优子结构特征和重叠子问题特征，那么试着使用动态规划来改进时间复杂度。

设dp[i][j]表示s[0..i]与s2[0..j]匹配s3[0..(i + j)]，则状态转移方程为：

dp[i][j] = (dp[i - 1][j] && s1[i - 1] == s3[i + j - 1]) || (dp[i][j - 1] && s2[j - 1] == s3[i + j - 1])，子问题数目为O(n^{2)，每个子问题需要用到O(n}0)个子问题的结果，跟最长公共子序列问题一样，同属于2D/0D问题。

这是一个二维动态规划问题，边界条件即当i = 0或j = 0时，当达到边界条件时就退化为一维动态规划问题。

当i = 0时，状态转移方程退化为dp[0][j] = (dp[0][j - 1] && s2[j - 1] == s3[j - 1])，

当j = 0时，状态转移方程退化为dp[i][0] = (dp[i - 1][0] && s1[i - 1] == s3[i - 1])。

可以提前把边界情况计算好，也可以边填表边计算，一般很难说哪种好一些，不过在该情况下实测边填表边计算要好一些。

状态转移图如下，横轴表示s1，纵轴表示s2，其中每一个状态必须访问图中左下角的状态，那么可以先解决左下角的子问题，再计算原问题，这样避免重复计算，最终返回dp[s1.length()][s2.length()]即可。该算法时间复杂度为O(N^{2)，空间复杂度为O(N}2)。

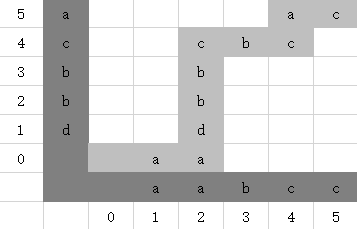
提前把边界情况计算好，代码如下。

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        if(s3.length() != s1.length() + s2.length())
            return false;
        vector<vector<bool>> dp(s1.length() + 1, vector<bool>(s2.length() + 1, true));
        for(size_t i = 1; i <= s1.length(); ++i)
            dp[i][0] = dp[i - 1][0] && s1[i - 1] == s3[i - 1];
        for(size_t j = 1; j <= s2.length(); ++j)
            dp[0][j] = dp[0][j - 1] && s2[j - 1] == s3[j - 1];
        for(size_t i = 1; i <= s1.length(); ++i) {
            for(size_t j = 1; j <= s2.length(); ++j) {
                dp[i][j] = (dp[i - 1][j] && s1[i - 1] == s3[i + j - 1]) ||
                           (dp[i][j - 1] && s2[j - 1] == s3[i + j - 1]);
            }
        }
        return dp[s1.length()][s2.length()];
    }
};

//使用滚动数组优化
class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        if(s1.length() + s2.length() != s3.length())
            return false;
        if(s1.length() < s2.length())
            return isInterleave(s2, s1, s3);
        vector<bool> dp(s2.length() + 1, true);
        for(size_t i = 1; i <= s2.length(); ++i)
            dp[i] = s2[i - 1] == s3[i - 1] && dp[i - 1];
        for(size_t i = 1; i <= s1.length(); ++i) {
            dp[0] = s1[i - 1] == s3[i - 1] && dp[0];
            for(size_t j = 1; j <= s2.length(); ++j)
                dp[j] = (dp[j] && s1[i - 1] == s3[i + j - 1]) ||
                        (dp[j - 1] && s2[j - 1] == s3[i + j - 1]);
        }
        return dp[s2.length()];
    }
};

边填表边计算，代码如下。

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        if(s3.length() != s1.length() + s2.length())
            return false;
        bool dp[s1.length() + 1][s2.length() + 1];
        for(size_t i = 0; i <= s1.length(); i++) {
            for(size_t j = 0; j <= s2.length(); j++) {
                if(i == 0 && j == 0)
                    dp[i][j] = true;
                else if(i == 0)
                    dp[i][j] = (dp[i][j - 1] && s2[j - 1] == s3[i + j - 1]);
                else if(j == 0)
                    dp[i][j] = (dp[i - 1][j] && s1[i - 1] == s3[i + j - 1]);
                else
                    dp[i][j] = (dp[i - 1][j] && s1[i - 1] == s3[i + j - 1]) ||
                               (dp[i][j - 1] && s2[j - 1] == s3[i + j - 1]);
            }
        }
        return dp[s1.length()][s2.length()];
    }
};