[C++进阶] 数据结构与算法

1 出栈&入栈问题

一个栈的入栈序列为ABCDE，则不可能的出栈序列为?（不定项选择题）
A：ECDBA  B：DCEAB   C：DECBA   D：ABCDE   E：EDCBA

正确答案是：AB

解析如下：

首先，入栈与出栈是交错进行的，也就是A入栈后可能立马就出栈了。也可能A、B都入栈后，再让B出栈。

• 选项A：A入，B入，C入，D入，E入。想要出栈顺序为ECD，那么E要先出，也就是E必须是最后一个入栈，第一个出栈的，那么CD先后出栈的情况是不存在的。即选项A为false；
• 选项B：A入，B入，C入，D入，D出，C出，E入，E出，B出，A出，也就是说，按照DCE的顺序，最后出栈的应该是BA才对。即选项B为false；
• 选项C：A入，B入，C入，D入，D出，E入，E出，C出，B出，A出，即选项C为true；
• 选项D：A入，A出，B入，B出，C入，C出，D入，D出，E入，E出，即选项D为true；
• 选项E：A入，B入，C入，D入，E入，E出，D出，C出，B出，A出，即选项E为true。

故，选项A与B是不可能出现的。

2 计算完全二叉树的叶子数目

一个完全二叉树有770个节点，那么其叶子的个数为 :_____?

解析：对于一个完全二叉树，如果总结点数为偶数，则度为 1 的结点数为1，如果总结点数为奇数且大于 1，则度为 1 的结点数为 0；而总结点数 770 为偶数，所以度为 1 的结点数 n1 = 1；度为 0 的结点数与度为 2 的结点数：n0 = n2 + 1；所以总结点数：n0+n1+n2 = 2n0 - 1 + 1 = 770，所以n0 = 385，即叶子结点的个数。

3 怎么判断链表中是否有环？

有多种思路可以解决，这里我们只介绍快慢指针法。

首先我们要理解什么是快慢指针。快指针 fast 每次移动 2 个节点，慢指针 slow 每次移动 1 个节点，如果快指针能够追上慢指针，那就说明其中有一个环，否则不存在环。

// 快慢指针法
int testLinkRing(LinkList *head)
{
    LinkList *slow = head, *fast = head;
    while (slow->next && fast->next)
    {
        slow = slow->next;
        if (NULL == (fast = fast->next->next))
            return 0;   //无环
        if (slow == fast)
            return 1;   //有环
    }

    return 0;
}

4 返回链表倒数第N个节点

5 删除链表中的重复项

采用三个指针来进行遍历，同时删除重复的节点，因为是有序的链表，我们就可以确定，重复的元素肯定是在一块链接，所以我们就可以，用三指针，我们这里就叫 pre、cur、next 分别代表的是前中后三个指针，我们在考虑的情况中，如果头节点开始就重复，我们就处理很起来多了一种情况就需要额外处理，所以我们添加一个头节点，变成带头节点，保证了头节点开始不会重复，那么我们就可以让 pre 指向带头的节点，cur 指向 pre 的next，nex 指向 cur 的next。

接下来我们就可以看 cur 是否和 nex 相等，相等就让 next 继续向下走，不相等然后再处理删除，cur 开始到 next 中间节点都是要删除的（包含 cur 指向，不包含 next 指向）删除，就用到了 pre，删除完成让 pre 指向 cur 就可以了。

如果 cur 值与 next 值不相等，那么就可以三个指针各自往前移动一个。

ListNode* deleteDuplication(ListNode* pHead)
{
	// 先判断空
	if (pHead == NULL)
	{
		return NULL;
	}
	// 判断是否只有一个节点
	if (pHead->next == NULL)
	{
		return pHead;
	}
	// 我们采用带头链表，自己添加一个头
	ListNode* pre = new ListNode();
	pre->next = pHead; // 把头节点链接在链表上
	ListNode* pre_head = pre; // 用来保存头节点，用于返回删除后的链表
	ListNode* cur = pHead; //中指针
	ListNode* nex = pHead->next; // 后面指针
	while (nex != NULL) // 结束条件
		while (nex != NULL && cur->val == nex->val)
		{
			nex = nex->next;
		}
		// 如果没有重复的那么cur的next一定等于nex
		if (cur->next != nex) // 如果相等说明没有相同的节点
		{
			while (cur != nex) // 删除动作
			{
				pre->next = cur->next;
				delete cur;
				cur = pre->next;
			}
			if (nex != NULL) // 这里一定要要注意，要防止走到NULL发生段错误
			nex = nex->next;
		}
		else
		{
			// 处理没有重复的情况
			pre = cur;
			nex = nex->next;
			cur = cur->next;
		}
	}
	ListNode* head = pre_head->next; // 释放空间，防止内存泄漏
	delete pre_head;
	return head;
}

6 根据要求写出函数（链表相关）。

有两个双向循环链表 A，B，知道其头指针为：pHeadA，pHeadB，请写一函数将两链表中 data 值相同的结点删除。

typedef struct node
{
    int data;
    struct node *prior,*next;
}LinkNode;

void deleteSame(LinkNode *pHeadA, LinkNode *pHeadB)
{
    // 判断链表是否存在
    if(!pHeadA || pHeadB)
    {
        printf("链表不存在!\n");
        return;
    }

    // 双层遍历链表
    int breakFalg = 0; // 用于跳出第一层循环
    LinkNode *curA = pHeadA->next;
    while(curA != pHeadA)
    {
        LinkNode *curB = pHeadB->next;
        while(curB != pHeadB)
        {
            if(curB->data == curA->data)
            {
                // 删除A节点
                if(curA->next != NULL)
                    curA->next->prior = curA->prior;
                curA->prior->next = curA->next;
                free(curA);
                curA = NULL;

                // 删除B节点
                if(curB->next != NULL)
                    curB->next->prior = curB->prior;
                curB->prior->next = curB->next;
                free(curB);
                curB = NULL;

                breakFalg = 1;
                break;
            }

            curB = curB->next;
        }

        if(breakFalg == 1)
            break;

        curA = curA->next;
    }
}

7 二叉树的3种非递归遍历方法

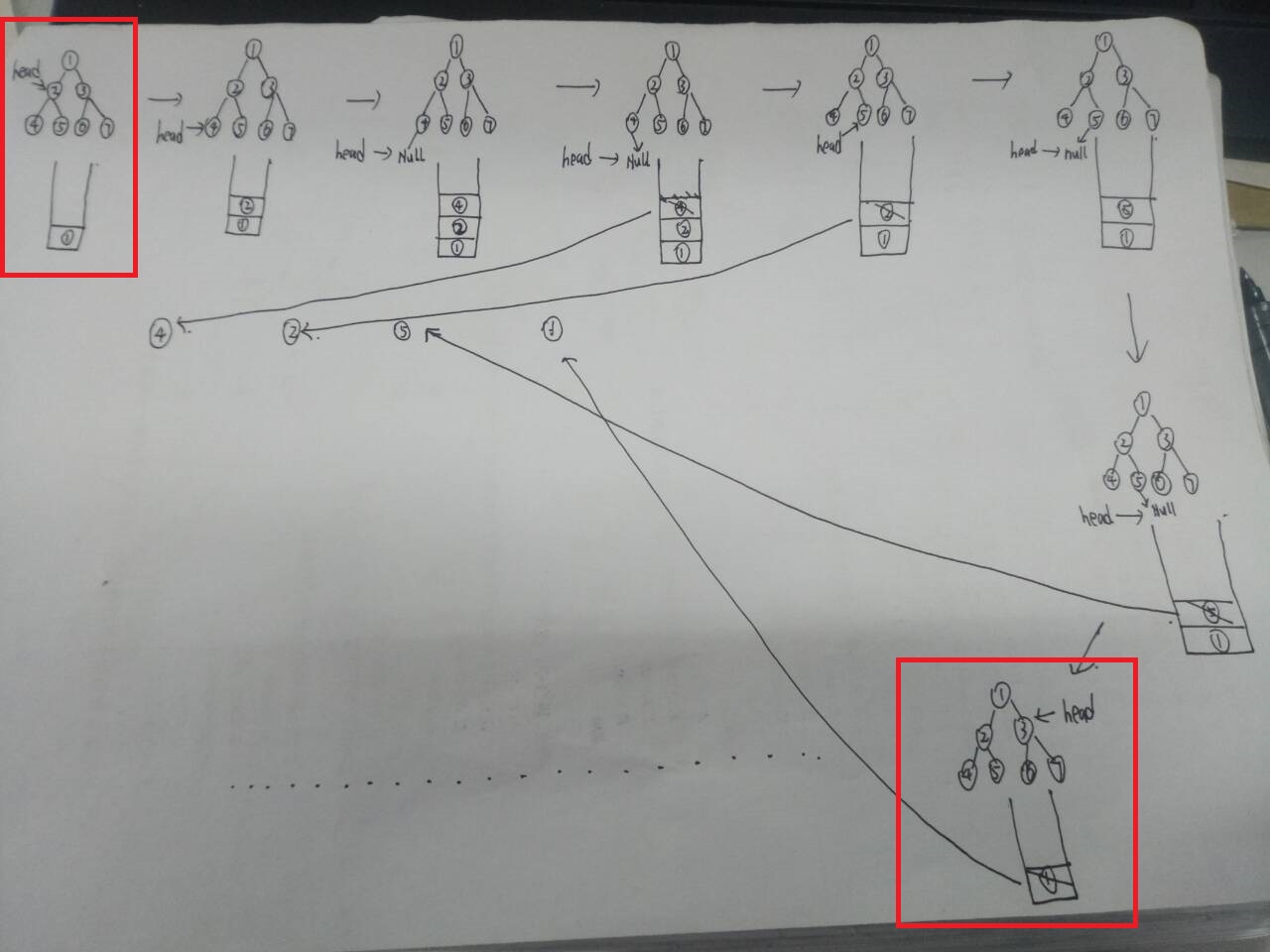
1. 前序遍历的非递归实现

运用了一个栈结构实现。先序遍历的遍历顺序为根节点-->左孩子-->右孩子，所以往栈中放数时先放右孩子，在放左孩子（左右孩子都不为空的情况下）。根据栈的先进后出的性质，所以先打印左孩子再打印右孩子，但是有的人可能会有疑问，那根节点呢。根节点在往栈中放左右孩子的时候就已经打印完了，所以根节点肯定在左右孩子打印之前就打印完了。这样打印顺序就为：根节点-->左孩子-->右孩子。

实现代码如下：

// 前序遍历（非递归方式）
void preorder(BiTree *T)
{
	// 判断二叉树是否存在
	if (T == NULL)
		return;

	stack<BiTree *> stack; // 利用栈结构实现
	stack.push(T); // 将头节点放入栈中去
	while (!stack.empty())
	{
		T = stack.top(); // T指向弹出剩下后的最顶端结点
		stack.pop();
		printf("%c", T->data); // 显示结点数据，可以更改为其它对结点操作
		if (T->rchild != NULL) // 如果右孩子不为空，先放右孩子.
			stack.push(T->rchild);
		if (T->lchild != NULL) // 如果左孩子不为空，后放左孩子，这样才能保证打印顺序为:头节点-->左孩子-->右孩子
			stack.push(T->lchild);
	}
}

代码执行过程如下图所示：

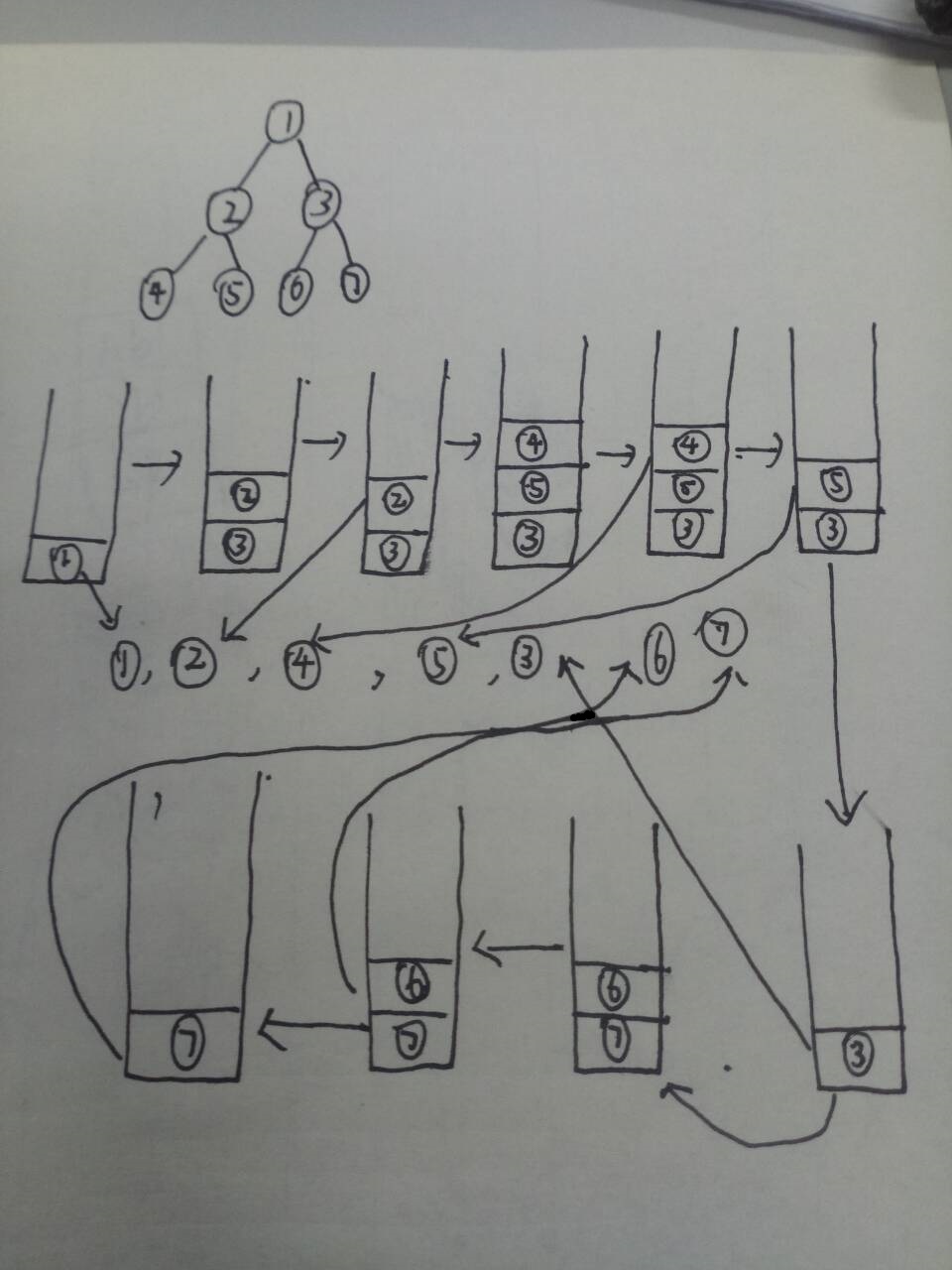
2. 中序遍历的非递归实现

运用了一个栈结构实现。如果当前节点不为空，就往栈中放入该节点，然后让指向该节点的指针指向该节点的左孩子。如果当前节点为空，就弹出栈顶的节点，打印。然后让指向该节点的指针指向该节点的右孩子。

实现代码如下：

// 中序遍历（非递归方式）
void inorder(BiTree *T)
{
	// 判断二叉树是否存在
	if (T == NULL)
		return;

	stack<BiTree *> stack; // 利用栈结构实现
	while (!stack.empty() || T != NULL) // 这两个条件只要满足一个，就执行下面过程
	{
		if (T != NULL) // 如果当前节点不为空，就把当前节点放入栈中去，然后让head指向当前节点的左节点，没有打印过程
		{
			stack.push(T);
			T = T->lchild;
		}
		else if (T == NULL) // 如果当前节点为空，那么就弹出栈顶的元素，打印。然后让head指向栈顶节点的右节点
		{
			T = stack.top();
			stack.pop();
			printf("%c", T->data); // 显示结点数据，可以更改为其它对结点操作
			T = T->rchild;
		}
	}
}

代码执行过程如下图所示：

上面圈的那两个状态是一样的，所以没写的部分和上层圈的那个状态后面的状态是一样的（只不过一个是左子树，一个是右子数）

3. 后序遍历的非递归实现

运用了一个栈结构和 vector 结构实现。最先将根节点数据插入在 vector 的位置 0，然后插入左子树的节点数据在位置0（造成逆序），再插入右子树的节点数据在位置0（也是逆序）。

实现代码如下：

//后序遍历（非递归方式）
void postorder(BiTree *T)
{
	// 判断二叉树是否存在
	if (T == NULL)
		return;

	stack<BiTree *> stack;
	vector<ElemType> vec;
	stack.push(T);

	BiTree *p = nullptr;
	while (!stack.empty())
	{
		p = stack.top();
		stack.pop();
		vec.insert(vec.begin(), p->data); // 一直在位置0插入，则根节点会在vector的最末尾（相当于逆序插入）
		if (p->lchild)
			stack.push(p->lchild);
		if (p->rchild)
			stack.push(p->rchild);
	}

	for (int i = 0; i < vec.size(); i++)
		printf("%c", vec[i]);
}

参考：

如何检测链表中是存在循环

删除链表中重复的节点（经典链表面试题）

二叉树的3种遍历方法 6种实现