JZOJ3492数数&&GDOI2018超级异或绵羊——位&&类欧几里得

JZOJ3492 数数(count)

我们知道，一个等差数列可以用三个数A,B,N表示成如下形式： 
B+A,B+2A,B+3A⋯B+NA
ztxz16想知道对于一个给定的等差数列，把其中每一项用二进制表示后，一共有多少位是1
A<=1e4，B<=1e16，N<=1e12

分析：

有个很经典的类欧套路，k从0开始

二进制下，第k位是否为1，等于(原数>>k)-2*(原数>>(k+1))，

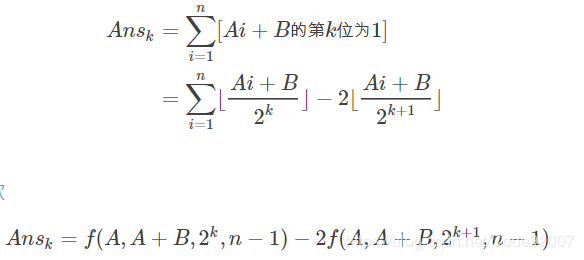
可以把i从1到n变成i从0到n-1，也就是提一个A出来，再做，于是就是类欧板子题。

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

ll f(ll a, ll b, ll c, ll n)
{
    if(!a)  return (b/c)*(n+);
    if(a >= c || b >= c)  return (f(a%c, b%c, c, n) + n*(n+)/*(a/c) + (n+)*(b/c));
    ll m = (a*n+b) / c;
    return (n*m - f(c, c-b-, a, m-));
}

ll a, b, n;

int main()
{
    int T;
    scanf("%d", &T);
    while(T--)
    {
        scanf("%lld%lld%lld", &a, &b, &n);
        ll limit = b + a*n, ans = ;
        for(int mi = ; mi <= limit; mi*=)  ans += f(a, a+b, mi, n-) - f(a, a+b, mi*, n-)*;
        printf("%lld\n", ans);
    }
    return ;
}

【GDOI2018模拟8.8】超级绵羊异或

求(a) xor (a + b) xor (a + b * 2) xor … xor (a + b * (n - 1))。

对于100%的数据，t<=1e4，a, n<=1e9， b<=1e9；

分析：

还是用上面那一个套路，

写成求和形式，考虑最后第k位的奇偶，即像上题一样，判断每一位的出现次数，对每一位使用类欧。

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

ll f(ll a, ll b, ll c, ll n)
{
    if(!a)  return (b/c)*(n+);
    if(a >= c || b >= c)  return (f(a%c, b%c, c, n) + n*(n+)/*(a/c) + (n+)*(b/c));
    ll m = (a*n+b) / c;
    return (n*m - f(c, c-b-, a, m-));
}

ll a, b, n;

int main()
{
    int T;
    scanf("%d", &T);
    while(T--)
    {
        scanf("%lld%lld%lld", &n, &a, &b);
        ll limit = a + b*(n-), ans = ;
        for(int mi = ; mi <= limit; mi*=)
        {
            ll tmp = f(b, a, mi, n-) - f(b, a, mi*, n-)*;
            ans += (tmp&)*mi;
        }
        printf("%lld\n", ans);
    }
    return ;
}

BZOJ3817

给定正整数N，R。求

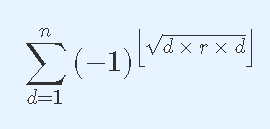
分析：

继续用上面的套路，考虑幂的奇偶会对答案造成不同贡献，本质上是幂的第1位是否为1，即求 $Ans_0$.

因为底数是-1，对布尔式的贡献线性变换一下，搞成1-2*Ans0。

由于sqrt(r)是实数，不能完全当整数处理，

$\begin{align}
f(a,b,c,n) &= \left \lfloor \frac{bx+c}{a} \right \rfloor\frac{n(n+1)}{2} + \sum_{i=1}^{\left \lfloor \frac{bx+d}{a}n \right \rfloor}n-\frac{a}{bx+d}i  \\
&=  \left \lfloor \frac{bx+c}{a} \right \rfloor\frac{n(n+1)}{2}  + \left \lfloor \frac{bx+d}{a} n \right \rfloor n -  \sum_{i=1}^{\left \lfloor \frac{bx+d}{a}n \right \rfloor} \left \lfloor \frac{a}{bx+d}i \right \rfloor
\end{align}$

将后面和式里的东西分母有理化得

$f(a,b,c,n) = S-\sum_{i=1}^{\left \lfloor \frac{bx+d}{a}n \right \rfloor}\left \lfloor \frac{abx-ad}{b^2x^2-d^2}i \right \rfloor = S - f(b^2r-d^2, ab, -ad, \left \lfloor \frac{bx+d}{a}n \right \rfloor)$

于是递归求，类似于辗转相除，递归层数不超过 $log_2n$.

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
ll n, r;
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }

double x;
ll f(ll a, ll b, ll c, ll n)
{
    if(!n)  return ;
    ll t = gcd(a, gcd(b, c)); a/= t, b/=t, c/=t;
    ll d = c - (ll)((b*x+c)/a)*a;
    ll s = (ll)((b*x+c)/a)*(n+)*n/ + n*(ll)((b*x+d)*n/a);
    return s - f(b*b*r-d*d, a*b, -a*d, (ll)((b*x+d)*n/a));
}

int main()
{
    int T;scanf("%d", &T);
    while(T--)
    {
        scanf("%lld%lld", &n, &r);
        x = sqrt(r);
        if(x==(int)(x+0.5))  printf("%lld\n", (r&)? ((n&)? - : ) : n);
        else  printf("%lld\n", n+*f(,,,n)-*f(,,,n));
    }
    return ;
}

参考链接：

1. https://blog.csdn.net/code92007/article/details/97396823

2. https://blog.csdn.net/lych_cys/article/details/51345089

3. https://www.cnblogs.com/xiao-ju-ruo-xjr/p/7157945.html