Kalman Filter、Extended Kalman Filter以及Unscented Kalman Filter介绍

模型定义

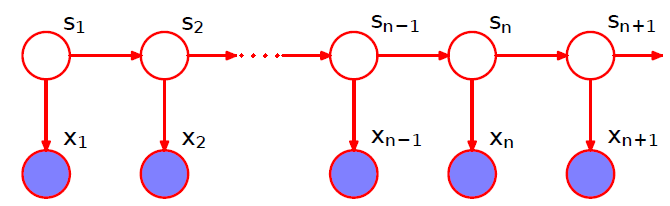
如上图所示，卡尔曼滤波(Kalman Filter)的基本模型和隐马尔可夫模型类似，不同的是隐马尔科夫模型考虑离散的状态空间，而卡尔曼滤波的状态空间以及观测空间都是连续的，并且都属于高斯分布，因此卡尔曼滤波又称为linear Gaussian Markov model，它的数学定义如下：$$\underbrace{s_{t}=C s_{t-1}+G h_{t}+\gamma_{t}}_{\text { latent process }}, \quad \underbrace{x_{t}=D s_{t}+\varepsilon_{t}}_{\text { observed process }}$$其中$h_t$表示控制向量(control vector)，是已知量；$\gamma_{t} \sim N(0, Q)$表示状态误差，它包含了状态转换公式$C s_{t-1}+G h_{t}$中未考虑到的其它因素，是状态转换公式准确性的度量；$\varepsilon_{t} \sim N(0, V)$表示观测误差，是观测精度的度量。下面举一个简单的例子：

假设有一个二维空间上的物体位置的观测序列($x_{t} \in \mathbb{R}^{2}$)，观测有一定误差；该物体的状态$s_t=[p_{t1},v_{t1},p_{t2},v_{t2}]^T$，其中$p_t$和$v_t$表示物体位置和速度，下标1和2表示方向；控制向量为$h_t=[a_{t1},a_{t2}]^T$，$a_t$表示加速度。由基本的物理公式可知$$s_{t}=\underbrace{\left[\begin{array}{cccc}{1} & {\Delta t} & {0} & {0} \\ {0} & {1} & {0} & {0} \\ {0} & {0} & {1} & {\Delta t} \\ {0} & {0} & {0} & {1}\end{array}\right]}_{C}s_{t-1}+\underbrace{\left[\begin{array}{cc} \frac{1}{2}(\Delta t)^{2} & {0} \\ {\Delta t} & {0} \\ {0} & \frac{1}{2}(\Delta t)^{2} \\ {0} & {\Delta t}\end{array}\right]}_{G}h_t+\gamma_t\text{ 以及 }x_{t}=\underbrace{\left[\begin{array}{cccc}{1} & {0} & {0} & {0} \\ {0} & {0} & {1} & {0}\end{array}\right]}_{D}s_{t}+\varepsilon_{t}$$

卡尔曼滤波的目标是已知观测序列$x_1,x_2,\cdots,x_t$，计算当前隐藏状态的分布函数，即$$s_{t}\left|s_{t-1} \sim N\left(C s_{t-1}+G h_{t}, Q\right), \quad x_{t}\right| s_{t} \sim N\left(D s_{t}, V\right)\quad
\Rightarrow\quad p\left(s_{t} | x_{1}, \dots, x_{t}\right);\quad 1\leq t \leq T$$注意除观测序列以外，矩阵$C,G,Q,D,V$以及控制向量$h_t$也是给定的。

模型求解

定义$S_t=(s_{t} | x_{1}, \ldots, x_{t})$，容易看出$S_t$满足高斯分布$N(\mu_{t}, \Sigma_{t})$，$\mu_t$以及$\Sigma_t$即为需要求解的量
- 为方便之后的计算，令$S_{t-1}=(s_{t-1} | x_{1}, \ldots, x_{t-1})=\underbrace{\mu_{t-1}}_\text{mean}+\Delta S_{t-1},\quad \Delta S_{t-1} \sim N(0,\Sigma_{t-1})$
定义$P_t= (s_{t} | x_{1}, \ldots, x_{t-1})$，有$P_t=CS_{t-1}+G h_{t}+\gamma_{t}$
- 为方便之后的计算，令$P_t=\underbrace{C\mu_{t-1}+Gh_t}_{\mu_{P_t}}+\underbrace{C\Delta S_{t-1}+\gamma_t}_{\Delta P_t}$
定义$O_t= (x_{t} | x_{1}, \ldots, x_{t-1})$，有$O_t=DP_{t}+\varepsilon_t$
- 为方便之后的计算，令$O_t=\underbrace{D(C\mu_{t-1}+Gh_t)}_{\mu_{O_t}}+\underbrace{DC\Delta S_{t-1}+D\gamma_t+\varepsilon_t}_{\Delta O_t}$

由上述定义可知 $$\left[\begin{array}{c} P_t \\ O_t \end{array}\right] \sim N\left(\left[\begin{array}{c} \mu_{P_t} \\ \mu_{O_t} \end{array}\right], \left[\begin{array}{cc} \Sigma_{PP} & \Sigma_{PO}\\ \Sigma_{PO}^T & \Sigma_{OO} \end{array}\right] \right)$$接下来计算协方差矩阵的这些项：

$\Sigma_{PP}=\mathbb{E}[{\Delta P_t (\Delta P_t)^T}]=C\mathbb{E}[\Delta S_{t-1} (\Delta S_{t-1})^T]C^T+\mathbb{E}[\gamma_t\gamma_t^T]=C\Sigma_{t-1}C^T+Q$
$\Sigma_{PO}=\mathbb{E}[{\Delta P_t (\Delta O_t)^T}]=C\mathbb{E}[\Delta S_{t-1} (\Delta S_{t-1})^T]C^TD^T+\mathbb{E}[\gamma_t\gamma_t^T]D^T=C\Sigma_{t-1}C^TD^T+QD^T$
$\Sigma_{OO}=\mathbb{E}[{\Delta O_t (\Delta O_t)^T}]=DC\mathbb{E}[\Delta S_{t-1} (\Delta S_{t-1})^T]C^TD^T+D\mathbb{E}[\gamma_t\gamma_t^T]D^T+\mathbb{E}[\varepsilon_t\varepsilon_t^T]=DC\Sigma_{t-1}C^TD^T+DQD^T+V$

容易看出$S_t=(P_t | O_t)$，此外定义$$\hat{\mu}_t=\mu_{P_t}=C \mu_{t-1}+Gh_t，\text{ }\hat{\Sigma}_t=\Sigma_{PP}=C \Sigma_{t-1} C^{T}+Q\text{以及卡尔曼增益矩阵}K_t=\hat{\Sigma}_{t}D^T[D\hat{\Sigma}_{t}D^T+V]^{-1}$$由高斯分布的性质可知

$\Sigma_t=\Sigma_{PP}-\Sigma_{PO}\Sigma_{OO}^{-1}\Sigma_{PO}^T=(I-K_tD)\hat{\Sigma}_t$
$\mu_t=\mu_{P_t}+\Sigma_{PO}\Sigma_{OO}^{-1}(O_t-\mu_{O_t})=\hat{\mu}_t+K_t(x_t-D\hat{\mu}_t)$

上述求解过程可归纳为：

初始化$\mu_0$以及$\Sigma_0$
预测：$\hat{\mu}_t=C \mu_{t-1}+Gh_t$以及$\hat{\Sigma}_t=C \Sigma_{t-1} C^{T}+Q$
计算卡尔曼增益矩阵$K_t=\hat{\Sigma}_{t}D^T[D\hat{\Sigma}_{t}D^T+V]^{-1}$
更新：$\mu_t=\hat{\mu}_t+K_t(x_t-D\hat{\mu}_t)$以及$\Sigma_t=(I-K_tD)\hat{\Sigma}_t$

Extended Kalman Filter

在Extended Kalman Filter中，状态之间的转化以及状态向观测的转化是非线性的，即$$s_t=g(s_{t-1},h_t)+\gamma_t,\text{ }x_{t}=f(s_{t})+\varepsilon_{t};\text{ 其中}g,f\text{代表非线性函数}$$此时考虑使用泰勒公式将非线性函数近似为线性函数，延续上一部分的定义，有

$P_t=g(S_{t-1},h_t)+\gamma_{t}=g(\mu_{t-1}+\delta S_{t-1},h_t)+\gamma_{t}=\underbrace{g(\mu_{t-1},h_t)}_{\mu_{P_t}(\text{i.e., }\hat{\mu}_t)}+\underbrace{J_g\Delta S_{t-1}+\gamma_{t}}_{\Delta P_t}$
$O_t=h(P_t)+\varepsilon_t=f(\mu_{P_t}+\Delta P_t)+\varepsilon_t=f(\mu_{P_t})+J_f\Delta P_t+\varepsilon_t=\underbrace{f(\hat{\mu}_{t})}_{\mu_{O_t}}+\underbrace{J_fJ_g\Delta S_{t-1}+J_f\gamma_t+\varepsilon_t}_{\Delta O_t}$

其中$J_g$和$J_f$为Jacobian矩阵，假设状态为$m$维向量，观测为$n$维向量，并且$g(s,h)=[g_1(s,h),\cdots,g_m(s,h)]^T$以及$f(s)=[f_1(s),\cdots,f_n(s)]^T$，则有$$J_g=\left[\begin{array}{cccc}\frac{\partial g_1}{\partial \mu_{t-1,1}} & \frac{\partial \mu_1}{\partial s_{t-1,2}} & \cdots & \frac{\partial g_1}{\partial \mu_{t-1,m}} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{\partial g_m}{\partial \mu_{t-1,1}} & \frac{\partial g_m}{\partial \mu_{t-1,2}} & \cdots & \frac{\partial g_m}{\partial \mu_{t-1,m}}\end{array}\right], \text{ }J_f=\left[\begin{array}{cccc}\frac{\partial f_1}{\partial \hat{\mu}_{t,1}} & \frac{\partial f_1}{\partial \hat{\mu}_{t,2}} & \cdots & \frac{\partial f_1}{\partial \hat{\mu}_{t,m}} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{\partial f_n}{\partial \hat{\mu}_{t,1}} & \frac{\partial f_n}{\partial \hat{\mu}_{t,2}} & \cdots & \frac{\partial f_n}{\partial \hat{\mu}_{t,m}}\end{array}\right]$$容易看出Extended Kalman Filter的求解过程可归纳为：

初始化$\mu_0$以及$\Sigma_0$
预测：$\hat{\mu}_t=g(\mu_{t-1},h_t)$以及$\hat{\Sigma}_t=J_g \Sigma_{t-1} J_g^{T}+Q$
计算卡尔曼增益矩阵$K_t=\hat{\Sigma}_{t}J_f^T[J_f\hat{\Sigma}_{t}J_f^T+V]^{-1}$
更新：$\mu_t=\hat{\mu}_t+K_t[x_t-f(\hat{\mu}_t)]$以及$\Sigma_t=(I-K_tJ_f)\hat{\Sigma}_t$

Unscented Kalman Filter

Unscented Kalman Filter和Extended Kalman Filter的模型定义一样，只是具体求解方法不同。相对于Extended Kalman Filter使用泰勒公式近似非线性函数，Unscented Kalman Filter通过选取多个样本点(the sigma points)直接估计均值和方差。仍然延续之前的定义，假设状态为$m$维向量，从随机变量$S_{t-1}$中选取$2m+1$个样本点，记为矩阵$\mathcal{X}_{t-1}$($m$行$2m+1$列)，选取方式为$$\mathcal{X}_{t-1}=\left[\begin{array}{ccc}\mu_{t-1} & \mu_{t-1}+\sqrt{(m+\lambda )\Sigma_{t-1}} & \mu_{t-1}-\sqrt{(m+\lambda )\Sigma_{t-1}} \end{array}\right]$$若将$\Sigma_{t-1}$进行Cholesky分解得到$LL^T$，则$\sqrt{\Sigma_{t-1}}=L$；或者对$\Sigma_{t-1}$进行特征值分解得到$U\Lambda U^T$(其中$\Lambda$为对角阵)，则$\sqrt{\Sigma_{t-1}}=U\Lambda^{1/2}$。接下来对每个采样点分配权重：

$\vec{w}_a=\left[\begin{array}{ccccc}\frac{\lambda}{m+\lambda} & \frac{1}{2(m+\lambda)} & \frac{1}{2(m+\lambda)} & \cdots & \frac{1}{2(m+\lambda)}\end{array}\right]$
$\vec{w}_c=\left[\begin{array}{ccccc}\frac{\lambda}{m+\lambda}+(1-\alpha^2+\beta) & \frac{1}{2(m+\lambda)} & \frac{1}{2(m+\lambda)} & \cdots & \frac{1}{2(m+\lambda)}\end{array}\right]$

其中$\vec{w}_a$为求均值时的权重，$\vec{w}_c$为求协方差矩阵时的权重。针对一些参数的取值有以下建议：$$\alpha \in (0,1],\text{ }\beta=2,\text{ }\lambda=\alpha^2(m+\kappa)-m,\text{ }\kappa\geq 0$$将$\mathcal{X}_{t-1}$代入函数$g$可以得到$$\hat{\mathcal{X}}_{t}=\left[\begin{array}{cccc}g(\mathcal{X}_{t-1}^{[1]},h_t) & g(\mathcal{X}_{t-1}^{[2]},h_t) & \cdots & g(\mathcal{X}_{t-1}^{[2m+1]},h_t)\end{array}\right]$$其中上标表示矩阵的列数，由$\hat{\mathcal{X}}_{t}$可以估计出$\hat{\mu}_t$以及$\hat{\Sigma}_t$，接下来可以通过两种方式得到观测的采样点$\mathcal{Z}_t$：

直接通过$\hat{\mathcal{X}}_{t}$进行计算，即$$\mathcal{Z}_{t}=\left[\begin{array}{cccc}h(\hat{\mathcal{X}}_{t}^{[1]}) & h(\hat{\mathcal{X}}_{t}^{[2]}) & \cdots & h(\hat{\mathcal{X}}_{t}^{[2m+1]}) \end{array}\right]$$
通过得到的$\hat{\mu}_t$以及$\hat{\Sigma}_t$重新采样，有公式$$\hat{\mathcal{X}}_{t}^*=\left[\begin{array}{ccc}\hat{\mu}_{t} & \hat{\mu}_{t}+\sqrt{(m+\lambda )\hat{\Sigma}_{t}} & \hat{\mu}_{t}-\sqrt{(m+\lambda )\hat{\Sigma}_{t}} \end{array}\right]$$然后计算过程同第一种方式，即$$\mathcal{Z}_{t}=\left[\begin{array}{cccc}h(\hat{\mathcal{X}}_{t}^{*[1]}) & h(\hat{\mathcal{X}}_{t}^{*[2]}) & \cdots & h(\hat{\mathcal{X}}_{t}^{*[2m+1]}) \end{array}\right]$$

最后估计观测的均值和协方差矩阵，进而得到最终的结果，Unscented Kalman Filter的求解过程可归纳为：

初始化$\mu_0$以及$\Sigma_0$
预测：$\hat{\mu}_t=\sum_{j=1}^{2m+1}w_{aj}\hat{\mathcal{X}}_{t}^{[j]}$以及$\hat{\Sigma}_t=\sum_{j=1}^{2m+1}w_{cj}(\hat{\mathcal{X}}_{t}^{[j]}-\hat{\mu}_t)(\hat{\mathcal{X}}_{t}^{[j]}-\hat{\mu}_t)^T+Q$
计算$\mathcal{Z}_{t}$（从上述两种方式中选择一种），得到$\mu_{O_t}=\sum_{j=1}^{2m+1}w_{aj}\mathcal{Z}_{t}^{[j]}$以及$\Sigma_{OO}=\sum_{j=1}^{2m+1}w_{cj}({\mathcal{Z}}_{t}^{[j]}-\mu_{O_t})({\mathcal{Z}}_{t}^{[j]}-\mu_{O_t})^T+V$
计算$\Sigma_{PO}=\sum_{j=1}^{2m+1}w_{cj}(\hat{\mathcal{X}}_{t}^{[j]}-\hat{\mu}_{t})({\mathcal{Z}}_{t}^{[j]}-\mu_{O_t})^T$，注意若使用第二种方式计算$\mathcal{Z}$，需将公式中的$\hat{\mathcal{X}}_{t}$替换为$\hat{\mathcal{X}}_{t}^*$
计算卡尔曼增益矩阵$K_t=\Sigma_{PO}\Sigma_{OO}^{-1}$
更新：$\mu_t=\hat{\mu}_t+K_t[x_t-\mu_{O_t}]$以及$\Sigma_t=\hat{\Sigma}_t-\Sigma_{PO}\Sigma_{OO}^{-1}\Sigma_{PO}^T=\hat{\Sigma}_t-K_t\Sigma_{OO}K_t^T$