skkyk:点分治

由题开始==

例题：求在一棵有权树上，是否存在一条路径满足权值和为K

解法：以每个点为根一次，看在他的子树间是否存在两段，其和为K;O(==)

和例题一样，对于树上问题，求某些要求的路径(数量或者存在性等)，

往往可以先对一条经过根节点的路径操作，

后再删去这个根，对他的子树们同样的操作

显然是一个分治过程

原理就是，一条路径，要么是由一个点经过根节点，与其他子树内的节点形成；

要么就是只在这棵子树内形成路径

大概图示意思（红绿为两条上述路径）



<

当我们的树比较平衡时，每个点被路径计算是$ logn $ 的，但是当树是一条链的时候，就退化成$ n^2 $ 了

为了避免这种情况，可以用树的重心代替，成为新的根。此时总复杂度为$ O (nlogn) 。$

原因就是，一棵树，怎么为根都还是一颗树，但是以重心为根的时候，这颗树是最好看的最平衡的

rt，将链按箭头提起来:





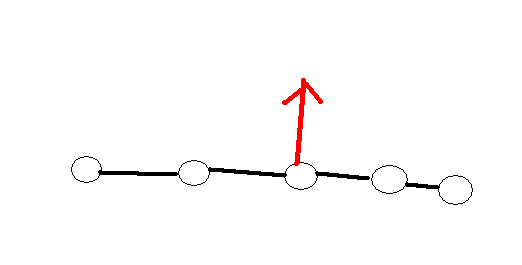
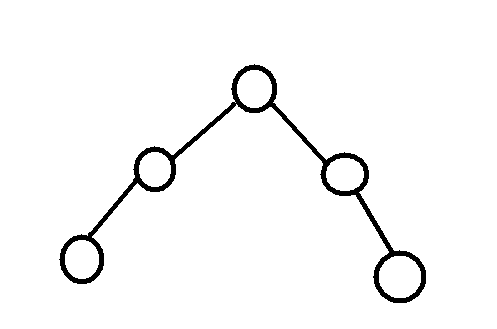
这看向去更像是一棵树

。

所以

总结一下

一棵树先确定他的重心，以重心为根，确定经过根节点的路径；再把根节点删掉，对于删掉他的子树们，按上述同样操作；

已证$ O(nlogn) $。

luogu模板题代码仅供参考，不解释。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e4+50;
const int K = 1e7+50;
int n,m;
struct node{int next,to,dis;}edge[N<<1];
int head[N],cnt;
inline void add(int from,int to,int dis) {
	edge[++cnt].to=to,edge[cnt].dis=dis,edge[cnt].next=head[from],head[from]=cnt;
}
int q[N],ans[N],maxp[N],size[N],visited[N],tmp[N],dis[N],judge[K];
int rt,sum,tot;
void getrt(int u,int f) {
	size[u]=1,maxp[u]=0;
	for(int i=head[u];i;i=edge[i].next) {
		int v=edge[i].to;if(v==f||visited[v]) continue;
		getrt(v,u);
		size[u]+=size[v];maxp[u]=max(maxp[u],size[v]);
	}
	maxp[u]=max(maxp[u],sum-maxp[u]);
	if(maxp[u]<maxp[rt]) rt=u;//要求最大的最小
}
void getdis(int u,int f) {
	tmp[++tot]=dis[u];
	for(int i=head[u];i;i=edge[i].next) {
		int v=edge[i].to;if(v==f||visited[v]) continue;
		dis[v]=dis[u]+edge[i].dis; getdis(v,u);
	}
}
queue<int> que;
void solve(int u) {
	for(int i=head[u];i;i=edge[i].next) {
		int v=edge[i].to;if(visited[v]) continue;
		dis[v]=edge[i].dis;
		tot=0;getdis(v,u);
		for(int j=1;j<=tot;j++)
			for(int k=1;k<=m;k++)
				if(q[k]>=tmp[j])
					ans[k]|=judge[q[k]-tmp[j]];
		for(int j=1;j<=tot;j++) que.push(tmp[j]),judge[tmp[j]]=1;
	}
	while(!que.empty()) judge[que.front()]=0,que.pop();//数组过大，memset超时
}
void divide(int u) {
	judge[0]=visited[u]=1;solve(u);
	for(int i=head[u];i;i=edge[i].next) {
		int v=edge[i].to;if(visited[v]) continue;
		maxp[rt=0]=sum=size[v];
		getrt(v,0),getrt(rt,0);
		divide(rt);
	}
}
int main() {
	cin>>n>>m;
	for(int i=1;i<n;i++) {	int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,c),add(b,a,c);}
	for(int i=1;i<=m;i++) scanf("%d",q+i);
	maxp[rt=0]=sum=n;//初始化
	getrt(1,0),getrt(rt,0);//找重心
	divide(rt);//点分治
	for(int i=1;i<=m;i++) if(ans[i]) puts("AYE");else puts("NAY");
	return 0;
}