[Algorithm] Heap & Priority queue

这里只是简单的了解，具体内容详见推荐的原链接

注意堆和树的区别

堆就是优先级队列的实现形式

---

堆排序

排序过程

Ref: 排序算法之堆排序（Heapsort）解析

• 第一步（构造初始堆）：

{7, 5, 6, 1, 3, 2, 4}已经满足了大根堆，第一步完成

• 第二步（首尾交换，断尾重构）：

• 第三步（重复第二步，直至所有尾巴都断下来）

堆的介绍

Ref: 数据结构：堆（Heap）

STL的 Heap

Outline

Ref: 随笔分类 - 数据结构_算法【博主写得很卖力】

• 二叉堆(一)之 图文解析 和 C语言的实现
• 左倾堆(一)之 图文解析 和 C语言的实现
• 斜堆(一)之 C语言的实现
• 二项堆(一)之 图文解析 和 C语言的实现
• 斐波那契堆(一)之 图文解析 和 C语言的实现

FAQ: Why is the C++ STL priority queue implemented using a binary heap instead of a Fibonacci heap?

Fibonacci heap is better than Binary heap just theoretically.

Because Binary heap is way faster than the Fibonacci heap.

A binary heap is just an array and the methods used are quite simple.

实现 "优先级队列" 的堆

二叉堆

二叉堆是完全二元树或者是近似完全二元树，它分为两种：最大堆和最小堆。

堆 (优先级队列) 的合并

左倾堆

目的

当优先队列中涉及到"对两个优先队列进行合并"的问题时，二叉堆的效率就无法令人满意了，而本文介绍的左倾堆，则可以很好地解决这类问题。

特点

不满节点：是指该该节点的左右孩子至少有一个为NULL。叶节点的NPL为0，NULL节点的NPL为-1。

零距离(英文名NPL，即Null Path Length)：则是从一个节点到一个"最近的不满节点"的路径长度

性质

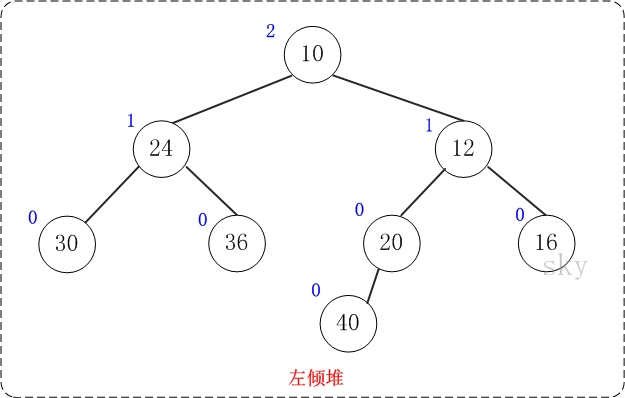
[性质1] 节点的键值小于或等于它的左右子节点的键值。
[性质2] 节点的左孩子的NPL >= 右孩子的NPL。[故谓之“左倾”]
[性质3] 节点的NPL = 它的右孩子的NPL + 1。

斜堆

斜堆是左式堆的自调节形式，左式堆和斜堆的关系类似于伸展树和AVL树的关系。

斜堆具有堆序的性质，但是没有结构的限制，这样的话一次的操作最坏的情况时O(n)，但是连续m次操作总的复杂度O(mlogn)。

二项堆

二项树是一种递归定义的有序树。它的递归定义如下：
(01) 二项树B₀只有一个结点；
(02) 二项树B_k由两棵二项树B_(k-1)组成的，其中一棵树是另一棵树根的最左孩子。

二项堆的性质

[性质一] B_k共有2^k个节点。
[性质二] B_k的高度为k。
[性质三] B_k在深度i处恰好有C_(k,i)个节点，其中i=0,1,2,...,k。
[性质四] 根的度数为k，它大于任何其它节点的度数。

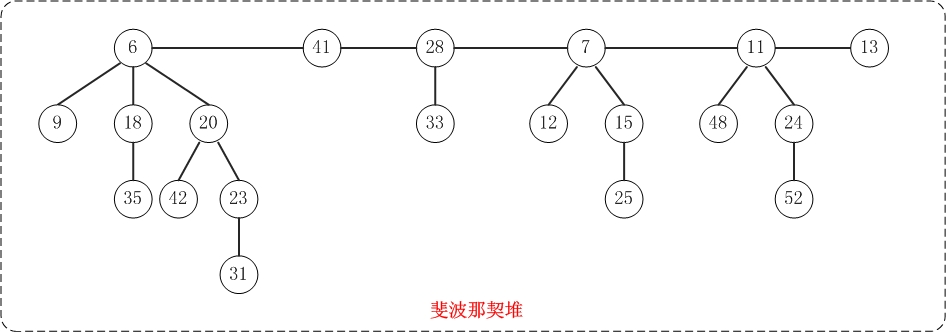
斐波那契堆 (Fibonacci heap)

堆中一种，它和二项堆一样，也是一种可合并堆；可用于实现合并优先队列。

更好的平摊分析性能

斐波那契堆比二项堆具有更好的平摊分析性能，它的合并操作的时间复杂度是O(1)。
与二项堆一样，它也是由一组堆最小有序树组成，并且是一种可合并堆。
与二项堆不同的是，斐波那契堆中的树不一定是二项树；而且二项堆中的树是有序排列的，但是斐波那契堆中的树都是有根而无序的。

End.