2019年牛客多校第一场 B题 Integration 数学

题目链接

传送门

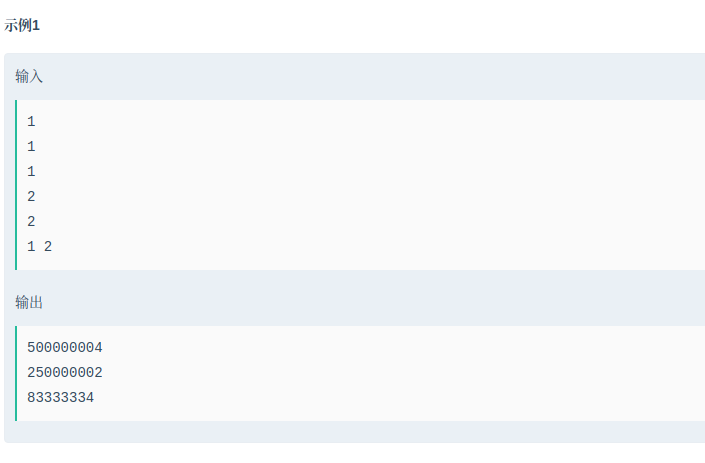
题目

思路

首先我们对\(\int_{0}^{\infty}\frac{1}{\prod\limits_{i=1}^{n}(a_i^2+x^2)}dx\)进行裂项相消：

\[\begin{aligned}
&\frac{1}{\prod\limits_{i=1}^{n}(a_i^2+x^2)}&\\
=&\frac{1}{(a_1^2+x^2)(a_2^2+x^2)}\times\frac{1}{\prod\limits_{i=3}^{n}(a_i^2+x^2)}&\\
=&\frac{1}{a_2^2-a_1^2}\times(\frac{1}{a_1^2+x^2}-\frac{1}{a_2^2+x^2})\times\frac{1}{\prod\limits_{i=3}^{n}(a_i^2+x^2)}&\\
=&\frac{1}{a_2^2-a_1^2}\times(\frac{1}{a_1^2+x^2}\times\frac{1}{a_3^2+x^2}-\frac{1}{a_2^2+x^2}\times\frac{1}{a_3^2+x^2})\times\frac{1}{\prod\limits_{i=4}^{n}(a_i^2+x^2)}&\\
=&\dots&
\end{aligned}
\]

依次裂项相消，然后看系数的规律，可以手动推\(n=2,3\)的系数看规律，也可以计算，比赛的时候我\(n=3\)推到一半队友看到式子和我说这个他学过然后把系数告诉我就\(A\)了(队友\(txdy\))。

每个\(\frac{1}{a_i^2+x^2}\)的系数为\(\frac{1}{\prod\limits_{j=1,j\not=i}^{n}(a_j^2-a_i^2)}\)，因此最后题目要求的式子久变成了下式：

\[\begin{aligned}
&\sum\limits_{i=1}^{n}\frac{1}{\prod\limits_{j=1,j\not=i}^{n}(a_j^2-a_i^2)}\int_0^{\infty}\frac{1}{a_i^2+x^2}dx&\\
=&\sum\limits_{i=1}^{n}\frac{1}{\prod\limits_{j=1,j\not=i}^{n}(a_j^2-a_i^2)\times a_i^2}\int_0^{\infty}\frac{1}{1+(\frac{x}{a_i})^2}dx&\\
=&\sum\limits_{i=1}^{n}\frac{1}{\prod\limits_{j=1,j\not=i}^{n}(a_j^2-a_i^2)\times a_i}\int_0^{\infty}\frac{1}{1+(\frac{x}{a_i})^2}d\frac{x}{a_i}&
\end{aligned}
\]

积分符号里面的东西就是题目给的式子得到\(\frac{\pi}{2}\)，因此最后答案为

\[\begin{aligned}
&\sum\limits_{i=1}^{n}\frac{1}{2\times\prod\limits_{j=1,j\not=i}^{n}(a_j^2-a_i^2)\times a_i}
\end{aligned}
\]

代码实现如下

#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <cassert>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;

typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;

#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) x&(-x)
#define name2str(name) (#name)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]" <<endl
#define FIN freopen("D://Code//in.txt","r",stdin)
#define IO ios::sync_with_stdio(false),cin.tie(0)

const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 1e5 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3fLL;

int n;
int a[maxn], inv[maxn], cnt[maxn];

LL qpow(LL x, int n) {
    LL res = 1;
    while(n) {
        if(n & 1) res = res * x % mod;
        x = x * x % mod;
        n >>= 1;
    }
    return res;
}

int main() {
    int tmp = qpow(2, mod - 2);
    while(~scanf("%d", &n)) {
        for(int i = 1; i <= n; ++i) {
            scanf("%d", &a[i]);
        }
        for(int i = 1; i <= n; ++i) {
            cnt[i] = 1;
            for(int j = 1; j <= n; ++j) {
                if(i == j) continue;
                cnt[i] = 1LL * cnt[i] * ((1LL * a[j] * a[j] % mod - 1LL * a[i]* a[i] % mod) % mod + mod) % mod;
            }
            cnt[i] = qpow(cnt[i], mod - 2);
            cnt[i] = 1LL * cnt[i] * qpow(a[i], mod - 2) % mod;
            cnt[i] = 1LL * cnt[i] * tmp % mod;
        }
        LL ans = 0;
        for(int i = 1; i <= n; ++i) {
            ans = ((ans + cnt[i]) % mod + mod) % mod;
        }
        printf("%lld\n", ans);
    }
    return 0;
}