[hdu-6395]Sequence 分块+矩阵快速幂

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6395

因为题目数据范围太大，又存在递推关系，用矩阵快速幂来加快递推。

每一项递推时  加的下取整的数随着n变化，但因为下取整有连续性（n一段区间下取整的数是相同的），可以分块，相同的用矩阵快速幂加速

想了好久。。如果最小的开始的值是【p/i】的数为i，那连续的一段长度是【p/（p/i）】-i+1，但为什么分段数是根号n级别啊？。。。

套矩阵快速幂，时间复杂度O(sqrt(n) * log(n))

⎧⎩⎨⎪⎪⎪⎪⎪⎪F1F2Fn===ABC⋅Fn−2+D⋅Fn−1+⌊Pn⌋

⎧⎩⎨⎪⎪⎪⎪⎪⎪F1F2Fn===ABC⋅Fn−2+D⋅Fn−1+⌊Pn⌋

一个递推关系式可以用矩阵乘法来表示递推关系

有两种写法

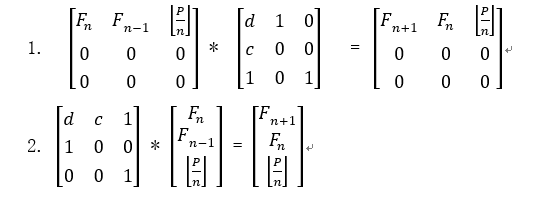
至于怎么求特征值矩阵（用来加速的那个矩阵），就是根据关系式，观察前后两个的变化与联系填就好了

为了写着省事用了第一种，但其实它复杂度高，推荐第二种

坑：

1.n=1 和 n=2 要特判

2.如果n>p，最后加的下取整的数为0，要特判，且特判的时候，注意长度不是【n-p】，p可能比2小，而我们矩阵的第一项是从F₂ 开始的，应为[n-max(2,p)]

3.矩阵快速幂三层循环的变量不要写错，。。一开始把第三层的k写成 i 死循环了

4.运算符重载后不要用scanf输入，在一些oj上会超时

5.max、min函数比较的是同一种变量

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
typedef long long ll;
const int p=1e9+;
ll aa,b,c,d,mo,n;
struct matrix
{
    ll a[][];
    ll* operator [](int x) {return a[x];}//这里是*不是&
    matrix operator *(matrix b)//重载*运算符
    {
        matrix c;
        memset(c.a,,sizeof(c.a));
        ll tmp;
        for (int i=;i<=;i++) {
            tmp=;
            for (int j=;j<=;c[i][j]=tmp%p,tmp=,j++)
            for (int k=;k<=;k++) tmp+=(a[i][k]*b[k][j])%p;
        }
            //前提p^3不爆LL可以在第二层再取模
        return c;
    }
    matrix operator ^(ll T)
    {
        matrix a=*this,b;//this是指针，所以是*this，这样才可以保证原来的a并不改变
        memset(b.a,,sizeof(b.a));
        for (int i=;i<=;i++) b[i][i]=;
        for (;T;a=a*a,T>>=) if (T&) b=b*a;
        return b;
    }
};
matrix ans;
void work(ll ci,ll chang){
    ans[][]=chang;
    matrix node;
     node[][]=d,node[][]=,node[][]=;
     node[][]=c,node[][]=,node[][]=;
     node[][]=,node[][]=,node[][]=;
     matrix ping=node^ci;
     ans=ans*ping;
}
int main(){
    int t;
    scanf("%d",&t);
    for(int p=;p<=t;p++){
        cin>>aa>>b>>c>>d>>mo>>n;
       if(n==){
           cout<<aa;continue;//运算符重载后不要用scanf输入
       }
       else if(n==){
           cout<<b;continue;
       }
       else{

        ans[][]=b,ans[][]=aa;
        for(int i=;i<=;i++){
           ans[][i]=;ans[][i]=;
        }
        for(ll i=,j;i<=n;i=j+){
               if(mo/i==)break;
            j=mo/(mo/i);
               if(n<j)j=n;
            work(j-i+,mo/i);
        }
           ll w=;
           if(mo>w)w=mo;
           if(n>mo)work(n-w,);//一定不要直接用n-mo，如果mo是1会错误，要与2进行大小比较
           cout<<ans[][]<<endl;
       }
    }
    return ;
}

再附上一个矩阵快速幂的板子：

struct matrix
{
    int n,m;
    LL a[maxk][maxk];
    LL* operator [](int x) {return a[x];}//这里是*不是&
    matrix operator *(matrix b)
    {
        int i,j,kk;
        matrix c;
        c.n=n,c.m=b.m;
        memset(c.a,,sizeof(c.a));
        LL tmp;
        for (i=;i<=n;i++) for (j=,tmp=;j<=b.m;c[i][j]=tmp%p,tmp=,j++)
            for (kk=;kk<=m;kk++) tmp+=a[i][kk]*b[kk][j];
        return c;
    }
    matrix operator ^(LL T)
    {
        matrix a=*this,b;//this是指针，所以是*this，这样才可以保证原来的a并不改变
        memset(b.a,,sizeof(b.a));
        b.n=n,b.m=m;
        for (int i=;i<=n;i++) b[i][i]=;
        for (;T;a=a*a,T>>=) if (T&) b=b*a;
        return b;
    }
};
/*
ll* 返回的是指针，也就是 a[x]是一个指针（相当于返回第x行第0列的数值的指针），a[x][y]是一个数值，在外面调用a[x][y]时，相当于(m.a[x])[y]

F1F2Fn===ABC⋅Fn−2+D⋅Fn−1+⌊Pn⌋