POJ 1390 Blocks (区间DP) 题解

题意

t组数据，每组数据有n个方块，给出它们的颜色，每次消去的得分为相同颜色块个数的平方(要求连续)，求最大得分。

首先看到这题我们发现我们要把大块尽可能放在一起才会有最大收益，我们要将相同颜色块合在一起，我们可以分区间进行处理，便可用区间dp解决，我们尝试合并区间我们定义状态f[i][j]表示合并i-j这个区间的最大得分,那么状态转移方程便可写为

f[i][j]=max(f[i][j],f[i][u]+f[v][j]+(v-u+1)^2)（i=<u,v<=j）

我们可以发现我们这样去做不一定就是最优的，因为我们可以通过操作使颜色块数量增加。

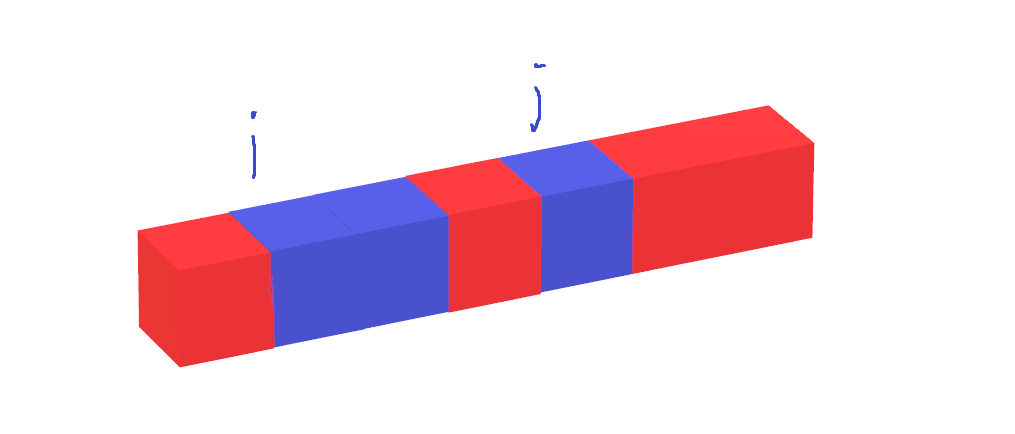
如图我们发现如果按照前面设计的状态转移方程来消去是不合理的，因为我们可以将外面的容纳进来再进行消去会获得更大的收益

此时dp不满足，我们可以考虑再加入一个维度，定义f[i][j][k]表示代表合并区间[i, j]内的颜色块，并且有k个颜色块与j颜色块相同的最大得分。

1：先把第j个颜色块和后面的k个颜色块合并了。

2：先不急着合并，看一看[i, j - 1]中有没有与j颜色相同的，如果有（假设这个和j颜色相同的颜色块是p),那么先把[p, j - 1]合并了。

此时状态转移方程为

f[i][j][k]=f[i][j-1][0]+(len[j]+k)^2(len为颜色相同的长度)

f[i][j][k]=f[i][p][k+len[j]]+f[p+1][j-1][0]。

结合范围取最大值即可

#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
int T,n,dp[210][210][210];
int c[210],len[210],tot;
int solve(int l,int r,int k){
	if(dp[l][r][k]) return dp[l][r][k];
	if(l==r) return (len[r]+k)*(len[r]+k);
	dp[l][r][k]=solve(l,r-1,0)+(len[r]+k)*(len[r]+k);
	for(int i=l;i<r;++i){
		if(c[i]==c[r]){
			dp[l][r][k]=max(dp[l][r][k],solve(l,i,len[r]+k)+solve(i+1,r-1,0));
		}
	}
	return dp[l][r][k];
}
int main(){
	scanf("%d",&T);
	for(int t=1;t<=T;++t){
		scanf("%d",&n);
		int x,now=-1;
		tot=0;
		memset(dp,0,sizeof(dp));
		memset(len,0,sizeof(len));
		for(int i=1;i<=n;++i){
			scanf("%d",&x);
			if(x==now){
				len[tot]++;
			}
			else{
				c[++tot]=x;
				len[tot]++;
				now=x;
			}
		}
		printf("Case %d: %d\n",t,solve(1,tot,0));
	}
	return 0;
}