[洛谷P1062/NOIP2006普及组] 数列

首先题面是这样的：

给定一个正整数 k(3≤k≤15) ,把所有k的方幂及所有有限个互不相等的k的方幂之和构成一个递增的序列，例如，当 k=3 时，这个序列是：

1,3,4,9,10,12,13,…

因为所有的底数k都是相同的，所以自然要想到把他们的指数分离出来~~。

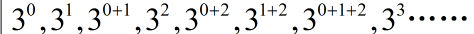例如这样

然后把指数分离出来：

0,1,0+1,2,0+2,1+2,0+1+2,3....

这时候看可能没什么头绪，但是再看一遍题目，你会发现题目中强调了两个字qwq——————— 递增。也就是说我们在确定第n项时，要从之前确定的n-1项中选出一项：

大于第n-1项但是小于目前能生成的任意一项，所以很容易想到：每确立一个数，就从数列的第一项开始逐个加上这一项，就造成了递增的效果。

但是这样做还有很大的缺陷，因为在前n-1项中，难免会有重复的项，举个最简单的例子：

0，1，0+1，2，0+2，1+2；

如果确立了第三项（0+1）的时候，对前面2项进行加法操作，明显会造成重复，并且不符合题目要求（递增和互不相等的方幂）。

那么这个算法就要进行改进。

在这里定义一下：

单独数：就是不是由加法操作得到的数（k的n次方那种qwq）

合成数：由单独数+合成数或由合成数+合成数组成的数

所以对于每一个合成数都有单独数的参与，我们想，可不可以先预处理出k的1-n次方，显然一个快速幂就可以了，那么再想想，如果每读入到一个单独数，就可以用这个单独数按照刚才的方式来得到后面的n-1项。

经过验证显然是可以的。

如样例：k=3，n=100时：

用f[i]代表第i项，有：

令v=每一个单独数f[i]

f[++i]=k(1 to n) v+f[k]

至此这个题目的分析就好了.....

下面是代码~

#include<bits/stdc++.h>
#define re register
#define ull unsigned long long
using namespace std;
int k,n,p;
ull a[1000],f[2000000];
inline int read()   //读入优化
{
    int k=1;
    int sum=0;
    char c=getchar();
    for(;'0'>c || c>'9';c=getchar())
        if(c == '-') k = -1;
    for(; '0' <= c && c <= '9'; c = getchar())
        sum = sum * 10 + c - '0';
    return sum * k;
}
inline void out(int x)       //输出优化
{
    if(x < 0) { putchar('-'); x *= -1; }
    if(x > 9) out(x / 10);
    putchar(x % 10 + '0');
}
inline ull quick_pow(int r,int k)        //快速幂
{
	ull base=r,ans=1;
	while(k!=0)
	{
		if(k&1) ans=ans*base;
		base=base*base;
		k/=2;
	}
	return ans;
}
int main()
{
	//freopen("sequence.in","r",stdin);
	//freopen("sequence.out","w",stdout);
	k=read();n=read();
	a[0]=1;a[1]=k;
	for(re int i=2;i<=n;i++) a[i]=quick_pow(k,i);        //预处理k的1-n（保险） 次幂
	for(re int i=1;i<=n;i++)
	{
		f[i]=a[p];p++; 			//对于每一个单独数的赋值
		ull tmp=f[i];			//记录v值（单独数）
		int h=i;				//确立i-1项（避免后来i的更新）
		if(i>1)
		{
			for(re int j=1;j<h;j++)
			{
				f[++i]=tmp+f[j];
				if(i>=n)
				{
					cout<<f[n];			//输出
					return 0;
				}
			}
		}
	}
	out(f[n]);
	return 0;
}