[模板] 平衡树: Splay, 非旋Treap, 替罪羊树

简介

二叉搜索树, 可以维护一个集合/序列, 同时维护节点的 \(size\), 因此可以支持 insert(v), delete(v), kth(p,k), rank(v)等操作.

另外, prev(v) == kth(rt,rank(v)-1);

next(v) == kth(rt,rank(v)+1).

平衡树通过各种方法保证二叉搜索树的平衡, 从而达到 \(O(\log n)\) 的均摊复杂度.

Splay

Splay 不仅可以实现一般平衡树的操作, 还可以实现序列的翻转/旋转等操作.

Splay 被用于LCT的操作, 保证了LCT的各种操作的复杂度也为 \(O(\log n)\).

有关 rotate

Before

After

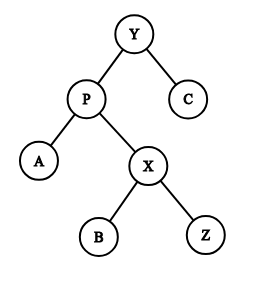
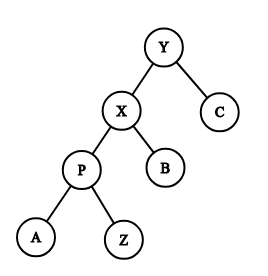
代码

以前的代码, 似乎不少地方都写麻烦了...

struct tnode{
    int val,cnt,sz,fa,son[2];
    tnode():val(0),cnt(0),sz(0),fa(0){son[0]=son[1]=0;}
    tnode(int f,int v):val(v),cnt(1),sz(1),fa(f){son[0]=son[1]=0;}
};
const int sz=100010;
struct splay{
    int rt,end;
    tnode n[sz];

    splay():rt(0),end(0) {}

    int addnode(int f,int v){
        n[++end]=tnode(f,v);
        return end;
    }

    void update(int p){
        n[p].sz=n[n[p].son[0]].sz+n[n[p].son[1]].sz+n[p].cnt;
    }

    void sf(int f,int s,int dir){
        n[f].son[dir]=s;
        n[s].fa=f;
    }
    void rotate(int p){
        int x=n[p].fa,y=n[x].fa;
        int dir=n[x].son[1]==p,dir2=n[y].son[1]==x;
        int z=n[p].son[!dir];

        sf(y,p,dir2);
        sf(x,z,dir);
        sf(p,x,!dir);

        update(x);
        update(p);
    }
    void sp(int p,int dist=0){
        if(dist==0)rt=p;
        for(int x=n[p].fa;x!=dist;x=n[p].fa){
            if(n[x].fa!=dist)
                rotate(((n[x].son[1]==p)^(n[n[x].fa].son[1]==x))?p:x);
            rotate(p);
        }
    }

    void insert(int val){
        if(rt==0){
            rt=addnode(0,val);
            return;
        }
        int now=rt;
        while(now){
            if(n[now].val==val){
                ++n[now].cnt;
                update(now);
                break;
            }
            int dir=n[now].val<val;
            if(n[now].son[dir])
                now=n[now].son[dir];
            else{
                n[now].son[dir]=addnode(now,val);
                now=n[now].son[dir];
                break;
            }
        }
        sp(now);
    }

    int min(int p){
        int fa=n[p].fa;
        while(n[p].son[0])
            p=n[p].son[0];
        sp(p,fa);
        return p;
    }

    int max(int p){
        int fa=n[p].fa;
        while(n[p].son[1])
            p=n[p].son[1];
        sp(p,fa);
        return p;
    }

    int find(int val){
        int now=rt,pr=0;
        while(now){
            pr=now;
            if(n[now].val==val)
                break;
            now=n[now].son[n[now].val<val];
        }
        sp(pr);
        return now;
    }

    int findkth(int k){
        int now=rt,pr=0;
        while(now){
            pr=now;
            int lsz=n[n[now].son[0]].sz;
            if(k>lsz&&k<=lsz+n[now].cnt)
                break;
            if(k<=lsz)
                now=n[now].son[0];
            else{
                k-=lsz+n[now].cnt;
                now=n[now].son[1];
            }
        }
        sp(pr);
        return now;
    }

    int rank(int val){
        int k=find(val);
        return k?n[n[k].son[0]].sz+1:-1;
    }

    void remove(int val){
        if(find(val)==0)return;
        if(n[rt].cnt>1){
            --n[rt].cnt;
            update(rt);
            return;
        }
        int ls=n[rt].son[0],rs=n[rt].son[1];
        if(ls==0&&rs==0){
            rt=0;
            return;
        }
        if((ls==0)^(rs==0)){
            rt=(ls!=0?ls:rs);
            n[rt].fa=0;
            return;
        }
        int newrt=min(rs);
        n[newrt].fa=0;
        n[newrt].son[0]=n[rt].son[0];
        n[n[rt].son[0]].fa=newrt;
        rt=newrt;
        update(rt);
    }

    int prev(int val){
        find(val);
        if(n[rt].val>=val)
            return max(n[rt].son[0]);
        return rt;
    }

    int next(int val){
        find(val);
        if(n[rt].val<=val)
            return min(n[rt].son[1]);
        return rt;
    }
}s;

非旋Treap

Treap 通过随机权值的堆保证树高度为 \(O(\log n)\).

Treap 可以持久化. (并不会写)

代码

struct tn{int v,p,sz,ch[2];}fhq[200060];
int rt=0,pf=0;
int newnd(int v){fhq[++pf]=(tn){v,rand(),1,{0,0}};return pf;}
void update(int p){fhq[p].sz=fhq[fhq[p].ch[0]].sz+fhq[fhq[p].ch[1]].sz+1;}

void split(int rt,int v,int &tl,int &tr){
    if(rt==0){tl=tr=0;return;}
    if(fhq[rt].v<=v)
        tl=rt,split(fhq[rt].ch[1],v,fhq[rt].ch[1],tr);
    else
        tr=rt,split(fhq[rt].ch[0],v,tl,fhq[rt].ch[0]);
    update(rt);
}
int merge(int tl,int tr){
    if(tl==0||tr==0)return tl+tr;
    if(fhq[tl].p<=fhq[tr].p){
        fhq[tl].ch[1]=merge(fhq[tl].ch[1],tr);
        update(tl);
        return tl;
    }
    else{
        fhq[tr].ch[0]=merge(tl,fhq[tr].ch[0]);
        update(tr);
        return tr;
    }
}
int kth(int &rt,int k){
    int now=rt;
    while(1){
        int tmp=fhq[fhq[now].ch[0]].sz;
        if(k<=tmp)now=fhq[now].ch[0];
        else if(k==tmp+1)return now;
        else now=fhq[now].ch[1],k-=tmp+1;
    }
}
void insert(int &rt,int v){
    int x,y;
    split(rt,v,x,y);
    rt=merge(merge(x,newnd(v)),y);
}
void remove(int &rt,int v){
    int x,y,z;
    split(rt,v,x,z);
    split(x,v-1,x,y);
    y=merge(fhq[y].ch[0],fhq[y].ch[1]);
    rt=merge(merge(x,y),z);
}
int rank(int &rt,int v){
    int x,y;
    split(rt,v-1,x,y);
    int tmp=fhq[x].sz+1;
    rt=merge(x,y);
    return tmp;
}
int prev(int &rt,int v){
    return kth(rt,rank(rt,v)-1);
}
int next(int &rt,int v){
    return kth(rt,rank(rt,v+1));
}
void print(){
    printf("dbg rt=%d\n",rt);
    printf("i  v p sz ch[0] ch[1]\n");
    rep(i,0,pf)printf("%d  %d %d %d %d %d\n",i,fhq[i].v,fhq[i].p,fhq[i].sz,fhq[i].ch[0],fhq[i].ch[1]);
    printf("dbgend\n");
}

替罪羊树

替罪羊树定义一个值 \(\alpha\), 如果左子树点数/右子树点数 > 整个子树点数\(\cdot \alpha\), 将这个子树重构.

根据势能分析, 均摊复杂度为单次操作 \(O(\log n)\) . 不会证

显然\(0.5 < \alpha < 1\), 但 \(\alpha\) 取值过大或过小都会影响代码运行效率. \(\alpha\) 可以取 \(0.7\), \(0.75\), \(0.8\) 等值, 效率没有明显差距. 这里取 \(\alpha = 0.75\).

由于替罪羊树就是有重构的二叉搜索树, 它较为容易实现, 并且常数较小.

由于替罪羊树仅仅依赖重构操作, 它还可以实现一些奇怪的操作, 比如 K-D Tree, 动态区间第k大(替罪羊树套权值线段树)等.

代码

一遍过真开心

const db alp=0.75;
//szp: number of points(includes deleted ones);
//szr: number of values(not include deleted ones; point*cnt)
struct tnd{int v,szr,szp,cnt,ch[2];}tree[nsz];
#define ls(p) tree[p].ch[0]
#define rs(p) tree[p].ch[1]
il bool isbad(int p){return tree[ls(p)].szp>tree[p].szp*alp||tree[rs(p)].szp>tree[p].szp*alp;}
il void pu(int p){
	tree[p].szp=tree[ls(p)].szp+tree[rs(p)].szp+1;
	tree[p].szr=tree[ls(p)].szr+tree[rs(p)].szr+tree[p].cnt;
}

int rt=0,pt=0,deled[nsz],pd=0;
il void init(int p,int v){tree[p]=(tnd){v,1,1,1,{0,0}};}
il int newnd(int v){
	int p=(pd?deled[pd--]:++pt);
	init(p,v);
	return p;
}

int li[nsz],pl=0;
void pia(int p){
	if(p==0)return;
	pia(ls(p));
	if(tree[p].cnt)li[++pl]=p;
	else deled[++pd]=p;
	pia(rs(p));
}
void build(int &rt,int rl,int rr){
	if(rl>rr){rt=0;return;}//important
	int mid=(rl+rr)>>1;
	rt=li[mid];
	build(ls(rt),rl,mid-1);
	build(rs(rt),mid+1,rr);
	pu(rt);
}
void rebuild(int &rt){
//	printf("RB %d\n",rt);
	pl=0;
	pia(rt);
	build(rt,1,pl);
}

void insert(int v,int &rt){
	if(rt==0){rt=newnd(v);return;}
	if(v==tree[rt].v)++tree[rt].cnt;
	else if(v<tree[rt].v)insert(v,ls(rt));
	else insert(v,rs(rt));
	pu(rt);
	if(isbad(rt))rebuild(rt);
}
void remove(int v,int rt){
	if(rt==0)return;
	if(v==tree[rt].v){if(tree[rt].cnt)--tree[rt].cnt;}
	else if(v<tree[rt].v)remove(v,ls(rt));
	else remove(v,rs(rt));
	pu(rt);
}

int rk(int v,int rt){
	int ans=1;
	while(rt){
		if(v==tree[rt].v){ans+=tree[ls(rt)].szr;break;}
		else if(v<tree[rt].v)rt=ls(rt);
		else ans+=tree[ls(rt)].szr+tree[rt].cnt,rt=rs(rt);
	}
	return ans;
}
int kth(int k,int rt){
	int fl=0;
	while(rt){
		if(k<=tree[ls(rt)].szr)rt=ls(rt),fl=0;
		else{
			k-=tree[ls(rt)].szr;
			if(k<=tree[rt].cnt)return tree[rt].v;
			else k-=tree[rt].cnt,rt=rs(rt),fl=1;
		}
	}
	return fl?1e8:-1e8;
}

int prev(int v){return kth(rk(v,rt)-1,rt);}
int next(int v){return kth(rk(v+1,rt),rt);}

用于测试的输入/输出

由于某谷样例较弱, 窝就造了一个...

// it also tests rebuild() func in Scapegoat Tree
// and invalid input (output -inf/inf in my code)
// sample input
21
1 5
1 4
1 5
2 4
1 3
1 2
1 1
1 0
4 3
3 4
3 6
1 15
1 14
1 13
1 12
1 11
5 5
6 5
5 0
6 15
4 20

// sample output
2
5
7
3
11
-100000000
100000000
100000000

// output with "RB" (aka rebuild())
i=1
i=2
i=3
i=4
i=5
i=6
i=7
RB 1
i=8
i=9
2
i=10
5
i=11
7
i=12
i=13
i=14
RB 3
i=15
i=16
i=17
3
i=18
11
i=19
-100000000
i=20
100000000
i=21
100000000