Manacher算法详解

问题

什么是回文串，如果一个字符串正着度读和反着读是一样的，这个字符串就被称为回文串。

such as

noon level aaa bbb

既然有了回文，那就要有关于回文的问题，于是就有了——

最长回文子串：给定一个字符串，求它的最长回文子串长度。

暴力

找出所有的子串，遍历每个子串判断他们是否为回文串。

时间复杂度\(O(n^3)\)

优化

因为回文串是对称的，根据这个性质，枚举每个位置，找在这个位置上能扩展到的最长回文串。

时间复杂度\(O(n^2)\)

Manacher算法

打开洛谷的模板题发现数据范围是\(10^7\)，还是不能过，怎么办。

先分析优化后的暴力的不足。

1.对于长度为奇数的回文和长度为偶数的回文，它们的对称轴是不一样的，要分类讨论。

2.有些子串会被访问多次。

比如 :

char: a b a b a b a ...
　i : 0 1 2 3 4 5 6 ...

我们枚举到第\(i\)位：

\(i==3\)时第一个"aba"被遍历了一次；

\(i==4\)时第一个"aba"又被遍历了一次；

\(i==5\)时第一个"aba"双被遍历了一次；

.......……

\(i==len/2\)时第一个"aba"又双叒叕被遍历了一次。

处理字符串长度的奇偶性带来的对称轴不确定问题

如果字符串的长度都是奇数就好办了。

处理原来的字符串，在收尾和所有空隙插入一个相同的无关的字符，插入后原字符串中是回文的子串还是回文串，不是回文的子串的依然不是。

但字符串的长度都变成了\(2*len+1\)，都成了奇数.

为什么是\(2*len+1\)，因为有\(len-1\)个空，两边又分别插入了\(2\)个，加起来等于\(len+(len-1)+2=2*len+1\)。

如：

长度为奇数的字符串

ababa　---> @#a#b#a#b#a#

长度为偶数的字符串

1221　---> @#1#2#2#1#

'@'用来防止数组越界

找最长回文串

回文半径：把一个回文串中最左或最右位置的字符到其对称轴的距离称为回文半径

在Manacher算法中，我们用\(p[i]\)表示第\(i\)个字符的回文半径

    char : # a # b # c # b # a #
    p[i] : 1 2 1 2 1 6 1 2 1 2 1
p[i] - 1 : 0 1 0 1 0 5 0 1 0 1 0
       i : 1 2 3 4 5 6 7 8 9 10 11

显然，最大的\(p[i]-1\)就是答案

显然这个结论非常不显然，单从数值上看的话，插入完字符之后对于一个回文串的长度为原串长度*2+1，等于这个回文串回文半径*2+1，显然相等。

这样我们的问题就转换成了怎样快速的求出\(p\)数组

在这里我们利用回文串的对称性扩展回文串，p[i]不再直接赋值为1，而是根据之前求出的p[j]，0<j<i。

我们用\(mx\)表示所有字符产生的最大回文子串的最大右边界，\(id\)表示产生这个最大右边界的对称轴的位置。

为什么要维护这些东西，因为我们要利用回文串的对称性来更新当前位置的值，维护了右边界(mx)后就可以直接判断当前位置是否可以直接利用对称性来更新（因为之前找到的回文串最右端就是到\(mx\)，超出\(mx\)的话就不能利用对称性来更新了）；\(id\)是对称轴，用来求关于\(i\)对称的位置\(j\)。

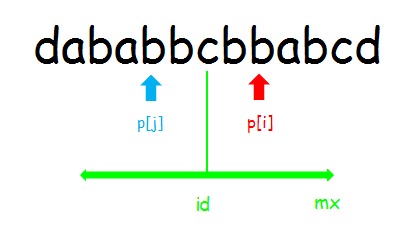
中间的#懒得画了就

如图，假设我们已经求出了\(p[1...7]\)，当\(i<mx\)时，因为\(id\)被更新过了，而\(i\)是\(id\)之后的位置，第\(i\)个字符一定落在\(id\)的右边。这时我们关心的还是\(i\)是在\(mx\)的左边还是右边。

以下内容为了方便我们定义：

串\(i\)表示以\(i\)为对称轴的回文串(用红色的箭头表示)；

串\(j\)表示以\(j\)为对称轴的回文串(用蓝色的箭头表示)；

串\(id\)表示以\(id\)为对称轴的回文串(用绿色的箭头表示)；

情况1：i < mx

如上图，利用回文串的性质，对于\(i\)，我们可以找到一个关于\(id\)对称的位置\(j=id*2-i\)，进行加速查找

但在这里又细分为了三种情况

(1)



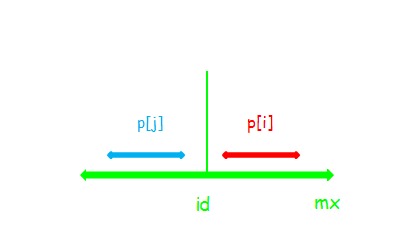
显然此时\(p[i]=p[j]\)。

对于这种情况，串\(i\)不可以再向两边扩张。

如果可以向两边扩张的话，\(p[j]\)也可以再向两边扩张，而\(p[j]\)已经确定了，所以串\(i\)不向两边扩张。

(2)



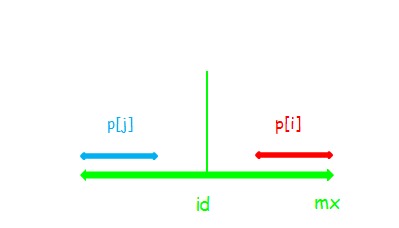
显然此时\(p[i]=p[j]\)

与(1)不同的是，串\(i\)是可以再向两边扩张的。

应该很显然，一比划就知道。

(3)



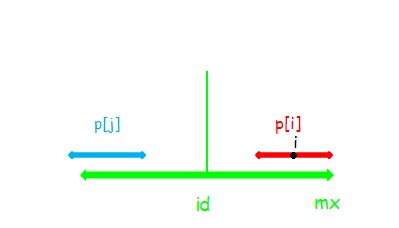
此时\(p[i]=mx-i\)

这时我们只能确定串\(i\)在\(mx\)以内的部分是回文的，并不能确定串\(i\)和串\(j\)相同。

同样，这时我们的串\(i\)是不可以再向两端扩张的。



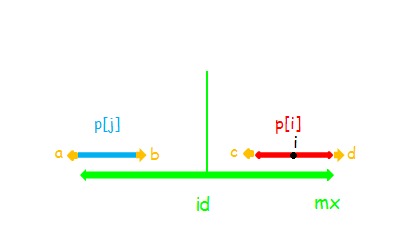
如果串\(i\)可以扩张，如图，则\(d=c\)，根据对称性\(c=b\)，又因为\(a=b\)，所以\(a=d\)，可以看到，串\(id\)可以继续扩张，因为\(p[id]\)已经固定了，所以串\(i\)不可以继续扩张

情况2：i >= mx

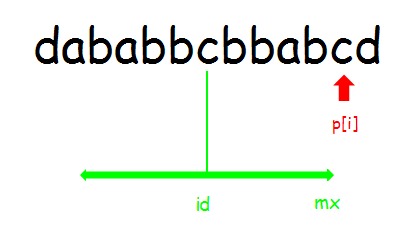
这时之前记录的信息都用不上了，于是\(p[i]=1\)。

综上所述

    if (i < mx) p[i] = min(p[id * 2 - i], mx - i);   //情况1
    else p[i] = 1;    //情况2
    while (str[i + p[i]] == str[i - p[i]]) p[i]++;    //暴力扩展
	if (p[i] + i > mx) mx = p[i] + i, id = i;    //更新id位置
}

代码

P3805 【模板】manacher算法

#include <bits/stdc++.h>
using namespace std;
const int N = 22000010;
char s[N];
char str[N];
int p[N];
int init() {
    int len = strlen(s);
    str[0] = '@', str[1] = '#';
    int j = 2;
    for (int i = 0; i < len; ++i) str[j++] = s[i], str[j++] = '#';
    str[j] = '\0';
    return j;
}
int manacher() {
    int ans = -1, len = init(), mx = 0, id = 0;
    for (int i = 1; i < len; ++i) {
        if (i < mx) p[i] = min(p[id * 2 - i], mx - i);
        else p[i] = 1;
        while (str[i + p[i]] == str[i - p[i]]) p[i]++;
        if (p[i] + i > mx) mx = p[i] + i, id = i;
        ans = max(ans, p[i] - 1);
    }
    return ans;
}

int main() {
    cin >> s;
    cout << manacher();
    return 0;
}