剑指offer 4.树 重建二叉树

题目描述

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

 

解题思路

已知二叉树的前序遍历和中序遍历：
PreOrder:         GDAFEMHZ
InOrder:            ADEFGHMZ
我们如何还原这颗二叉树，并求出他的后序遍历？

我们基于一个事实：中序遍历一定是 { 左子树中的节点集合 }，root，{ 右子树中的节点集合 }，前序遍历的作用就是找到每颗子树的root位置。

算法1
输入：前序遍历，中序遍历
1、寻找树的root，前序遍历的第一节点G就是root。
2、观察前序遍历GDAFEMHZ，知道了G是root，剩下的节点必然在root的左或右子树中的节点。
3、观察中序遍历ADEFGHMZ。其中root节点G左侧的ADEF必然是root的左子树中的节点，G右侧的HMZ必然是root的右子树中的节点，root不在中序遍历的末尾或开始就说明根节点的两颗子树都不为空。
4、观察左子树ADEF，按照前序遍历的顺序来排序为DAFE，因此左子树的根节点为D，并且A是左子树的左子树中的节点，EF是左子树的右子树中的节点。
5、同样的道理，观察右子树节点HMZ，前序为MHZ，因此右子树的根节点为M，左子节点H，右子节点Z。

观察发现，上面的过程是递归的。先找到当前树的根节点，然后划分为左子树，右子树，然后进入左子树重复上面的过程，然后进入右子树重复上面的过程。最后就可以还原一棵树了：

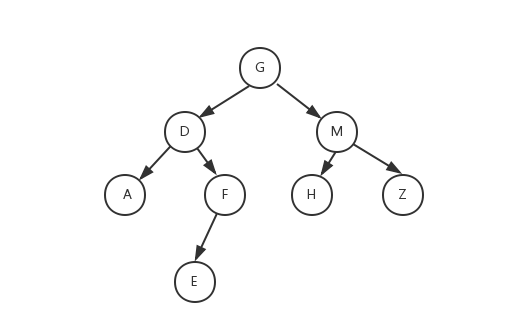
从而得到PostOrder:       AEFDHZMG
改进：
更进一步说，其实，如果仅仅要求写后续遍历，甚至不要专门占用空间保存还原后的树。只需要用一个数组保存将要得到的后序，就能实现：

具体思路如下：

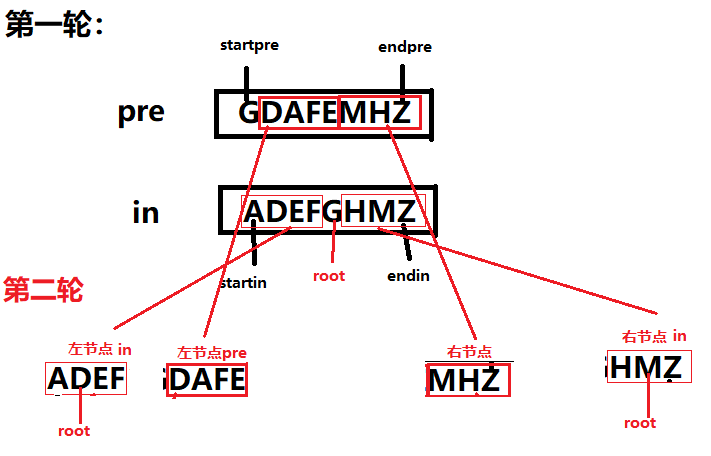
左节点:

---

startpre=startPre+1,

startend=startPre+i-startIn

startin=startIn,

endin=i-1

---

右节点：

---

startpre=i-startIn+startPre+1,

startend=endPre

startin=i+1,

endin=endIn

---

具体实现代码如下：

public class ReConstructBinaryTree {

//Definition for binary tree
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}

public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
TreeNode rootofpre=new TreeNode(pre[0]);
return reConstructBinaryTree(pre,0,pre.length-1,in,0,in.length-1);

}

//前序遍历{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}
private TreeNode reConstructBinaryTree(int [] pre,int startPre,int endPre,int [] in,int startIn,int endIn) {
if (startPre>endPre||startIn>endIn) {
return null;
}
TreeNode root=new TreeNode(pre[startPre]);
for (int i = 0; i < in.length; i++) {
if (root.val==in[i]) {
root.left=reConstructBinaryTree(pre, startPre+1, startPre+i-startIn, in, startIn, i-1);
root.right=reConstructBinaryTree(pre,i-startIn+startPre+1,endPre,in,i+1,endIn);
break;

}
}

return root;

}
}
}