方便快捷的求导求积分解方程在线工具sage介绍

  有时候我们需要进行一些复杂的数学计算，比如求导， 求积分，解方程，还是用abcd字母代表变量的方程等，这就需要进行复杂的数学运算还需要具备良好的数学基础。不过现在有一个非常方便的在线工具，只需要几秒钟， 就能告诉我们所有的答案。

sage

 &ems;sage是一个免费开源的数学计算软件系统， 里面包含了许多的package，比如NumPy, SciPy, matplotlib， Sympy, Maxima, GAP， FLINT, R 等。默认情况下，既可以运行sage自身的语法， 也兼容python的语法。正因为内部整合了许多包，所以它的安装包非常大，当然，它也有在线版本SageMathCell实现方便的在线运算。SageMathCell:http://sagecell.sagemath.org/

sage介绍

输入框是代码框，点evaluate之后，会在下面出现结果框（计算的结果或者是画的图形）， 并且在代码框右下方有一个切换语言的选项。代码框支持tab补全，支持？ + 函数来查看函数帮助。

进行基本的运算

求导

x = var(x) #声明x为变量
f(x) = x^3 + x^2 +2 #定义函数f(x)
diff(f, x)  #f(x) 对x 求导

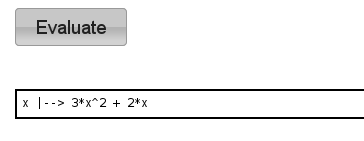
不定积分

integral(f, x)  # f(x) 对x不定积分

定积分

integral(f, x, 0, 1)  #f(x) 对x 0,1 定积分

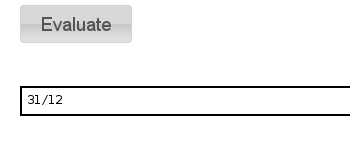
解方程

var('x y p q') #声明变量
eq1 = p+q==9  #等式1
eq2 = q*y+p*x==-6  #等式2
eq3 = q*y^2+p*x^2==24  #等式3
solve([eq1, eq2, eq3,p==1],p,q,x,y) #已知 p==1解方程

[[p == 1, q == 8, x == -4/3*sqrt(10) - 2/3, y == 1/6*sqrt(10) - 2/3], [p == 1, q == 8, x == 4/3*sqrt(10) - 2/3, y == -1/6*sqrt(10) - 2/3]]

泰勒展开

var('x a')
f(x) = sqrt(x+a)
taylor(f,x, 1, 2) #f(x)在1处水平为2进行泰勒展开

绘图

circle((0,0), 1, rgbcolor=(1,1,0)) #圆心为0，0半径为1的圆

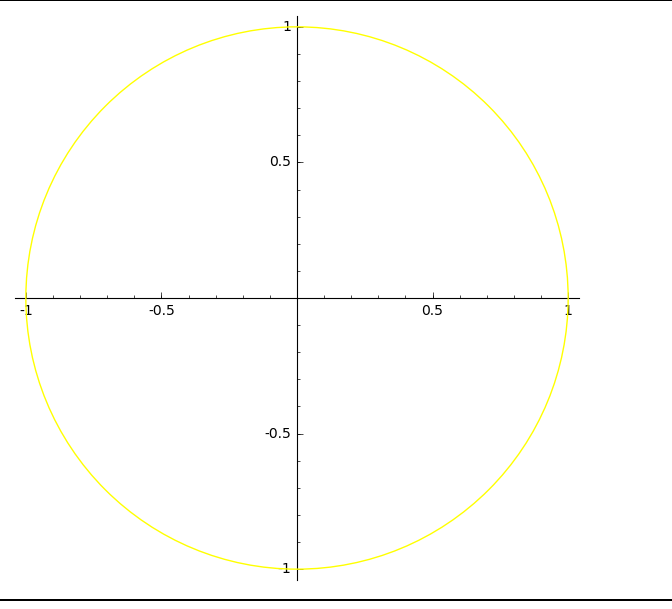
以上只是作为基本的引入， 更多的内容可以自己去看manual，它具有几乎所有你能想象的到的非常强大的数学计算功能。

参考资料

Sage tutorial: http://doc.sagemath.org/html/en/tutorial/index.html

Philipp K. Janert, Data Analysis with Open Source Tools