BZOJ.4144.[AMPPZ2014]Petrol(Kruskal重构树)

BZOJ

看别人代码的时候发现哪一步都很眼熟，突然想起来，就在四个月前我好像看过还给别人讲过？mmp=v=

果然不写写就是容易忘。写了好歹忘了的时候还能复习呢（虽然和看别人的好像也没多少差别？）。

---

首先非加油站的点是没有用的。考虑如何删掉这些点然后在加油站之间连对应的边。

搬这里的一张图：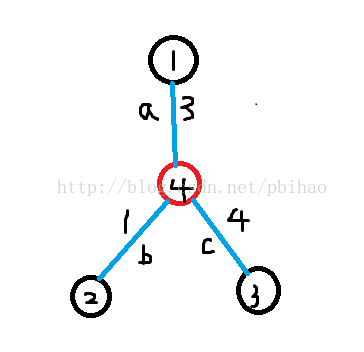

因为\(b<a\ \&\&\ b<c\)，所以有\(b+c<a+c\ \&\&\ b+a<a+c\)，也就是到一个点时，先去一次离它最近的点加油再去其它的点一定不会更差。记\(bel[p]\)为离\(p\)点最近的加油站，\(dis[p]\)为\(bel[p]\)到\(p\)的距离，对于一条边\((u,v,w)\)，若\(bel[u]\neq bel[v]\)，那么就在\(bel[u],bel[v]\)之间加一条\(dis[u]+dis[v]+w\)的边即可。（因为从任何一个点出发到了\(u\)，先去一次\(bel[u]\)再去别的点不会更差，所以直接和\(bel[u]\)连边就行了）

具体就是以所有加油点为起点，\(Dijkstra\)跑一遍多源最短路。

然后求一遍最小生成树。询问就判断两点间路径上的最大值即可。

注意求生成树的时候可以直接按秩合并将树高保持在\(O(\log n)\)的高度。对于询问暴力跳\(fa\)即可。

要注意图可能不连通！！

---

//20216kb	2600ms
#include <queue>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#define mp std::make_pair
#define pr std::pair<int,int>
#define gc() getchar()
#define MAXIN 500000
//#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
typedef long long LL;
const int N=2e5+5;
int Enum,H[N],nxt[N<<1],to[N<<1],len[N<<1],dis[N],bel[N],F[N],fa[N],w[N],rk[N],dep[N];
char IN[MAXIN],*SS=IN,*TT=IN;
std::priority_queue<pr> q;
struct Edge
{
	int u,v,w;
	bool operator <(const Edge &x)const
	{
		return w<x.w;
	}
}e[N<<1];//双向边啊 
inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-48,c=gc());
	return now;
}
inline void AE(int w,int v,int u)
{
	to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum, len[Enum]=w;
	to[++Enum]=u, nxt[Enum]=H[v], H[v]=Enum, len[Enum]=w;
}
int Dijkstra()
{
	static bool vis[N];
	int cnt=0;
	while(!q.empty())
	{
		int x=q.top().second; q.pop();
		if(vis[x]) continue;
		vis[x]=1;
		for(int i=H[x],v; i; i=nxt[i])
			if(dis[v=to[i]]>dis[x]+len[i])
				dis[v]=dis[x]+len[i], bel[v]=bel[x], q.push(mp(-dis[v],v));
			else if(bel[x]!=bel[v])
				e[++cnt]=(Edge){bel[x],bel[v],dis[x]+dis[v]+len[i]};
	}
	return cnt;
}
int Find(int x)
{
	return x==F[x]?x:F[x]=Find(F[x]);
}
void GetDep(int x)
{
	if(fa[x]&&!dep[fa[x]]) GetDep(fa[x]);
	dep[x]=dep[fa[x]]+1;
}
void Kruskal(const int n,const int m)
{
	std::sort(e+1,e+1+m);
	for(int i=1; i<=n; ++i) F[i]=i;
	for(int i=1,r1,r2,k=1; i<=m; ++i)
	{
		if((r1=Find(e[i].u))==(r2=Find(e[i].v))) continue;
		if(rk[r1]<rk[r2]) std::swap(r1,r2);//r2->r1
		else if(rk[r1]==rk[r2]) ++rk[r1];
		F[r2]=r1, fa[r2]=r1, w[r2]=e[i].w;
	}
	for(int i=1; i<=n; ++i) if(!dep[i]) GetDep(i);
}
inline bool Query()
{
	int u=read(),v=read(),val=read();
	if(Find(u)!=Find(v)) return 0;//!
	if(dep[u]<dep[v]) std::swap(u,v);
	for(int tmp=dep[v]; dep[u]>tmp; u=fa[u])
		if(w[u]>val) return 0;
	for(; u!=v; u=fa[u],v=fa[v])
		if(w[u]>val||w[v]>val) return 0;
	return 1;
}
int main()
{
	const int n=read(),s=read(),m=read();
	memset(dis,0x7f,sizeof dis);
	for(int i=1,x; i<=s; ++i) dis[x=read()]=0, bel[x]=x, q.push(mp(0,x));
	for(int i=1; i<=m; ++i) AE(read(),read(),read());
	int cnt=Dijkstra(); Kruskal(n,cnt);
	for(int Q=read(); Q--; puts(Query()?"TAK":"NIE"));
	return 0;
}