PCA学习笔记

主成分分析（Principal Component Analysis，简称PCA）是最常用过的一种降维方法

在引入PCA之前先提到了如何使用一个超平面对所有的样本进行恰当的表达?

即若存在这样的超平面，那么它大概应具有这样的性质：

• • 最大可分性：样本点在这个超平面的投影尽可能分开。
  • 最近重构性：样本点到这个超平面的距离都足够近。

从最大可分性出发，能得到主成分分析的另一种解释。样本点Χ_i在新空间中超平面上的投影是W^TX_i ，若所有样本点的投影尽可能分开，则应该使投影后样本点的方差最大化。投影后的样本点的方差是∑_i WTx_ix_i^TW，于是优化目标可写为：

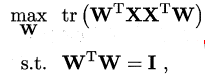
基于最近重构行推导出的最终的结果和上面的目标等价，可以使用拉格朗日乘子法求解上面的优化问题，得到：

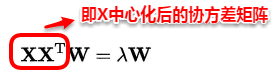
因此，只需对协方差矩阵进行特征分解即可求接触W，PCA学习算法的整个流程如下：

问题：为什么最大的d'个特征值多对应的特征向量的投影矩阵W*可以保留最大的信息？（降维后要最大化保留数据内在的信息，并期望在所投影的维度上的离散度最大）

 简单来说：主成分分析就是找出数据里最主要的方面，用数据里最主要的方面来代替原始数据