32-1题：不分行从上到下打印二叉树/BFS/deque/queue

题目

从上往下打印出二叉树的每个节点，同层节点从左至右打印。

---

考点

1.广度优先遍历

2.binary tree

3.queue

4.deque

---

思路

按层打印：8、6、10、5、7、9、11

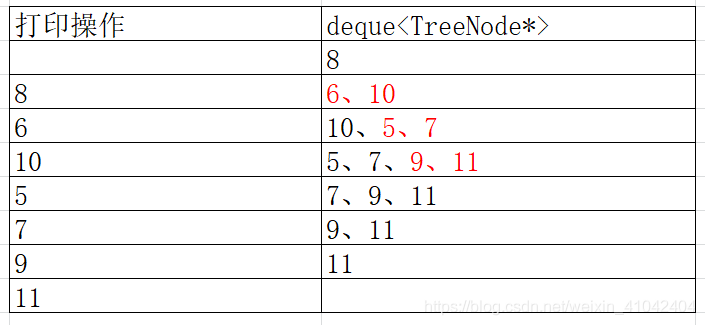
用STL的deque完成两端进出的操作。

规律：

1.从头节点开始放入容器。

2.每次打印一个节点时，如果该节点有子节点，将其左子节点、右子节点依次放入容器内。

3.接下来打印deque的front().直到deque里面没有值。

---

代码

newcoder

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    vector<int> PrintFromTopToBottom(TreeNode* root) {
        //1.定义返回值
        vector<int> result;
         //2.入口鲁棒性测试
        if(!root)
            return result;

        //3.定义节点队列
        deque<TreeNode*> dequeTree;

        //4.将头节点入deque
        dequeTree.push_back(root); 

        //5.打印剩下容器的节点
        while( !dequeTree.empty())
        {
            TreeNode* cur=dequeTree.front();
            result.push_back(cur->val);
            dequeTree.pop_front();

            if(cur->left)
                dequeTree.push_back(cur->left);

            if(cur->right)
                dequeTree.push_back(cur->right);
        }

        //6.返回结果
        return result;
    }
};

---

问题

1.数组越界

访问树的子节点操作时，一定要判断子节点是否存在。

---

2.deque

Iterators:

begin

end

rbegin

Return reverse iterator to reverse beginning (public member function )

rend

Return reverse iterator to reverse end (public member function )

cbegin 

Return const_iterator to beginning (public member function )

cend 

Return const_iterator to end (public member function )

crbegin 

Return const_reverse_iterator to reverse beginning (public member function )

crend 

Return const_reverse_iterator to reverse end (public member function )

Capacity:

size

max_size

resize

Change size (public member function )

empty

shrink_to_fit 

Shrink to fit (public member function )

Element access:

operator[]

at

Access element (public member function )

front

back

Modifiers:

assign

Assign container content (public member function )

push_back

push_front

pop_back

pop_front

insert

Insert elements (public member function )

erase

Erase elements (public member function )

swap

Swap content (public member function )

clear

emplace 

Construct and insert element (public member function )

emplace_front 

Construct and insert element at beginning (public member function )

emplace_back 

Construct and insert element at the end (public member function )

3.广度优先遍历

广度优先遍历有向图，也可以基于队列实现，树是图的特殊退化形式，从上至下遍历二叉树本质上就是广度优先遍历二叉树。

BFS不管遍历有向图还是树，都要用队列，首先把起始节点(根节点）放入队列，接下来每次取出头部的一个节点，遍历这个节点之后，把他能达到的节点（子节点）全部放入队列的尾部。重复这个过程，直到队列中所有节点遍历完成。