poj3233(矩阵快速幂的和)

题目链接：http://poj.org/problem?id=3233

Matrix Power Series

Time Limit: 3000MS		Memory Limit: 131072K
Total Submissions: 28105		Accepted: 11461

Description

Given a n × n matrix A and a positive integer k, find the sum S = A + A² + A³ + … + A^k.

Input

The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 10⁹) and m (m < 10⁴). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.

Output

Output the elements of S modulo m in the same way as A is given.

Sample Input

2 2 4
0 1
1 1

Sample Output

1 2

   2 3

思路：之前做的都是直接求矩阵的多少次方，这次做的是不仅仅要求多少次方，还要求它们的和，那么该怎么做呢？  刚开始想的是会不会是用一个for循环把1~k每一个都用一次矩阵快速幂，但是很快就否认了，这样肯定会超时，
然后想了很久，发现其实是这样的：
这题就是求一个矩阵的和式:S(k),直接对和式建立递推：

建立矩阵,注意此处S和A都是2*2的矩阵，E表示单位矩阵,O表示零矩阵(全是0,与其他矩阵相乘都为0),显然E,O都是2*2的

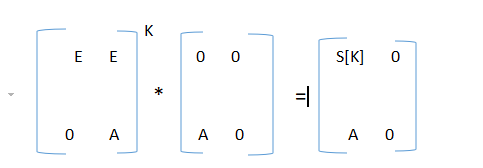
所以第一个样例是一个4*4的矩阵，

所以每次我们构造矩阵都是构造n*2的矩阵

具体看代码：

#include<iostream>
#include<string.h>
#include<map>
#include<cstdio>
#include<cstring>
#include<stdio.h>
#include<cmath>
#include<ctype.h>
#include<math.h>
#include<algorithm>
#include<set>
#include<queue>
typedef long long ll;
using namespace std;
const ll mod=;
const int maxn=+;
const int maxk=5e3+;
const int maxx=1e4+;
const ll maxe=+;
#define INF 0x3f3f3f3f3f3f
#define Lson l,mid,rt<<1
#define Rson mid+1,r,rt<<1|1
struct matrix
{
    int a[maxn<<][maxn<<];
}ans,res,c;
int n,k,m;
int b[maxn<<][maxn<<];
void init()//这里全都是给矩阵赋值的过程
{
    memset(ans.a,,sizeof(ans.a));
    memset(res.a,,sizeof(res.a));
    memset(c.a,,sizeof(c.a));
    for(int i=;i<n;i++)
    {
        for(int j=;j<n;j++)
            cin>>b[i][j];//输入的矩阵
    }
    for(int i=n;i<n*;i++)
    {
        for(int j=;j<n;j++)
        {
            c.a[i][j]=b[i-n][j];//代表第二个矩阵，也就是不变的那个
        }

    }
    for(int i=;i<n;i++)
    {
        res.a[i][i]=res.a[i][i+n]=;//单位矩阵的赋值
    }
    for(int i=n;i<n*;i++)
    {
        for(int j=n;j<n*;j++)
        {
            res.a[i][j]=b[i-n][j-n];//转移矩阵
        }
    }
    for(int i=;i<n*;i++)
        ans.a[i][i]=;//单位矩阵
}
matrix multiply(matrix x,matrix y)
{
    matrix temp;
    memset(temp.a,,sizeof(temp));
    for(int i=;i<n*;i++)
    {
        for(int j=;j<n*;j++)
        {
            for(int l=;l<n*;l++)
            {
                temp.a[i][j]=(temp.a[i][j]+x.a[i][l]*y.a[l][j]%m)%m;
            }
        }
    }
    return temp;
}
void Quickpow()//这里每个矩阵快速幂都是一样的
{
    while(k)
    {
        if(k&)
            ans=multiply(ans,res);
        res=multiply(res,res);
        k>>=;
    }
}
void solve()//这就是最后两个矩阵相乘的过程了
{
    ans=multiply(ans,c);
    for(int i=;i<n;i++)
    {
        for(int j=;j<n;j++)
            cout<<ans.a[i][j]<<" ";//最后只要输出左上角那个矩阵就好了
        cout<<endl;
    }
}
int main()
{
    cin>>n>>k>>m;
    init();
    Quickpow();
    solve();
    return ;
}