CF959E Mahmoud and Ehab and the xor-MST 思维

Ehab is interested in the bitwise-xor operation and the special graphs. Mahmoud gave him a problem that combines both. He has a complete graph consisting of n vertices numbered from 0 to n - 1. For all 0 ≤ u < v < n, vertex u and vertex v are connected with an undirected edge that has weight (where is the bitwise-xor operation). Can you find the weight of the minimum spanning tree of that graph?

You can read about complete graphs in https://en.wikipedia.org/wiki/Complete_graph

You can read about the minimum spanning tree in https://en.wikipedia.org/wiki/Minimum_spanning_tree

The weight of the minimum spanning tree is the sum of the weights on the edges included in it.

Input

The only line contains an integer n (2 ≤ n ≤ 10¹²), the number of vertices in the graph.

Output

The only line contains an integer x, the weight of the graph's minimum spanning tree.

Example

Input

Copy

4

Output

Copy

4

Note

In the first sample: 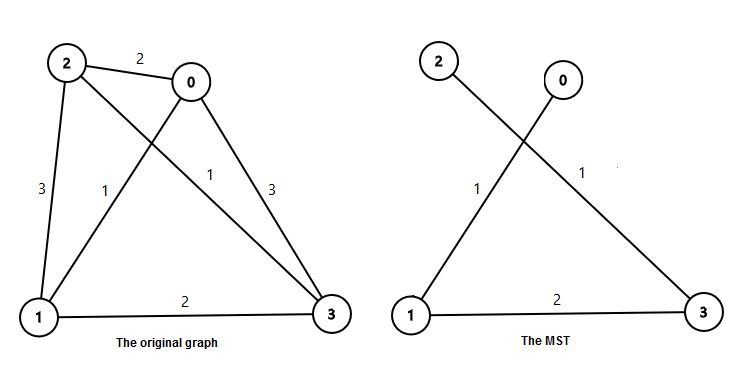The weight of the minimum spanning tree is 1+2+1=4.

题意翻译

n个点的完全图标号(0-n-1),i和j连边权值为i^j,求MST的值

不妨先手算几项，可以发现每一位上的贡献为当前n 的一半；

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 300005
#define inf 0x3f3f3f3f
#define INF 9999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
//const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)

inline ll rd() {
	ll x = 0;
	char c = getchar();
	bool f = false;
	while (!isdigit(c)) {
		if (c == '-') f = true;
		c = getchar();
	}
	while (isdigit(c)) {
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	return f ? -x : x;
}

ll gcd(ll a, ll b) {
	return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }

/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
	if (!b) {
		x = 1; y = 0; return a;
	}
	ans = exgcd(b, a%b, x, y);
	ll t = x; x = y; y = t - a / b * y;
	return ans;
}
*/

ll qpow(ll a, ll b, ll c) {
	ll ans = 1;
	a = a % c;
	while (b) {
		if (b % 2)ans = ans * a%c;
		b /= 2; a = a * a%c;
	}
	return ans;
}

int main()
{
	//ios::sync_with_stdio(0);
	ll n; rdllt(n);
	ll ans = 0;
	ll tmp = 1;
	while (n>1) {
		ans += tmp * (n >> 1); tmp <<= 1; n -= (n >> 1);
	//	cout << n<<' '<<ans << endl;
	}
	cout << ans << endl;
    return 0;
}