第99:真正理解拉格朗日乘子法和 KKT 条件

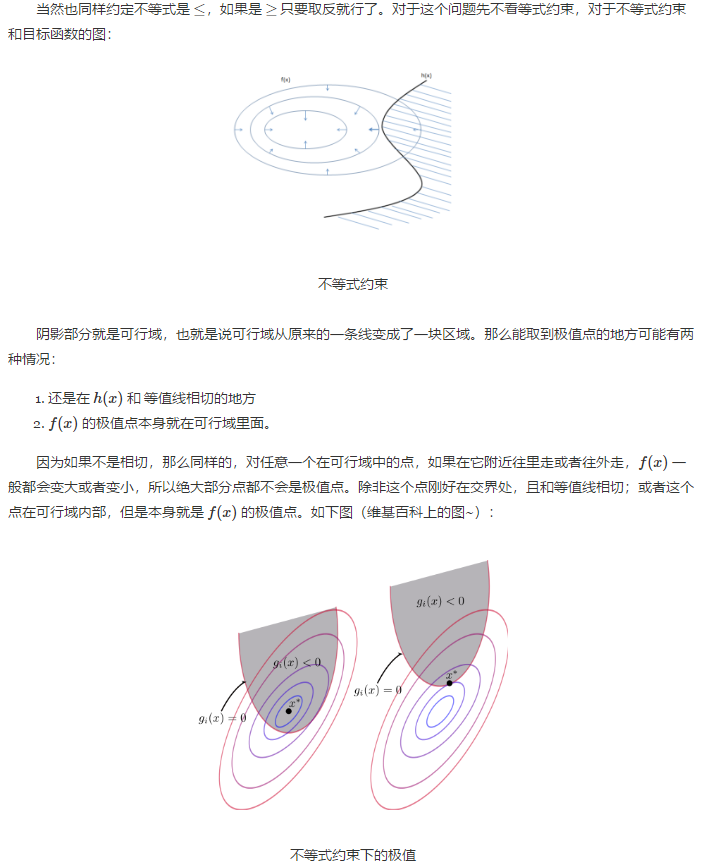



第99:真正理解拉格朗日乘子法和 KKT 条件的更多相关文章
- 真正理解拉格朗日乘子法和 KKT 条件
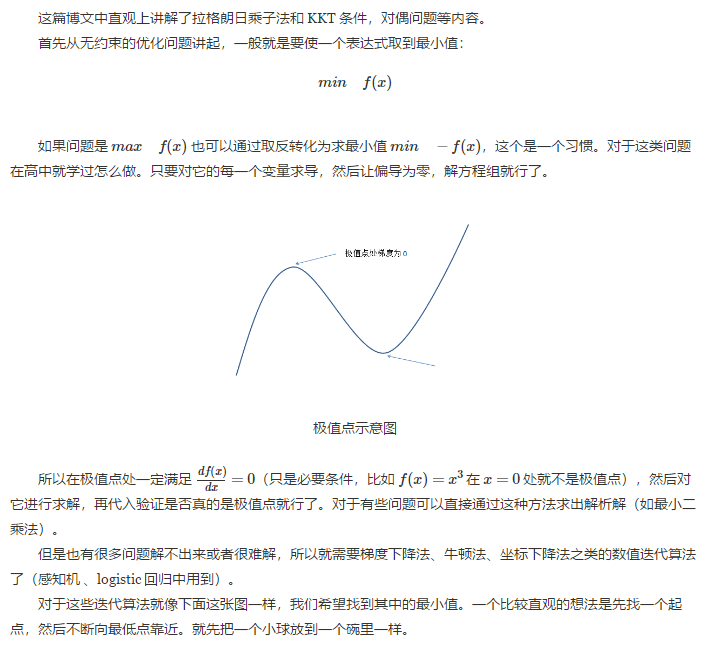
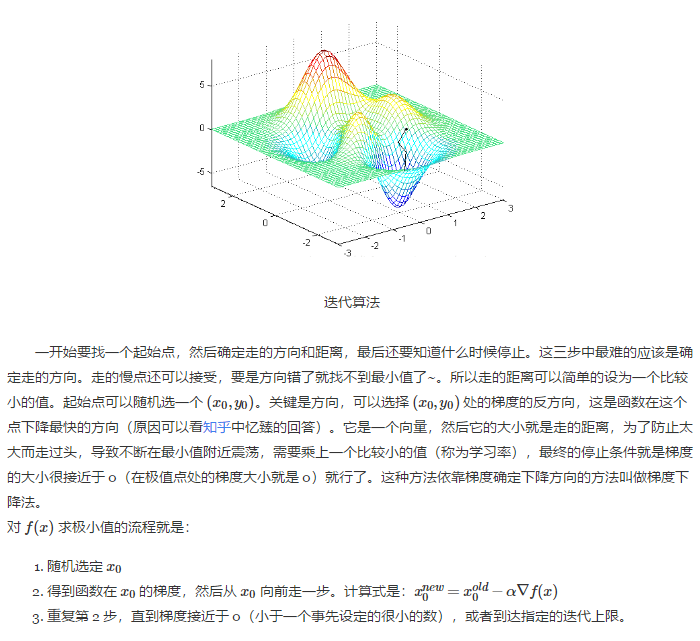
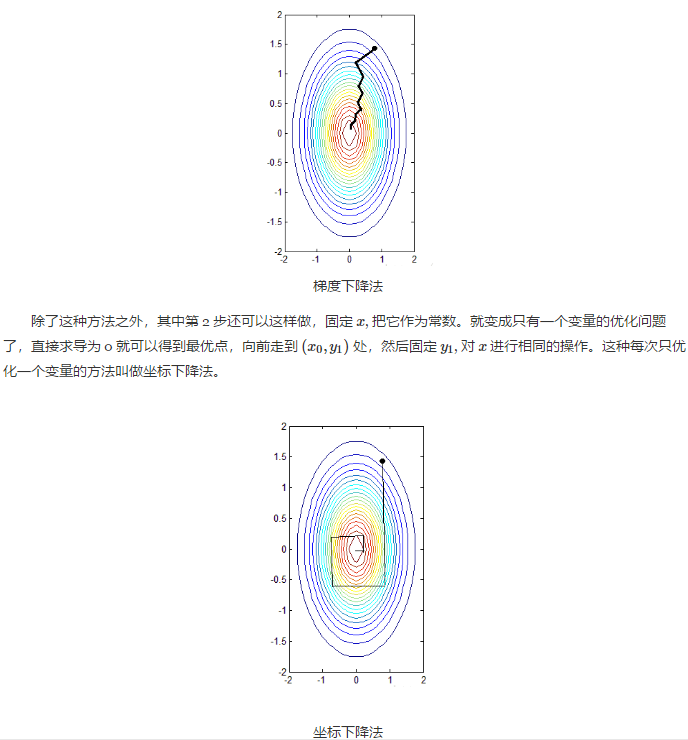
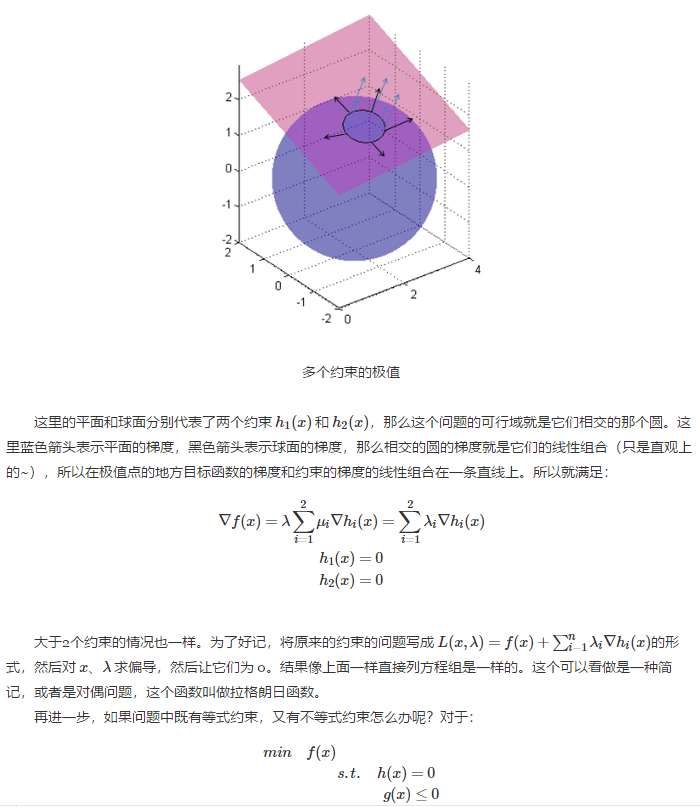
这篇博文中直观上讲解了拉格朗日乘子法和 KKT 条件,对偶问题等内容. 首先从无约束的优化问题讲起,一般就是要使一个表达式取到最小值: \[min \quad f(x)\] 如 ...
- 关于拉格朗日乘子法和KKT条件
解密SVM系列(一):关于拉格朗日乘子法和KKT条件 标签: svm算法支持向量机 2015-08-17 18:53 1214人阅读 评论(0) 收藏 举报 分类: 模式识别&机器学习(42 ...
- 机器学习笔记——拉格朗日乘子法和KKT条件
拉格朗日乘子法是一种寻找多元函数在一组约束下的极值方法,通过引入拉格朗日乘子,可将有m个变量和n个约束条件的最优化问题转化为具有m+n个变量的无约束优化问题.在介绍拉格朗日乘子法之前,先简要的介绍一些 ...
- 重温拉格朗日乘子法和KKT条件
在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法,对于等式约束的优化问题,可以应用拉格朗日乘子法去求取最优值:如果含有不等式 ...
- 拉格朗日乘子法和KKT条件
拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush-Kuhn-Tucker)条件是求解约束优化问题的重要方法,在有等式约束时使用拉格朗日乘子法,在有不等约束时使用KKT条件 ...
- 拉格朗日乘子法 - KKT条件 - 对偶问题
接下来准备写支持向量机,然而支持向量机和其他算法相比牵涉较多的数学知识,其中首当其冲的就是标题中的拉格朗日乘子法.KKT条件和对偶问题,所以本篇先作个铺垫. 大部分机器学习算法最后都可归结为最优化问题 ...
- 拉格朗日乘子法&KKT条件
朗日乘子法(Lagrange Multiplier)和KKT(Karush-Kuhn-Tucker)条件是求解约束优化问题的重要方法,在有等式约束时使用拉格朗日乘子法,在有不等约束时使用KKT条件.前 ...
- 【整理】深入理解拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
在求解最优化问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法.在有等式约束时使用拉格朗日乘子法,在有不等约束时使用 ...
- 深入理解拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
[整理] 在求解最优化问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法.在有等式约束时使用拉格朗日乘子法,在有 ...
随机推荐
- js手写笔记
1.document.write(); 2.document.getElementById("").style.color="red";//sytle.font ...
- LeetCode 24. 两两交换链表中的节点(Swap Nodes in Pairs)
题目描述 给定一个链表,两两交换其中相邻的节点,并返回交换后的链表. 示例: 给定 1->2->3->4, 你应该返回 2->1->4->3. 说明: 你的算法只能 ...
- Mysql 实用语句记录
都是工作中遇到的需求,但不是常用sql,特此记录,方便以后使用: 1.将指定列的数据拼起来存到某一列 UPDATE table_name SET b_col_name=CONCAT(b_col_nam ...
- [论文理解] Spatial Transformer Networks
Spatial Transformer Networks 简介 本文提出了能够学习feature仿射变换的一种结构,并且该结构不需要给其他额外的监督信息,网络自己就能学习到对预测结果有用的仿射变换.因 ...
- configprase模块,配置文件模块
import configparser # config = configparser.ConfigParser() # config["DEFAULT"] = {'Port':3 ...
- Pycharm 常用快捷键-Windows版
常用快捷键: Ctrl + / 行注释(可选中多行) Ctrl + Alt + L 代码格式化 Tab / Shift + Tab 缩进.不缩进当前行(可选中多行) Ctrl + D 复制选定的区域 ...
- Xpath 和Css Selector使用
Xpath是xml的路径语言,就是通过元素的路径来查找标签元素. Xpath直接在火狐浏览器的firebug中练习,49版本一下的火狐才能用firebug插件. Xpath的使用方法 注://* ...
- MEF引起的内存泄露
也许你编程的时候很小心,注意不引起内存泄露,例如不要被全局Static的变量引用上,注意Singleton的static引用,注意Event Handler注销,注意IDisposable接口实现,而 ...
- 我非要捅穿这 Neutron(三)架构分析与代码实现篇(基于 OpenStack Rocky)
目录 文章目录 目录 Neutron 的软件架构分析与实现 Neutron Server 启动流程 获取 WSGI Application Core API & Extension API C ...
- 阶段3 2.Spring_07.银行转账案例_1 今日课程内容介绍
1.完善我们的account案例 2.分析案例中问题 3.回顾之前讲过的一个技术:动态代理 4.动态代理另一种实现方式 5.解决案例中的问题 6.AOP的概念 7.spring中的AOP相关术语 8. ...
