AtCoder ABC 131F Must Be Rectangular!

题目链接：https://atcoder.jp/contests/abc131/tasks/abc131_f

转自博客：https://blog.csdn.net/qq_37656398/article/details/93496476

题目大意

　　给定 N 个点，若有如下图所示的三个点（黑点）就可以构造岀一个新的点（红点）。求可构造的点的最多的个数。

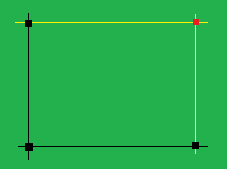
分析

　　首先，如果两个点的某一个坐标相等，我们定义这两个点是联通的。

　　其次，如果红点能够被构造，它必然是由处于同一连通块中的点所构造的。

　　于是，只要分别计算每个联通块能构造多少点就可以了。

　　对于每个连通块，把 x 坐标和 y 坐标单独弄一个集合，然后就在两个集合中不断分别取两个进行构造，直到不能构造为止，图示如下：

　　我们发现，构造的过程就是把构造前的二部图构造成完全二部图，每多一条边就表明构造了一个点。

　　于是把所有连通块所对应的完全二部图边数都加起来再减去 N 就能得到能构造的点的数目了。

代码如下

 #include <bits/stdc++.h>
 using namespace std;

 #define INIT() ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
 #define Rep(i,n) for (int i = 0; i < (n); ++i)
 #define For(i,s,t) for (int i = (s); i <= (t); ++i)
 #define rFor(i,t,s) for (int i = (t); i >= (s); --i)
 #define ForLL(i, s, t) for (LL i = LL(s); i <= LL(t); ++i)
 #define rForLL(i, t, s) for (LL i = LL(t); i >= LL(s); --i)
 #define foreach(i,c) for (__typeof(c.begin()) i = c.begin(); i != c.end(); ++i)
 #define rforeach(i,c) for (__typeof(c.rbegin()) i = c.rbegin(); i != c.rend(); ++i)

 #define pr(x) cout << #x << " = " << x << "  "
 #define prln(x) cout << #x << " = " << x << endl

 #define LOWBIT(x) ((x)&(-x))

 #define ALL(x) x.begin(),x.end()
 #define INS(x) inserter(x,x.begin())
 #define UNIQUE(x) x.erase(unique(x.begin(), x.end()), x.end())
 #define REMOVE(x, c) x.erase(remove(x.begin(), x.end(), c), x.end()); // 删去 x 中所有 c
 #define TOLOWER(x) transform(x.begin(), x.end(), x.begin(),::tolower);
 #define TOUPPER(x) transform(x.begin(), x.end(), x.begin(),::toupper);

 #define ms0(a) memset(a,0,sizeof(a))
 #define msI(a) memset(a,inf,sizeof(a))
 #define msM(a) memset(a,-1,sizeof(a))

 #define MP make_pair
 #define PB push_back
 #define ft first
 #define sd second

 template<typename T1, typename T2>
 istream &operator>>(istream &in, pair<T1, T2> &p) {
     in >> p.first >> p.second;
     return in;
 }

 template<typename T>
 istream &operator>>(istream &in, vector<T> &v) {
     for (auto &x: v)
         in >> x;
     return in;
 }

 template<typename T1, typename T2>
 ostream &operator<<(ostream &out, const std::pair<T1, T2> &p) {
     out << "[" << p.first << ", " << p.second << "]" << "\n";
     return out;
 }

 inline int gc(){
     static const int BUF = 1e7;
     static char buf[BUF], *bg = buf + BUF, *ed = bg;

     if(bg == ed) fread(bg = buf, , BUF, stdin);
     return *bg++;
 } 

 inline int ri(){
     int x = , f = , c = gc();
     for(; c<||c>; f = c=='-'?-:f, c=gc());
     for(; c>&&c<; x = x* + c - , c=gc());
     return x*f;
 }

 template<class T>
 inline string toString(T x) {
     ostringstream sout;
     sout << x;
     return sout.str();
 }

 inline int toInt(string s) {
     int v;
     istringstream sin(s);
     sin >> v;
     return v;
 }

 //min <= aim <= max
 template<typename T>
 inline bool BETWEEN(const T aim, const T min, const T max) {
     return min <= aim && aim <= max;
 }

 typedef long long LL;
 typedef unsigned long long uLL;
 typedef pair< double, double > PDD;
 typedef pair< int, int > PII;
 typedef pair< int, PII > PIPII;
 typedef pair< string, int > PSI;
 typedef pair< int, PSI > PIPSI;
 typedef set< int > SI;
 typedef set< PII > SPII;
 typedef vector< int > VI;
 typedef vector< double > VD;
 typedef vector< VI > VVI;
 typedef vector< SI > VSI;
 typedef vector< PII > VPII;
 typedef map< int, int > MII;
 typedef map< int, string > MIS;
 typedef map< int, PII > MIPII;
 typedef map< PII, int > MPIII;
 typedef map< string, int > MSI;
 typedef map< string, string > MSS;
 typedef map< PII, string > MPIIS;
 typedef map< PII, PII > MPIIPII;
 typedef multimap< int, int > MMII;
 typedef multimap< string, int > MMSI;
 //typedef unordered_map< int, int > uMII;
 typedef pair< LL, LL > PLL;
 typedef vector< LL > VL;
 typedef vector< VL > VVL;
 typedef priority_queue< int > PQIMax;
 typedef priority_queue< int, VI, greater< int > > PQIMin;
 const double EPS = 1e-;
 const LL inf = 0x7fffffff;
 const LL infLL = 0x7fffffffffffffffLL;
 const LL mod = 1e9 + ;
 const int maxN = 1e5 + ;
 const LL ONE = ;
 const LL evenBits = 0xaaaaaaaaaaaaaaaa;
 const LL oddBits = 0x5555555555555555;

 int N, K, M;
 LL ans;

 int f[maxN << ], sz[maxN << ][];

 int Find(int x){
     while (x != f[x]) x = f[x] = f[f[x]];
     return x;
 } 

 int main(){
     //freopen("MyOutput.txt","w",stdout);
     //freopen("input.txt","r",stdin);
     //INIT();
     cin >> N;
     Rep(i, maxN << ) f[i] = i;

     Rep(i, N) {
         int x, y;
         cin >> x >> y;
         y += maxN;
         f[Find(x)] = Find(y);
     }
     Rep(i, maxN << ) ++sz[Find(i)][i / maxN];
     Rep(i, maxN << ) ans += (LL)sz[i][] * sz[i][];
     cout << ans - N << endl;
     return ;
 }