[CSP-S模拟测试]:Lighthouse（哈密顿回路+容斥）

题目背景

$Billions\ of\ lighthouses...stuck\ at\ the\ far\ end\ of\ the\ sky.$

---

题目描述

平面有$n$个灯塔，初始时两两之间可以相互交流；但由于地形原因，有$m$对灯塔之间无法进行直接的交流。也就是一张完全图缺少了$m$条边。
    $River$想把这$n$个灯塔连成一个环，使得$n$个等他都在环上，并且环上相邻的两个灯塔能进行直接交流。$River$想知道这样做的方案数是多少，两种方案被认为是不同的，当且仅当有两个灯塔$u,v$，他们在一种方案中在环上相邻，而在另一种方案中相反。
    答案可能很大，你只需要输出对${10}^9+7$取模的结果。

---

输入格式

第一行两个整数$n,m$。
接下来$m$行，每行描述一条缺少的边。

---

输出格式

一行一个整数表示答案。

---

样例

样例输入1：

4 1
1 2

样例输出1：

1

样例输入2：

10 3
1 9
3 8
2 7

样例输出2：

87840

---

数据范围与提示

样例$1$解释：

唯一的方案是(1,3,2,4)依次连成环。

数据范围：

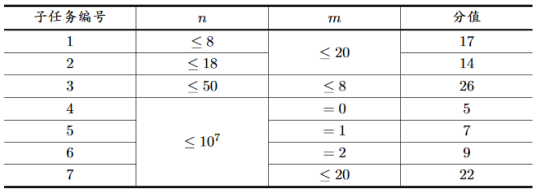
对于所有数据，有$3\leqslant n\leqslant {10}^7,0\leqslant m\leqslant \min(20,\frac{n(n-1)}{2})$。输入的边中没有重边。

---

题解

题目实际上球的就是哈密顿回路的数量。由于$m$很小，考虑容斥。
    枚举删除的边的某个子集$S$，设$f_S$表示有多少条哈密顿回路至少包含$S$集合中的边，答案就是$\sum_S(-1)^{|S|}\times f_S$。
    怎么算$f_S$呢？首先判掉$f_S=0$的情况，这包含以下两种情况：
        $\alpha.$仅考虑$S$中的边时，某个点的度数大于$2$。
        $\beta.$出现了环，并且这个环的大小不为$n$。
    特判掉$S$本身就是一个哈密顿回路的情况；假设$S$中的边构成了$k$条链，那么$f_S=s{k-1}\times (n-|S|-1)!$。
    证明：考虑将一条链看成一个点，那么总共有$n-|S|$个点，其环排列方案数为$(n-|S|-1)!$；每条链都可以翻转，因此乘上$2^k$；又由于一条哈密顿回路对应了两个环排列（正反两个方向），还要除以$2$。

时间复杂度：$\Theta(2^m\times m)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n,m;
long long jc[10000001];
int fa[10000001];
pair<int,int> pos[10000001];
int tot;
long long ans;
int cnt[10000001],vis[10000001],g[10000001];
int que[10000001];
map<pair<int,int>,bool> h;
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
long long qpow(long long x,long long y)
{long long res=1;while(y){if(y&1)res=res*x%1000000007;x=x*x%1000000007;y>>=1;}return res;}
long long solve(int x)
{
	int sum=0,k=que[0]=0;
	bool flag=0;
	for(int i=1;i<=tot;i++)
		if((x>>(i-1))&1)
		{
			que[++que[0]]=i;
			fa[pos[i].first]=pos[i].first;
			fa[pos[i].second]=pos[i].second;
			vis[pos[i].first]=vis[pos[i].second]=g[pos[i].first]=g[pos[i].second]=0;
		}
	for(int i=1;i<=que[0];i++)
	{
		if(!vis[pos[que[i]].first])sum++;
		if(!vis[pos[que[i]].second])sum++;
		if(vis[pos[que[i]].first]==2||vis[pos[que[i]].second]==2)return 0LL;
		vis[pos[que[i]].first]++;
		vis[pos[que[i]].second]++;
	}
	for(int i=1,u,v;i<=que[0];i++)
	{
		if((u=find(pos[que[i]].first))==(v=find(pos[que[i]].second)))flag=1;
		fa[u]=v;
	}
	for(int i=1,u;i<=que[0];i++)
		if(!g[u=find(pos[que[i]].first)]){g[u]=1;k++;}
	if(flag&&(cnt[x]!=n||k>1))return 0LL;
	long long res=jc[n-sum+k-1]*qpow(2,k)%1000000007*qpow(2,1000000005)%1000000007;
	return (cnt[x]&1)?-res:res;
}
int main()
{
	jc[0]=1;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		if(x==y||h[make_pair(x,y)])continue;
		h[make_pair(x,y)]=1;
		pos[++tot]=make_pair(x,y);
	}
	for(int i=1;i<=n;i++)jc[i]=1LL*i*jc[i-1]%1000000007;
	for(int i=0;i<(1<<tot);i++)cnt[i]=cnt[i>>1]+(i&1);
	for(int i=0;i<(1<<tot);i++)ans=(ans+solve(i))%1000000007;
	printf("%lld",(ans+1000000007)%1000000007);
	return 0;
}

---

rp++