Pollard Rho 算法简介

\(\text{update 2019.8.18}\) 由于本人将大部分精力花在了cnblogs上，而不是洛谷博客，评论区提出的一些问题直到今天才解决。

下面给出的Pollard Rho函数已给出散点图。关于\(Millar Robin\)算法的时间复杂度在我的博客应该有所备注。由于本人不擅长时间复杂度分析，如果对于时间复杂度有任何疑问，欢迎在下方指出。

1.1 问题的引入

给定一正整数\(N \in \mathbb{N}^*\),试快速找到它的一个因数。

很久很久以前，我们曾学过试除法来解决这个问题。很容易想到因数是成对称分布的：即\(N\)的所有因数可以被分成两块：\([1,\sqrt(N)]\)和\([\sqrt(N),N]\).这个很容易想清楚,我们只需要把区间\([1,\sqrt(N)]\)扫一遍就可以了,此时试除法的时间复杂度为\(O(\sqrt(N))\).

对于\(N \geqslant 10^{18}\)的数据,这个算法运行起来无意是非常糟糕的.我们希望有更快的算法,比如\(O(1)\)级别的?

对于这样的算法,一个比较好的想法是去设计一个随机程序,随便猜一个因数.如果你运气好,这个程序的时间复杂度下限为\(o(1)\).但对于一个\(N \geqslant 10^{18}\)的数据,这个算法给出答案的概率是\(\frac{1}{1000000000000000000}\).当然,如果在\([1,\sqrt(N)]\)里面猜,成功的可能性会更大.

那么,有没有更好的改进算法来提高我们猜的准确率呢?

2.1 用一个悖论来提高成功率

我们来考虑这样一种情况:在\([1,1000]\)里面取一个数,取到我们想要的数(比如说,\(42\)),成功的概率是多少呢?显然是\(\frac{1}{1000}\).

一个不行就取两个吧:随便在\([1,1000]\)里面取两个数.我们想办法提高准确率,就取两个数的差值绝对值.也就是说,在\([1,1000]\)里面任意选取两个数\(i , j\),问\(|i-j|=42\)的概率是多大?答案会扩大到\(\frac{1}{500}\)左右,也就是将近扩大一倍.机房的gql大佬给出了简证:\(i\)在\([1,1000]\)里面取出一个正整数的概率是\(100\%\),而取出\(j\)满足\(|i-j|=42\)的概率差不多就是原来的一倍:\(j\)取\(i-42\)和\(i+42\)都是可以的.

这给了我们一点启发:这种"组合随机采样"的方法是不是可以大大提高准确率呢?

这个便是生日悖论的模型了.假如说一个班上有k个人,如果找到一个人的生日是4月2日,这个概率的确会相当低.但是如果单纯想找到两个生日相同的人,这个概率是不是会高一点呢?

可以暴力证明:如果是\(k\)个人生日互不相同,则概率为:\(p=\frac{365}{365}\cdot\frac{364}{365}\cdot\frac{363}{365}\cdot\dots\cdot\frac{365-k+1}{365}\) ,故生日有重复的现象的概率是:\(\text{P}(k)=1-\prod\limits_{i=1}^{k}{\frac{365-i+1}{365}}\).

我们随便取一个概率:当\(P(k) \geqslant \frac{1}{2}\)时,解得\(k \gtrsim 23\).这意味着一个有23个人组成的班级中,两个人在同一天生日的概率至少有\(50\%\)!当k取到60时,\(\text{P}(k) \approx 0.9999\).这个数学模型和我们日常的经验严重不符.这也是"生日悖论"这个名字的由来.

3.1 随机算法的优化

生日悖论的实质是:由于采用"组合随机采样"的方法,满足答案的组合比单个个体要多一些.这样可以提高正确率.

我们不妨想一想:如何通过组合来提高正确率呢?有一个重要的想法是:最大公约数一定是某个数的约数.也就是说,\(\forall k \in \mathbb{N}^* , \gcd(k,n)|n\).只要选适当的k使得\(\gcd(k,n)>1\)就可以求得一个约数\(\gcd(k,n)\).这样的k数量还是蛮多的:k有若干个质因子,而每个质因子的倍数都是可行的.

我们不放选取一组数\(x_1,x_2,x_3,\dots,x_n\),若有\(gcd(|x_i-x_j|,N)>1\),则称\(gcd(|x_i-x_j|,N)\)是N的一个因子.早期的论文中有证明,需要选取的数的个数大约是\(O(N^{\frac{1}{4}})\).但是,我们还需要解决储存方面的问题.如果\(N=10^{18}\),那么我们也需要取\(10^4\)个数.如果还要\(O(n^2)\)来两两比较,时间复杂度又会弹回去.

3.2 Pollard Rho 和他的随机函数

我们不妨考虑构造一个伪随机数序列,然后取相邻的两项来求gcd.为了生成一串优秀的随机数,Pollard设计了这样一个函数:

\(f(x)=(x^2+c)\mod N\)

其中c是一个随机的常数.

我们随便取一个\(x_1\),令\(x_2=f(x_1)\),\(x_3=f(x_2)\),\(\dots\),\(x_i=f(x_{i-1})\).在一定的范围内,这个数列是基本随机的,可以取相邻两项作差求gcd.

生成伪随机数的方式有很多种.但是这个函数生成出来的伪随机数效果比较好.它的图像长这个样子:

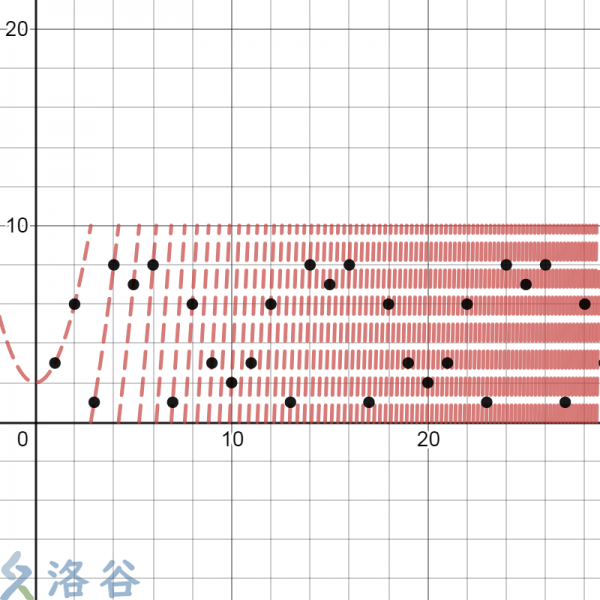
这里的函数为\(f(x)=(x^2+2)\mod 10\)。图中的黑点为迭代\(1,2,\cdots,30\)次得到的随机数。其实从这里很容易看出一个重复3次的循环节。

选取这个函数是自有道理的.有一种几何图形叫做曼德勃罗集,它是用\(f(x)=x^2+c\),然后带入复数,用上面讲到的方式进行迭代的.



↑曼德勃罗集.每个点的坐标代表一个复数\(x_1\),然后根据数列的发散速度对这个点染色.

这个图形和所谓的混沌系统有关.我猜大概是混沌这个性质保证了Pollard函数会生成一串优秀的伪随机数吧.

不过之所以叫伪随机数,是因为这个数列里面会包含有"死循环".

\({1,8,11,8,11,8,11,\dots}\)这个数列是\(c=7,N=20,x_1=1\)时得到的随机数列.这个数列会最终在8和11之间不断循环.循环节的产生不难理解:在模N意义下,整个函数的值域只能是\({0,1,2,\dots,N-1}\).总有一天,函数在迭代的过程中会带入之前的值,得到相同的结果.

生成数列的轨迹很像一个希腊字母\(\rho\),所以整个算法的名字叫做Pollard Rho.

3.3 基于Floyd算法优化的Pollard Rho

为了判断环的存在,可以用一个简单的Floyd判圈算法,也就是"龟兔赛跑".

假设乌龟为\(t\),兔子为\(r\),初始时\(t=r=1\).假设兔子的速度是乌龟的一倍.

过了时间\(i\)后,\(t=i,r=2i\).此时两者得到的数列值\(x_t=x_i,x_r=x_{2i}\).

假设环的长度为\(c\),在环内恒有:\(x_i=x_{i+c}\).

如果龟兔"相遇",此时有:\(x_r=x_t\),也就是\(x_i=x_{2i}=x_{i+kc}\).此时两者路径之差正好是环长度的整数倍。

这样以来,我们得到了一套基于Floyd判圈算法的Pollard Rho 算法.

int f(int x,int c,int n)
{
    return (x*x+c)%n;
}

int pollard_rho(int N)
{
    int c=rand()%(N-1)+1;
    int t=f(0,c,N),r=f(f(0,c,N),c,N);//两倍速跑
    while(t!=r)
    {
        int d=gcd(abs(t-r),N);
        if(d>1)
            return d;
        t=f(t,c,N),r=f(f(r,c,N),c,N);
    }
    return N;//没有找到,重新调整参数c
}

3.4 基于路径倍增和一个常数的优化

由于求\(\gcd\)的时间复杂度是\(O(\log{N})\)的,频繁地调用这个函数会导致算法变得异常慢.我们可以通过乘法累积来减少求gcd的次数.

显然的,如果\(\gcd(a,b)>1\),则有\(\gcd(ac,b)>1\),c是某个正整数.更近一步的,由欧几里得算法,我们有\(gcd(a,b) = gcd(ac\mod b,b) >1\). 我们可以把所有测试样本\(|t-r|\)在模N意义下乘起来,再做一次gcd.选取适当的相乘个数很重要.

我们不妨考虑倍增的思想:每次在路径\(\rho\)上倍增地取一段\([2^{k-1},2^k]\)的区间.将\(2^{k-1}\)记为\(l\),\(2^k\)记为\(r\).取而代之的,我们每次取的gcd测试样本为\(|x_i-x_l|\),其中\(l \leqslant i \leqslant r\).我们每次积累的样本个数就是\(2^{k-1}\)个,是倍增的了.这样可以在一定程度上避免在环上停留过久,或者取gcd的次数过繁的弊端.

当然，如果倍增次数过多，算法需要积累的样本就越多。我们可以规定一个倍增的上界。

↑\(127=2^7-1\)，据推测应该是限制了倍增的上界。

一旦样本的长度超过了127，我们就结束这次积累，并求一次\(\gcd\)。\(127\)这个数应该是有由来的。在最近一次学长考试讲解中，\(128\)似乎作为“不超过某个数的质数个数”出现在时间复杂度中。不过你也可以理解为，将"迭代7次"作为上界是实验得出的较优方案。如果有知道和\(128\)有关性质的大佬，欢迎在下方留言。

这样,我们就得到了一套完整的,基于路径倍增的Pollard Rho 算法.

inline ll PR(ll x)
{
    ll s=0,t=0,c=1ll*rand()%(x-1)+1;
    int stp=0,goal=1;
    ll val=1;
    for(goal=1;;goal<<=1,s=t,val=1)
    {
        for(stp=1;stp<=goal;++stp)
        {
            t=f(t,c,x);
            val=(lll)val*abs(t-s)%x;
            if((stp%127)==0)
            {
                ll d=gcd(val,x);
                if(d>1)
                    return d;
            }
        }
        ll d=gcd(val,x);
        if(d>1)
            return d;
    }
}

这个代码不一定是最好的,还可以有相当多的优化.不过至少它足够通过部分毒瘤数据了.

4.1 例题

P4718

这个问题还需要一个Miller Rabin测试来快速测定质数.

对于一个数\(n\),我们首先用Miller Rabin快速判定一下这个数是不是质数.如果是则直接返回,否则就用Pollard Rho 找一个因子p.

将n中的因子p全部删去,再递归地分解新的n和p.

可以用一个全局变量max_factor记录一下n最大的因子,在递归分解的时候就可以把没必要的操作"剪枝"掉.

#include<bits/stdc++.h>
using namespace std;
#define rg register
#define RP(i,a,b) for(register int i=a;i<=b;++i)
#define DRP(i,a,b) for(register int i=a;i>=b;--i)
#define fre(z) freopen(z".in","r",stdin),freopen(z".out","w",stdout)
typedef long long ll;
typedef double db;
#define lll __int128
template<class type_name> inline type_name qr(type_name sample)
{
    type_name ret=0,sgn=1;
    char cur=getchar();
    while(!isdigit(cur))
        sgn=(cur=='-'?-1:1),cur=getchar();
    while(isdigit(cur))
        ret=(ret<<1)+(ret<<3)+cur-'0',cur=getchar();
    return sgn==-1?-ret:ret;
}

ll max_factor;

inline ll gcd(ll a,ll b)
{
    if(b==0)
        return a;
    return gcd(b,a%b);
}

inline ll qp(ll x,ll p,ll mod)
{
    ll ans=1;
    while(p)
    {
        if(p&1)
            ans=(lll)ans*x%mod;
        x=(lll)x*x%mod;
        p>>=1;
    }
    return ans;
}

inline bool mr(ll x,ll b)
{
    ll k=x-1;
    while(k)
    {
        ll cur=qp(b,k,x);
        if(cur!=1 && cur!=x-1)
            return false;
        if((k&1)==1 || cur==x-1)
            return true;
        k>>=1;
    }
    return true;
}

inline bool prime(ll x)
{
    if(x==46856248255981ll || x<2)
        return false;
    if(x==2 || x==3 || x==7 || x==61 || x==24251)
        return true;
    return mr(x,2)&&mr(x,61);
}

inline ll f(ll x,ll c,ll n)
{
    return ((lll)x*x+c)%n;
}

inline ll PR(ll x)
{
    ll s=0,t=0,c=1ll*rand()%(x-1)+1;
    int stp=0,goal=1;
    ll val=1;
    for(goal=1;;goal<<=1,s=t,val=1)
    {
        for(stp=1;stp<=goal;++stp)
        {
            t=f(t,c,x);
            val=(lll)val*abs(t-s)%x;
            if((stp%127)==0)
            {
                ll d=gcd(val,x);
                if(d>1)
                    return d;
            }
        }
        ll d=gcd(val,x);
        if(d>1)
            return d;
    }
}

inline void fac(ll x)
{
    if(x<=max_factor || x<2)
        return;
    if(prime(x))
    {
        max_factor=max_factor>x?max_factor:x;
        return;
    }
    ll p=x;
    while(p>=x)
        p=PR(x);
    while((x%p)==0)
        x/=p;
    fac(x),fac(p);
}

int main()
{
    int T=qr(1);
    while(T--)
    {
        srand((unsigned)time(NULL));
        ll n=qr(1ll);
        max_factor=0;
        fac(n);
            if(max_factor==n)
                puts("Prime");
            else
                printf("%lld\n",max_factor);
    }
    return 0;
}