数据结构系列之2-3树的插入、查找、删除和遍历完整版代码实现（dart语言实现）

　　弄懂了二叉树以后，再来看2-3树。网上、书上看了一堆文章和讲解，大部分是概念，很少有代码实现，尤其是删除操作的代码实现。当然，因为2-3树的特性，插入和删除都是比较复杂的，因此经过思考，独创了删除时分支收缩、重新展开的算法，保证了删除后树的平衡和完整。该算法相比网上的实现相比，相对比较简洁；并且，重要的是，该删除算法可以推广至2-3-4树，甚至是多叉树。

————声明：原创，转载请说明来源————

一、2-3树的定义

　　2-3树是最简单的B-树（或-树）结构，其每个非叶节点都有两个或三个子女，而且所有叶都在统一层上。2-3树不是二叉树，其节点可拥有3个孩子。不过，2-3树与满二叉树相似。若某棵2-3树不包含3-节点，则看上去像满二叉树，其所有内部节点都可有两个孩子，所有的叶子都在同一级别。另一方面，2-3树的一个内部节点确实有3个孩子，故比相同高度的满二叉树的节点更多。高为h的2-3树包含的节点数大于等于高度为h的满二叉树的节点数，即至少有2^h-1个节点。换一个角度分析，包含n的节点的2-3树的高度不大于[log2(n+1)](即包含n个节点的二叉树的最小高度)。

　　下图显示高度为3的2-3树。包含两个孩子的节点称为2-节点，二叉树中的节点都是2-节点；包含三个孩子的节点称为3-节点。

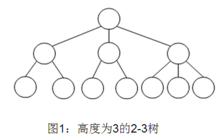
（图片来自网络）

　　先来看2-3树的节点的定义：

 class TerNode<E extends Comparable<E>> {
   static final int capacity = 2;
   List<E> items;
   List<TerNode<E>> branches;
   TerNode<E> parent;

   factory TerNode(List<E> elements) {
     if (elements.length > capacity) throw StateError('too many elements.');
     return TerNode._internal(elements);
   }

   TerNode._internal(List<E> elements)
       : items = [],
         branches = [] {
     items.addAll(elements);
   }

   int get size => items.length;
   bool get isOverflow => size > capacity;
   bool get isLeaf => branches.isEmpty;
   bool get isNotLeaf => !isLeaf;

   bool contains(E value) => items.contains(value);
   int find(E value) => items.indexOf(value);

   String toString() => items.toString();
 }

　　2-3树的定义：

 class TernaryTree<E extends Comparable<E>> {
   TerNode<E> _root;
   int _elementsCount;

   factory TernaryTree.of(Iterable<Comparable<E>> elements) {
     var tree = TernaryTree<E>();
     for (var e in elements) tree.insert(e);
     return tree;
   }

   TernaryTree() : _elementsCount = 0;

   // ...

 }

二、插入算法
　　首先，2-3树的插入，都是在叶子上完成的。首先定位查找I的操作的叶子，然后将新的元素插入至对应节点。插入后，需要判断是否需要修复，如果当前节点的元素个数大于2，则需要分裂；该节点分裂为三个节点，左、右元素为两个新的叶子节点，中间元素成为新的父节点；然后判断是否需要吸收新的父节点；递归向上，直至满足条件或直至根节点。

　　插入操作代码如下：

 void insert(E value) {
     var c = root, i = 0;
     while (c != null) {
       i = 0;
       while (i < c.size && c.items[i].compareTo(value) < 0) i++;
       if (i < c.size && c.items[i] == value) return;
       if (c.isLeaf) break;
       c = c.branches[i];
     }
     if (c != null) {
       c.items.insert(i, value);
       if (c.isOverflow) _fixAfterIns(c);
     } else {
       _root = TerNode([value]);
     }
     _elementsCount++;
   }

　　注意 该行代码，判断是否需要修复：

 if (c.isOverflow) _fixAfterIns(c);

　　如果需要修复，则进行节点分裂、吸收，递归至根节点或不再溢出的节点为止，修复代码如下：

 void _fixAfterIns(TerNode<E> c) {
     while (c != null && c.isOverflow) {
       var t = _split(c);
       c = t.parent != null ? _absorb(t) : null;
     }
   }

   TerNode<E> _split(TerNode<E> c) {
     var mid = c.size ~/ 2,
         l = TerNode._internal(c.items.sublist(0, mid)),
         nc = TerNode._internal(c.items.sublist(mid, mid + 1)),
         r = TerNode._internal(c.items.sublist(mid + 1));
     nc.branches.addAll([l, r]);
     l.parent = r.parent = nc;

     nc.parent = c.parent;
     if (c.parent != null) {
       var i = 0;
       while (c.parent.branches[i] != c) i++;
       c.parent.branches[i] = nc;
     } else {
       _root = nc;
     }
     if (c.isNotLeaf) {
       l.branches
         ..addAll(c.branches.getRange(0, mid + 1))
         ..forEach((b) => b.parent = l);
       r.branches
         ..addAll(c.branches.getRange(mid + 1, c.branches.length))
         ..forEach((b) => b.parent = r);
     }
     return nc;
   }

   TerNode<E> _absorb(TerNode<E> c) {
     var i = 0, p = c.parent;
     while (p.branches[i] != c) i++;
     p.items.insertAll(i, c.items);
     p.branches.replaceRange(i, i + 1, c.branches);
     c.branches.forEach((b) => b.parent = p);
     return p;
   }

三、查找算法

　　查找实现比较简单，因为插入操作时，其实已经先进行了查找。代码如下：

 TerNode<E> find(E value) {
     var c = root;
     while (c != null) {
       var i = 0;
       while (i < c.size && c.items[i].compareTo(value) < 0) i++;
       if (i < c.size && c.items[i] == value) break;
       c = c.isNotLeaf ? c.branches[i] : null;
     }
     return c;
   }

四、删除算法

　　删除算法是最复杂的。

　　首先，为了降低复杂度，我们采用类似二叉树或红黑树一样的算法，如果待删除的元素存在且为非叶子节点的话，则用后继的叶子节点的值替代要删除的节点元素。此时则将删除问题转移到了叶子节点上，这样避免了孩子分支的处理。

　　其次，删除元素。删除后，判断是否需要修复。如果节点删除后不为空，则不需要；否则就需要修复。修复的核心思路是，将该节点的所有兄弟节点全部收缩至父节点，并记录收缩的次数；然后判断父节点的元素数量是否足够展开为一颗最小的平衡二叉树，如果不够，继续递归向上收缩，直至够了为止，或者到达根节点。如果倒达了根节点，则将树的高度减 1 ，进行展开。

　　如何判断一个节点的元素数量，满足展开为一颗最小的平衡二叉树？其实有个最简单的算法，一颗平衡二叉树的高度和元素个数，有如下规律：

高度为 1： 元素个数为 1 ，2^1  - 1 ；

高度为 2：元素个数为 3 ，2^2 - 1 ；

……

高度为 h:  元素个数为       2^h -1 ；

　　父节点收缩后重新展开，需要将多余的节点元素修剪掉，这些多余的节点元素，后续在插入到这棵树上即可。

　　删除代码如下：

 bool delete(E value) {
     var d = find(value);
     if (d == null) return false;
     var i = d.find(value);
     if (d.isNotLeaf) {
       var s = _successor(d.branches[i + 1]);
       d.items[i] = s.items[0];
       d = s;
       i = 0;
     }
     d.items.removeAt(i);
     _elementsCount--;
     if (d.items.isEmpty) _fixAfterDel(d);
     return true;
   }

　　查找后继节点代码如下：

 TerNode<E> _successor(TerNode<E> p) {
     while (p.isNotLeaf) p = p.branches[0];
     return p;
   }

　　修复代码如下：

 void _fixAfterDel(TerNode<E> d) {
     if (d == root) {
       _root = null;
     } else {
       var ct = 0;
       while (d.size < (1 << ct + 1) - 1 && d.parent != null) {
         _collapse(d.parent);
         d = d.parent;
         ct++;
       }
       // if (d.size < (1 << ct + 1) - 1) ct--;
       if (d == root) ct--;
       var rest = _prune(d, (1 << ct + 1) - 1);
       _expand(d, ct);
       for (var e in rest) insert(e);
     }
   }

　　父节点塌缩孩子分支的代码如下，这里要注意，因为在修复时是递归向上塌缩的，因此，塌缩时需要递归塌缩父节点的所有分支，注意父节点p的元素、分支的处理：

 void _collapse(TerNode<E> p) {
     if (p.isLeaf) return;
     for (var i = p.branches.length - 1; i >= 0; i--) {
       _collapse(p.branches[i]);
       p.items.insertAll(i, p.branches[i].items);
     }
     p.branches.clear();
   }

　　塌缩后，在重新展开之前，需要修剪掉多余的元素。因为修剪掉的元素后续还是要插入到树中的，因此，保留的元素要尽量的居中，以避免重新插入时产生过多的分裂动作。代码如下：

 List<E> _prune(TerNode<E> d, int least) {
     var t = d.size ~/ least, rest = <E>[];
     if (t < 2) {
       rest.addAll(d.items.getRange(least, d.size));
       d.items.removeRange(least, d.size);
     } else {
       var list = <E>[];
       for (var i = 0; i < d.size; i++) {
         if (i % t == 0 && list.length < least)
           list.add(d.items[i]);
         else
           rest.add(d.items[i]);
       }
       d.items = list;
     }
     _elementsCount -= rest.length;
     return rest;
   }

　　重新展开的代码如下，其实就是节点的递归向下分裂：

 void _expand(TerNode<E> p, int ct) {
     if (ct == 0) return;
     p = _split(p);
     for (var b in p.branches) _expand(b, ct - 1);
   }

　　删除操作至此完成。

　　最后，给一个判断树的高度的代码：

 int get height {
     var h = 0, c = root;
     while (c != null) {
       h++;
       c = c.isNotLeaf ? c.branches[0] : null;
     }
     return h;
   }

　　那么这些操作，是否每一步的插入或删除完成后，树仍然满足是一颗2-3树呢？测试验证代码如下：

List<E> a可以随机生成一个千万级的数组进行测试。如果要观看每一步的输出，把 print 前的注释拿掉即可。经过上亿次的验证，以上代码正确。
注意，dart 验证时，如果为非debug模式，则需要在terminal中加入 --enable-asserts参数，以打开assert开关。

 void ternaryTest<E extends Comparable<E>>(List<E> a) {
   var tree = TernaryTree.of(a);
   // print('check result: ${check(tree)}');
   check(tree);
   // print('-------------------');
   // print('a.lenght: ${a.length}, tree.elementsCount: ${tree.elementsCount}');
   // print('root: ${tree.root}  height: ${tree.height}');
   // stdin.readLineSync();
   // print('-------------------');
   // print('start to $i times ternary deleting test...');
   for (var e in a) {
     // print('-------------------');
     // print('delete: $e');
     tree.delete(e);
     // print('-------------------');
     // print('tree.elementsCount: ${tree.elementsCount}');
     // print('new root: ${tree.root}  height: ${tree.height}');
     // print('check result: ${check(tree)}');
     check(tree);
   }
 }

 bool check(TernaryTree tree) {
   if (!tree.isEmpty) assert(tree.height == _walk(tree.root));
   return true;
 }

 int _walk(TerNode r) {
   assert(!r.isOverflow);
   for (var i = 0; i + 1 < r.size; i++)
     assert(r.items[i].compareTo(r.items[i + 1]) < 0);

   if (r.isLeaf) return 1;
   assert(r.size + 1 == r.branches.length);
   var heights = <int>[];
   for (var b in r.branches) heights.add(_walk(b));
   for (var h in heights) assert(h == heights.first);
   return heights.first + 1;
 }

　　本来准备结束了，发现忘了给遍历函数了：

 void traverse(void func(List<E> items)) {
     if (!isEmpty) _traverse(_root, func);
   }

 void _traverse(TerNode<E> r, void f(List<E> items)) {
     f(r.items);
     for (var b in r.branches) _traverse(b, f);
   }