模拟赛T5 ： domino ——深搜+剪枝+位运算优化

这道题涉及的知识点有点多。。。

所以还是比较有意思的。

domino

描述

迈克生日那天收到一张 N*N 的表格(1 ≤ N ≤ 2000)，每个格子里有一个非

负整数（整数范围 0~1000），迈克不喜欢数值太大，他手上有 K 块日字形多米

诺骨牌（1 ≤ K ≤ 8），可以完美覆盖两个相邻格子（上下左右均可）**

问迈克把 K 块骨牌全部放在表格上，使得表格可见整数和最小。

输入

第一行两个数 N，K 用空格隔开 下面 N 行 N 列为该初始表格。

输出

被 K 块骨牌挡住之后剩余数字之和。

分数分布

对于 70%数据，K≤5。

样例输入 1

3 1

2 7 6

9 5 1

4 3 8

样例输出 1

31

样例输入 2

4 2

1 2 4 0

4 0 5 4

0 3 5 1

1 0 4 1

样例输出 2

17

解释下题意，在棋盘上放上k个1*2的骨牌,使覆盖到的格子上的值得和最大。

乍一看，貌似可以贪心，枚举所有骨牌，选择前k大的骨牌。（接下来骨牌大小的定义都是它覆盖的格子的和的大小）。但第二个样例却过不到。

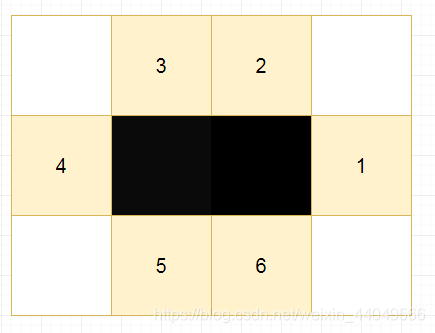
原因很简单，当我们选择了一个骨牌时，会导致顶多7个骨牌不能被选择，如图所示：



(这个骨牌自身也算一个)

如果我们选取的前k大个骨牌在这7个骨牌之中，则不合法，所以导致了错误。

所以我们可以将这7个骨牌全都加入在我们考虑选择的骨牌之中。于是我们考虑的骨牌最多便有了\(50\)个\((7*(8-1)+1)\)

考虑在这\(50\)个骨牌中间深搜，选择其中的\(k\)个，并且保证这些骨牌不会相互覆盖即可。

于是我们就将问题转换成了从50个物品中选出K个，使和最大，同时选择一个物品会导致多个物品不能选择的问题。这明显可以使用状压DP暴力解决。

但是直接暴力会超时，时间复杂度为\(2^{50}\)，空间复杂度也实在难以接受。

可以先看看我暴力的代码。

//感觉很好理解所以没怎么打注释
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;

#define N 2010

int A[N][N],n,k,P,siz;
bool mark[51][51];

struct node {
    LL x,y,sum,dir;//使用node来存储每个骨牌
    node() {};	   //x,y表示这个骨牌左上的坐标
    node(LL X,LL Y,LL D) {
        x=X;y=Y;
        sum=A[x][y]+A[x+D][y+1-D];//使用dir变量来表示可能的
        dir=D;					  //两种骨牌
    }
};

vector<node> L;

vector< pair<LL,LL> > getFuck(node F) {//返回一个vector生成
    vector<pair<LL,LL> > D;	//一个骨牌的两个坐标
    D.push_back( make_pair(F.x,F.y));
    D.push_back( make_pair(F.x+F.dir,F.y+1-F.dir));
    return D;
}

bool Fuck(node A,node B) {
    vector< pair<LL,LL> > X=getFuck(A);
    vector< pair<LL,LL> > Y=getFuck(B);
    for(LL i=0;i<X.size();i++)//判断两个骨牌的4个覆盖区域的
        for(LL j=0;j<Y.size();j++)//坐标是否重复
            if(X[i]==Y[j])
                return 1;
    return 0;
}

bool cmp(node A,node B) {
 return A.sum>B.sum;
}

int ans,sum;
bool vis[60];

void dfs(int pos,int haveC) {//暴力深搜，枚举选和不选当前骨牌的情况
    ans=max(ans,sum);
    if(pos==siz) return ;
    dfs(pos+1,haveC);
    if(haveC==k) return ;
    for(int i=0;i<pos;i++) if(vis[i] && mark[pos][i]) return ;
    vis[pos]=1;
    sum+=L[pos].sum;
    vis[pos]=1;
    dfs(pos+1,haveC+1);
    vis[pos]=0;
    sum-=L[pos].sum;
}

int main() {//基操
    cin>>n>>k;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            cin>>A[i][j],P+=A[i][j];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++) {
            if(i<n) L.push_back(node(i,j,1));
            if(j<n) L.push_back(node(i,j,0));
        }
    sort(L.begin(),L.end(),cmp);
    //for(int i=0;i<L.size();i++) cout<<L[i].sum<<' ';
    //cout<<endl;
    int Sz=L.size();
    siz=min(Sz,50);
    for(int i=0;i<siz;i++)
        for(int j=0;j<siz;j++)
            if(i!=j && Fuck(L[i],L[j]))
                mark[i][j]=1;
    dfs(0,0);
    cout<<P-ans;
    return 0;

正解用的是双向DFS，但我剪了下枝，发现用位运算也可以卡过去。

#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;

#define N 2010
#define LL long long
LL A[N][N],n,k,P,siz,lol;
LL mark[51];

struct node {
    LL x,y,sum,dir;
    node() {};
    node(LL X,LL Y,LL D) {
        x=X;y=Y;
        sum=A[x][y]+A[x+D][y+1-D];
        dir=D;
    }
};

vector<node> L;

vector< pair<LL,LL> > getFuck(node F) {
    vector<pair<LL,LL> > D;
    D.push_back( make_pair(F.x,F.y));
    D.push_back( make_pair(F.x+F.dir,F.y+1-F.dir));
    return D;
}

bool Fuck(node A,node B) {
    vector< pair<LL,LL> > X=getFuck(A);
    vector< pair<LL,LL> > Y=getFuck(B);
    for(LL i=0;i<X.size();i++)
        for(LL j=0;j<Y.size();j++)
            if(X[i]==Y[j])
                return 1;
    return 0;
}

bool cmp(node A,node B) {
 return A.sum>B.sum;
}

LL ans,sum;

void dfs(LL pos,LL haveC,LL cover) {
    ans=max(ans,sum);
    if(pos==siz) return ;
    if(haveC==k) return ;
    dfs(pos+1,haveC,cover);
    if(!(cover & (1ll<<pos))) {
        sum+=L[pos].sum;
        dfs(pos+1,haveC+1,cover|mark[pos]);
        sum-=L[pos].sum;
    }
}

int main() {
    cin>>n>>k;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            cin>>A[i][j],P+=A[i][j];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++) {
            if(i<n) L.push_back(node(i,j,1));
            if(j<n) L.push_back(node(i,j,0));
        }
    sort(L.begin(),L.end(),cmp);
    lol=L[0].sum;
    //for(int i=0;i<L.size();i++) cout<<L[i].sum<<' ';
    //cout<<endl;
    LL Sz=L.size();
    siz=min(Sz,(LL)50);
    for(int i=0;i<siz;i++)
        for(int j=0;j<siz;j++)
            if(i!=j && Fuck(L[i],L[j]))
                mark[i]|=(1ll<<j);
    dfs(0,0,0);
    cout<<P-ans;
    return 0;
}

说下我在做这题时的细节吧

1.所有变量尽量都要开long long，因为答案最终有可能爆int

2.第一部分不一定要占一半，开1<<20不会爆空间。

3.位运算要使用\(1ll<<50\).

这里附上双向DFS的代码，有兴趣的同学可以康康，注释写得挺详细的。

(估计也没人看吧hhh)

#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;

#define N 2010
#define LL long long

LL A[N][N],n,k,P,siz,asiz,bsiz;
LL mark[54];
LL FFuck[1<<21][9],ans;

struct node {
    LL x,y,sum,dir;
    node() {};
    node(LL X,LL Y,LL D) {
        x=X;y=Y;
        sum=A[x][y]+A[x+D][y+1-D];
        dir=D;
    }
};

vector<node> L;

vector< pair<LL,LL> > getFuck(node F) {
    vector<pair<LL,LL> > D;
    D.push_back( make_pair(F.x,F.y));
    D.push_back( make_pair(F.x+F.dir,F.y+1-F.dir));
    return D;
}

bool Fuck(node A,node B) {
    vector< pair<LL,LL> > X=getFuck(A);
    vector< pair<LL,LL> > Y=getFuck(B);
    for(LL i=0;i<X.size();i++)
        for(LL j=0;j<Y.size();j++)
            if(X[i]==Y[j])
                return 1;
    return 0;
}

bool cmp(node A,node B) {
 return A.sum>B.sum;
}

//дµÃÕæ³ó¹þ¹þ¹þ
void dfs1(LL pos,LL haveC,LL state,LL cover,LL sum) {
    if(haveC>k) return ;
    if(pos==asiz) {
        FFuck[state][haveC]=max(FFuck[state][haveC],sum);
        return ;
    }
    dfs1(pos+1,haveC,state,cover,sum);
    if(!(cover & (1ll<<pos))) {//
        LL mss=L[pos].sum;
        dfs1(pos+1,haveC+1,state|(1ll<<pos),cover|mark[pos],sum+mss);
    }
}

void dfs2(LL pos,LL haveC,LL state,unsigned LL cover,LL sum) {
    if(haveC>k) return ;
    if(pos==siz) {
        ans=max(ans,sum+FFuck[(~cover)&((1ll<<asiz)-1)][k-haveC]);
        return ;
    }
    dfs2(pos+1,haveC,state,cover,sum);
    if(!(cover & (1ll<<pos))) {
        LL mss=L[pos].sum;
        dfs2(pos+1,haveC+1,state|(1ll<<pos),cover|mark[pos],sum+mss);
    }
}

int main() {
    cin>>n>>k;
    if(n==1) {cout<<0; return 0;}
    LL MM=(k-1)*7+1;
    for(LL i=1;i<=n;i++)
        for(LL j=1;j<=n;j++)
            cin>>A[i][j],P+=A[i][j];
    for(LL i=1;i<=n;i++)
        for(LL j=1;j<=n;j++) {
            if(i<n) L.push_back(node(i,j,1));
            if(j<n) L.push_back(node(i,j,0));
        }
    sort(L.begin(),L.end(),cmp);
    //for(LL i=0;i<L.size();i++) cout<<L[i].sum<<' ';
    //cout<<endl;
    LL Sz=L.size();
    siz=min(Sz,MM);
    asiz=min(siz/2,(LL)20);
    for(LL i=0;i<siz;i++)
        for(LL j=0;j<siz;j++)
            if(i!=j && Fuck(L[i],L[j]))
                mark[i]|=(1ll<<j);
    dfs1(0,0,0,0,0);
    for(LL c=0;c<=k;c++) {
        for(LL i=1;i<(1ll<<asiz);i++) {
            LL j=i;
            while(j) {
                LL t=j&-j;
                FFuck[i][c]=max(FFuck[i-t][c],FFuck[i][c]);
                j-=t;
            }
        }
    }
    dfs2(asiz,0,0,0,0);
    cout<<P-ans;
    return 0;
}