LR为什么用极大似然估计，损失函数为什么是log损失函数（交叉熵）

首先，逻辑回归是一个概率模型，不管x取什么值，最后模型的输出也是固定在（0,1）之间，这样就可以代表x取某个值时y是1的概率

这里边的参数就是θ，我们估计参数的时候常用的就是极大似然估计，为什么呢？可以这么考虑

比如有n个x，xi对应yi=1的概率是pi，yi=0的概率是1-pi，当参数θ取什么值最合适呢，可以考虑

n个x中对应k个1，和（n-k）个0（这里k个取1的样本是确定的，这里就假设前k个是1，后边的是0.平时训练模型拿到的样本也是确定的，如果不确定还要排列组合）

则(p1*p2*...*pk)*(1-pk+1)*(1-pk+2)*...*(1-pn)最大时，θ是最合适的。联合概率最大嘛，就是总体猜的最准，就是尽可能使机器学习中所有样本预测到对应分类得概率整体最大化。

其实上边的算式就是极大似然估计的算式：

对应到LR中：

总之就是因为LR是概率模型，对概率模型估计参数用极大似然，原理上边说了

然后为什么用logloss作为cost function呢

主要的原因就是因为似然函数的本质和损失函数本质的关系

对数似然函数：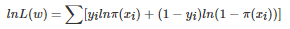

可以看到对数似然函数和交叉熵函数在二分类的情况下形式是几乎一样的，可以说最小化交叉熵的本质就是对数似然函数的最大化。

对数似然函数的本质就是衡量在某个参数下，整体的估计和真实情况一样的概率，越大代表越相近

而损失函数的本质就是衡量预测值和真实值之间的差距，越大代表越不相近。

他们两个是相反的一个关系，至于损失函数的惩罚程度，可以用参数修正，我们这里不考虑。

所以在对数似然前边加一个负号代表相反，这样就把对数似然转化成了一个损失函数，然后把y取0和1的情况分开（写成分段函数），就是：

意义就是：当y=1时，h=1时没有损失，h越趋近0损失越大

当y=0时，h=0没有损失，h越趋近1损失越大。