POJ 2112 Optimal Milking ( 经典最大流 && Floyd && 二分 )

题意 : 有 K 台挤奶机器，每台机器可以接受 M 头牛进行挤奶作业，总共有 C 头奶牛，机器编号为 1~K，奶牛编号为 K+1 ~ K+C ，然后给出奶牛和机器之间的距离矩阵，要求求出使得每头牛都能被安排到某一挤奶机且所有奶牛走出来的路径的最大值的最小值。

分析 : 一个比较复杂的最小化最大值问题，解题思路是二分路程花费，然后建图使用最大流判断可行性。当然还可以使用最小费用最大流，增广和最短路的松弛维护的就是路径上的最大值而不再是花费了。这里只讨论二分＋最大流解法，最小费用最大流的坑以后再填........

其实这题的思路和 POJ 2391 差不多 ==> 解题报告

先将题目给出来的距离矩阵跑一下 Floyd 求出全源最短路方便后面建图，这里注意一下除了对角线的点若有其他点为 0 则应将其值设置为 INF 代表不可达

抽象出一个源点和汇点，然后给安排出 C 个点代表 C 头牛、安排 K 个点代表 K 个挤奶机器，将源点到牛所代表的 C 个点各连一条容量为 1 的边

然后二分答案，对于二分出来的花费我们可以根据 Floyd 跑出来的距离矩阵将牛与机器之间的符合条件的( 最短花费 <= 当前二分的花费 )边连上

最后将各个机器与汇点连一条容量为 M 的边，以达到限制每台机器只接受 M 头牛这一限制，最后跑一下最大流，如果最大流 == 牛的总数说明可行

#include<stdio.h>
#include<queue>
#include<vector>
#include<algorithm>
#include<string.h>
using namespace std;
;
const int  INF = 0x3f3f3f3f;
int Dist[maxn][maxn];
int K, C, M;
 
struct Edge
{
    int from,to,cap,flow;
    Edge(){}
    Edge(int from,int to,int cap,int flow):from(from),to(to),cap(cap),flow(flow){}
 
};
 
struct Dinic
{
    int n,m,s,t;            //结点数,边数(包括反向弧),源点与汇点编号
    vector<Edge> edges;     //边表 edges[e]和edges[e^1]互为反向弧
    vector<int> G[maxn];    //邻接表,G[i][j]表示结点i的第j条边在e数组中的序号
    bool vis[maxn];         //BFS使用,标记一个节点是否被遍历过
    int d[maxn];            //d[i]表从起点s到i点的距离(层次)
    int cur[maxn];          //cur[i]表当前正访问i节点的第cur[i]条弧
 
    void init(int n,int s,int t)
    {
        this->n=n,this->s=s,this->t=t;
        ;i<=n;i++) G[i].clear();
        edges.clear();
    }
 
    void AddEdge(int from,int to,int cap)
    {
        edges.push_back( Edge() );
        edges.push_back( Edge(to,,) );
        m = edges.size();
        G[);
        G[to].push_back(m-);
    }
 
    bool BFS()
    {
        memset(vis,,sizeof(vis));
        queue<int> Q;//用来保存节点编号的
        Q.push(s);
        d[s]=;
        vis[s]=true;
        while(!Q.empty())
        {
            int x=Q.front(); Q.pop();
            ; i<G[x].size(); i++)
            {
                Edge& e=edges[G[x][i]];
                if(!vis[e.to] && e.cap>e.flow)
                {
                    vis[e.to]=true;
                    d[e.to] = d[x]+;
                    Q.push(e.to);
                }
            }
        }
        return vis[t];
    }
 
    //a表示从s到x目前为止所有弧的最小残量
    //flow表示从x到t的最小残量
    int DFS(int x,int a)
    {
        //printf("%d %d\n", x, a);
        )return a;
        ,f;//flow用来记录从x到t的最小残量
        for(int& i=cur[x]; i<G[x].size(); i++)
        {
            Edge& e=edges[G[x][i]];
            ==d[e.to] && (f=DFS( e.to,min(a,e.cap-e.flow) ) )> )
            {
                e.flow +=f;
                edges[G[x][i]^].flow -=f;
                flow += f;
                a -= f;
                ) break;
            }
        }
        return flow;
    }
 
    int Maxflow()
    {
        ;
        while(BFS())
        {
            memset(cur,,sizeof(cur));
            flow += DFS(s,INF);
        }
        return flow;
    }
}DC;
 
bool OK(int Upper)
{
    ;
    DC.init(N+, , N);
    ; i<=C; i++)
        DC.AddEdge(, K+i, );
    ; i<=K; i++)
        DC.AddEdge(i, N, M);
    ; i<=K+C; i++)
        ; j<=K; j++)
            if(Dist[i][j] <= Upper)
                DC.AddEdge(i, j, INF);
    return (DC.Maxflow() == C);
}
 
int main(void)
{
    while(~scanf("%d %d %d", &K, &C, &M)){
 
        ; i<=K+C; i++)
            ; j<=K+C; j++){
                scanf("%d", &Dist[i][j]);
                )
                    Dist[i][j] = INF;
            }
 
//        for(int i=1; i<=K+C; i++){
//            for(int j=1; j<=K+C; j++){
//                printf("%d ", Dist[i][j]);
//            }puts("");
//        }puts("");
 
        ; k<=K+C; k++)
            ; i<=K+C; i++)
                ; j<=K+C; j++)
                    Dist[i][j] = min(Dist[i][j], Dist[i][k]+Dist[k][j]);
 
//        for(int i=1; i<=K+C; i++){
//            for(int j=1; j<=K+C; j++){
//                printf("%d ", Dist[i][j]);
//            }puts("");
//        }puts("");
 
        , FLOOR = INF;
        ; i<=K+C; i++)
            ; j<=K+C; j++){
                if(i==j) continue;
                if(Dist[i][j] == INF) continue;
                UPPER = max(UPPER, Dist[i][j]);
                FLOOR = min(FLOOR, Dist[i][j]);
            }
 
        , mid;
        while(L <= R){
            mid = L + ((R-L)>>);
            ;
            ;
        }
 
        printf("%d\n", ans);
    }
    ;
}

瞎 : 之前是做过 POJ 2391 的，在思考这道题的时候大部分都能想出来，但是在具体实现的时候由于对此类解法的理解不够深厚，在写二分判断函数建边的时候我的代码如下

bool OK(int Upper)
{
    ;
    DC.init(N+, , N);
    ; i<=C; i++)
        DC.AddEdge(, K+i, );
    ; i<=K; i++)
        DC.AddEdge(i, N, M);
    ; i<=K+C; i++) ///这里我傻逼了......
        ; j<=K+C; j++)
            if(Dist[i][j] <= Upper)
                DC.AddEdge(i, j, INF);
    return (DC.Maxflow() == C);
}

当时是理解为从源点出发，然后所有的边去和当前二分答案判断是否加上这一条边，这样牛与牛、机器与机器可能就会连上，因为牛可以通过去其他牛所在的地方去其他机器或者通过其他机器所在的点去另外的机器，也许更优！其实很傻逼......，我没有理解深刻，实际上让原本的矩阵去跑 Floyd 就是做这个事情的，所以跑完 Floyd 之后直接将我们让想要的牛与机器之间最短花费与二分花费去判断，最后连成的是一个二分图。如果按我错误的做法那么跑 Floyd 便失去了意义，多连上了牛和牛的或者机器和机器的那么就有可能使得有些不符合条件的边也被连上！下面举个例子：

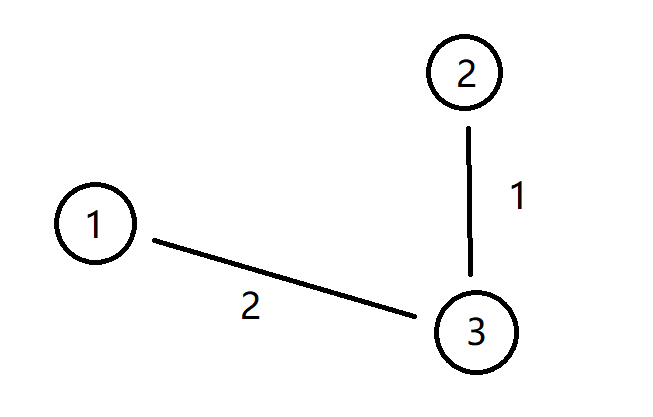
假设 ① 是机器且可接纳两头牛，②、③ 都是牛，假设当前二分的花费为 2

如果按我的错误做法实际 ①、② 之间的最小距离为 3 应该不可达，而①、③可以

但是由于我全局地去连边即我会去判断②、③之间是否花费小于当前二分出来的 2

此时会发现②和③的边被连上了，如果这样去跑最大流会被判定为满流，但是实际不是

所以正确做法是跑完 Floyd 之后只考虑牛和机器就行了

让我意识到这一点的是下面这个例子，建议把图画出来，然后AC代码跑出了我认为不可能跑出的3

下面的例子则是我特意将牛和机器之间的距离放大，然后将一组牛牛距离变小

因为我认为正确代码它只考虑了牛和机器，所以不对，但是事实你也看到了，我傻逼了

2 3 3

0      0     2     0       2

0      0     0   100     0

2      0     0     1       0

0    100   1     0       0

2      0     0     0       0

ans = 3