题解 CF830D Singer House

\(\texttt{Solution}\)

首先考虑 \(\texttt{dp}\) 维护题目要求的深度为 \(i\), 每个节点最多经过一次的不同有向路径数量 \(f_i\)。

明显的，只维护这个东西是不对的，因为忽视了这样的情况：

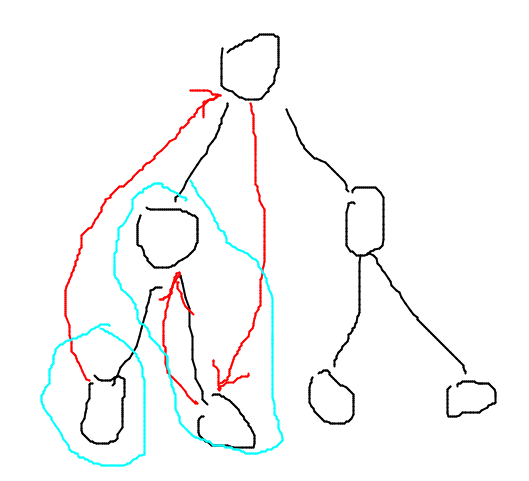
这样子这条路径是由原来的被蓝色圈圈包住的两个部分转移而来。

那么考虑记录 \(g_i\) 为两条不相交的有向路径数量。

然后蒟蒻兴冲冲地去 尝试了, 并过了前两个样例，但是过不了第三个样例，这是为什么？

发现 \(g_i\) 也有可能是由三条不相交的有向路径转移而来！

那么正解就浮出水面了：维护深度为 \(i\), \(j\) 条不相交的有向路径数量 \(dp_{i,j}\)。

转移如果想明白了状态其实很简单。这里还是说一下。

首先用背包求出深度为 \(i-1\), 和为 \(j\) 条不相交的有向路径数量 : bb[j] += dp[i - 1][k] * dp[i - 1][j - k]

第一种转移：根结点独立，然后其他的路径让两个子树自由组合 : dp[i][j] += bb[j - 1] + 2 * dp[i - 1][j - 1]

第二种转移：路径不包括根结点，或根结点为路径起点或终点： dp[i][j] += (2 * j + 1) * bb[j] + (4 * j + 2) * dp[i - 1][j]

第三种转移：路径包括根结点，且连接两条原来在子树中是两条链： dp[i][j] += j * (j + 1) * bb[j + 1] + 2 * j * (j + 1) * dp[i - 1][j + 1]

\(\texttt{Code}\)

#include<bits/stdc++.h>
#define L(i, j, k) for(int i = j; i <= k; i++)
#define R(i, j, k) for(int i = j; i >= k; i--)
using namespace std;
const int N = 444;
const int mod = 1e9 + 7;
int n, dp[N][N], bb[N];
int main() {
    scanf("%d", &n);
    dp[1][1] = 1;
    L(i, 2, n) {
        fill(bb, bb + n + 1, 0);
        L(j, 1, n) L(k, 0, j) (bb[j] += 1ll * dp[i - 1][k] * dp[i - 1][j - k] % mod) %= mod;
        dp[i][1] = 1;
        L(j, 1, n) {
            int t = 0;
            (dp[i][j] += (2ll * j + 1) * bb[j] % mod) %= mod;
            (dp[i][j] += (4ll * j + 2) % mod * dp[i - 1][j] % mod) %= mod;
            (dp[i][j] += 1ll * j * (j + 1) % mod * bb[j + 1] % mod) %= mod;
            (dp[i][j] += 2ll * j * (j + 1) % mod * dp[i - 1][j + 1] % mod) %= mod;
            (dp[i][j] += bb[j - 1] % mod) %= mod;
            (dp[i][j] += 2ll * dp[i - 1][j - 1] % mod) %= mod;
        }
    }
    printf("%d\n", dp[n][1]);
    return 0;
}