Codeforces Edu Round 64 A-D

A. Inscribed Figures

分类讨论打表即可。

PS：这道题翻译有歧义。

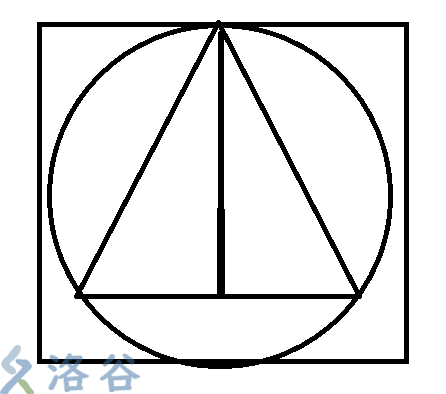
这样稍微翻转一下，就可以是\(7\)个交点呀...（大概是我没看英文题干导致的惨案）

#include <cstdio>
#include <iostream>
using namespace std;
const int N = 110;
int n, a[N], ans = 0;
int d[3][3]{
	{-1, 3, 4},
	{3, -1, -1},
	{4, -1, -1}
};
int main(){
	scanf("%d", &n);
	for(int i = 1; i <= n; i++)
		scanf("%d", a + i);

	for(int i = 2; i <= n; i++){
		int res = d[a[i - 1] - 1][a[i] - 1];
		if(i > 1 && i + 1 <= n && a[i + 1] == 2 && a[i] == 1 && a[i - 1] == 3) res = 3;
		if(res == -1){
			puts("Infinite");
			return 0;
		}else{
			ans += res;
		}
	}
	printf("Finite\n%d\n", ans);
	return 0;
}

B. Ugly Pairs

将奇数字母\((char - 'a') \& 1\)与偶数字母分别分开来升序排序，设为\(A\)、\(B\)。

尝试\(AB\)或者\(BA\)，若都不行则无解（注意，题有坑，\(za\)是可以的，而\(az\)不行）

---

证明：

\(A\)与\(B\)都满足\(str[i] <= str[i + 1] (1 <= i < len)\)

若\(A.end()\)不满足\(B.begin()\)，反过来匹配也不行。则说明无论怎么拼，它们都是不严谨递增的。

则它们的开头与结尾是相邻的，它们相当于一个并行的状态，必须有一方是不严谨递增的重复字母且一方邻向。（否则不可能不严谨递增）

#include <cstdio>
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
char s[N];
int n, vis[N];
vector<char> A, B;
char inline pre(char c){
	return 'a' + ((c - 'a' + 25) % 26);
}
char inline nxt(char c){
	if(c == 'z') return '?';
	return 'a' + ((c - 'a' + 1) % 26);
}
int main(){

	int T; scanf("%d", &T);
	while(T--){
		A.clear(); B.clear();
		scanf("%s", s + 1);
		n = strlen(s + 1);
		for(int i = 1; i <= n; i++){
			if((s[i] - 'a') & 1) A.push_back(s[i]);
			else B.push_back(s[i]);
		}
		sort(A.begin(), A.end());
		sort(B.begin(), B.end());
		if(A.empty() || B.empty()){
			for(int i = 0; i < A.size(); i++)
				putchar(A[i]);
			for(int i = 0; i < B.size(); i++)
				putchar(B[i]);
			printf("\n");
		}else if(pre(A.back()) != B[0] && nxt(A.back()) != B[0]){
			for(int i = 0; i < A.size(); i++)
				putchar(A[i]);
			for(int i = 0; i < B.size(); i++)
				putchar(B[i]);
			printf("\n");
		}else if(pre(B.back()) != A[0] && nxt(B.back()) != A[0]){
			for(int i = 0; i < B.size(); i++)
				putchar(B[i]);
			for(int i = 0; i < A.size(); i++)
				putchar(A[i]);
			printf("\n");
		}else puts("No answer");
	}
	return 0;
}

C. Match Points

发现答案具有单调性，既然有\(3\)个，那么一定有\(2\)对，可以二分答案。

\(check()\)函数的检查是一个贪心的过程，使\(x_i\)匹配\(x_{(n / 2) + i}\)这样是很明显最优的方案。

---

证明：

存在\(x_a <= x_b <= x_c <= x_d\)

若\((a, b),(c, d)\) 可匹配成功，那么\((a, c),(b, d)\)必定能匹配成功，反命题则不然。

那么\(x_b - x_a >= z\)，也就是\(x_c >= x_b >= z + x_a\)，换过来就是\(x_c - x_a >= z\)

\((b, d)\)的证明同理，所以一一匹配一定是最优的。

PS：写完了程序才发现可以直接\(O(n)\)求解，看了题解才知道自己太弱了...

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 200010;
int n, z, x[N];
bool check(int m){
	for(int i = 1; i <= m; i++)
		if(x[n - m + i] - x[i] < z) return false;
	return true;
}
int main(){
	scanf("%d%d", &n, &z);
	for(int i = 1; i <= n; i++)
		scanf("%d", x + i);
	sort(x + 1, x + 1 + n);
	int l = 0, r = n / 2;
	while(l < r){
		int mid = (l + r + 1) >> 1;
		if(check(mid)) l = mid;
		else r = mid - 1;
	}
	printf("%d\n", l);
	return 0;
}

D. 0-1-Tree

自闭，想不到什么好方法，\(dp\)死活想不出来...

计数问题，可以利用加法原理分开处理。

符合条件的点对\((u, v)\)有三种情况：

1. 全部是\(0\)边
2. 全部是\(1\)边
3. 先经过一些\(0\)边，然后经过\(1\)边

对于情况\(1\)，我们可以考虑让图仅存在\(0\)边，然后对于每个连通块，它的点对数量为：

\(size * (size - 1)\)。可以理解为每一个点可以找另外连通块的所有点，交换下来仍然成立。

对于情况\(2\)，同理情况\(2\)。

对于情况\(3\)，可以考虑找到一个截点\(x\)，路径考虑为\(s -> x -> t\)，\(s - > x\)上的路径全部为\(0\)，\(x -> t\)的路径全部为\(1\)。这种情况，方案数为\((size_{x属于的0边连通块} - 1) * (size_{x属于的1边连通块} - 1)\)，理解为在\(x\)属于的\(0\)边连通块中找一个点\(s(s != x)\) ，在\(1\)边同理。

对于上述所有操作，仅仅是集合之间的合并，可以用并查集维护。

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long LL;
const int N = 200010, M = N << 1;
int n, f[N][2], size[N][2];
LL ans = 0;
int inline find(int x, int c){
    return f[x][c] == x ? x : f[x][c] = find(f[x][c], c);
}
void merge(int a, int b, int c){
    a = find(a, c), b = find(b, c);
    if(a != b) f[a][c] = b, size[b][c] += size[a][c];
}
int main(){
    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        f[i][0] = f[i][1] = i;
        size[i][0] = size[i][1] = 1;
    }
    for(int i = 1, u, v, w; i < n; i++){
        scanf("%d%d%d", &u, &v, &w);
        merge(u, v, w);
    }

    for(int i = 1; i <= n; i++){
        if(f[i][0] == i)
            ans += (LL)size[i][0] * (size[i][0] - 1);
        if(f[i][1] == i)
            ans += (LL)size[i][1] * (size[i][1] - 1);
        int p = find(i, 0), q = find(i, 1);
        ans +=  (LL)(size[p][0] - 1) * (size[q][1] - 1);
    }
    printf("%lld\n", ans);
    return 0;
}