lca讲解 && 例题 HDU - 4547

一、

最普通的找树中两个点x，y最近公共祖先：

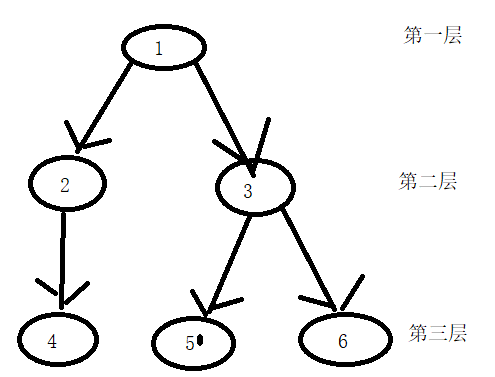
在进行lca之前我们要先对这一颗树中的每一个点进行一个编号,像下图一样。这个编号就是tarjan算法中的dfn[]数组

这样的话我们可以在跑tarjan算法的时候可以记录一下每一个点的父亲节点，例如pre[5]=pre[6]=3

前提条件都有了，我们就可以让dfn值更大的那一个点x(这里假设dfn[x]>dfn[y])每一次跳到他的父亲节点。一直跳到dfn[x]<dfn[y]，就可以结束了。然后就是判断一下dfn[x]是否等于dfn[y],如果等于就找到了最近公共祖先，否则就让y点往它父亲节点上一次一次跳。这样他们一定会遇到dfn[]相等的时候。

因为这个dfn[]数组里面的编号是dfs过程中一次一次的加一。所以我们再x往父亲节点上面跳的过程中如果dfn[x]<dfn[y]那么这个x点肯定是dfs过程中比y先遍历到的点。这一点可以想一下！

例如：找上面那个图中编号为6和3的公共祖先，那么dfn值大的点先跳，那么6跳到1的时候才会结束循环。而显然这个1也是3的祖先

代码：

 1 int lca(int u,int v)  //找到公共最近父节点
 2 {
 3     int res=0;
 4     if(dfn[u]<dfn[v]) swap(u,v);
 5     while(dfn[u]>dfn[v])
 6     {
 7         res++;
 8         u=pre[u];  //pre是u父亲节点
 9     }
10     while(dfn[v]>dfn[u])
11     {
12         res++;
13         v=pre[v];
14     }
15     //经过上面两个while，这样dfn[u]==dfn[v]此时他们就到达了最近公共父节点
16     return v;
17 }

二、

另一种普通找树两点x，y最近公共祖先：

先对树进行分层，并记录一下每一个点的父亲节点

 1 //pre表示每个点的父节点，depth表示每个点的深度
 2
 3 int pre[100],depth[100]; //越靠近树根深度越浅，否则越深
 4
 5 int lca(int u,int v)
 6
 7 {
 8
 9     //在函数中确保u的深度大于v的深度，方便后面操作。
10
11     if(depth[u]<depth[v])
12
13         swap(u,v);
14
15     //让v不断地跳到他的父节点上，直到与u的深度相同
16
17     while(depth[u]>depth[v])
18
19         u=pre[u];
20
21     //让u和v同时往上跳，直到两者相遇。
22
23     while(u!=v)
24
25     {
26
27         u=pre[u];
28
29         v=pre[v];
30
31     }
32     //因为上一个while循环已经使他们处于同一层，但是在同一层还是有可能不是一个点，所以要一直跳到
33     //u==v才可以
34     return u;
35
36 }

比如找2和5的最近公共祖先，那么肯定是5深度更深，那么5首先跳到3。这个时候2和3在同一层，但是它们不相等也就不会是2和5的最近公共祖先。这个时候要两个点一起往上跳到上一层1.此时就找到了

三、

参考链接：https://blog.csdn.net/Q_M_X_D_D_/article/details/89924963

倍增法优化lca(这一中方法是对第二种方法的优化)：

上面的方法都是一层一层地往上跳，效率太低了。我们可以一次多往上面跳几层。假设两点x和y的层数之差是d

那么d肯定可以由(2^1)、(2^2)、(2^3)、(2^4)、(2^5)......(2^i)(2的次幂)组成。而且d的二进制模式正好对应着一个(2^i)。这个时候d的二进制中有几个1，那么只需要跳几次。比之前跳的次数大大减少

上面的进行完之后我们可以保证x、y已经在同一层上了。然后就是判断它们需要往上面跳几次才能变为同一个点

我们知道如果c是a和b的LCA，那么c的所有祖先同样也是a和b的公共祖先，但不是最近的。

利用这一点我们可以从最远的开始跳(意思就是跳的层数从大到小枚举)，这样的话如果跳到那一层之后两点还不相等我们就跳。这样跳到最后我们所在的层数的上一层就是两点的最近公共祖先。

但是随之而来的新问题是：怎么知道我跳了8层之后到达了哪个结点？下面就要用ST算法来解决这个问题：

 1 ST算法：
 2 是解决RMQ（区间最值）问题，它能在O（nlogn）的时间预处理，然后O（1）回答。
 3 其原理是倍增，f[i][j]表示从i位起的2^j个数中的最大数，即[i,i+2^j-1]中的最大值
 4
 5 f[i][0]表示[i,i]中的最大值，只能是a[i]，故f[i][0]=a[i]。对于任意的f[j][i]，
 6 我们分成两段相等长度的数列来看，[j,j+2^(i-1)-1]和[j+2^(i-1),j+2^i-1]，
 7 分别对应f[j][i-1]和f[j+(1<<i-1)][i-1]。既然这两段的最大值都知道了，
 8 它们又恰好完全地覆盖了[j,j+2^i-1]，它俩的最大值就是这个区间的最大值。
 9
10 lca版ST：
11
12 所以我们定义倍增法中的DP[i][j]为：结点 i 的向上 2^j 层的祖先。
13
14 DP[i][j] = DP[ DP[i][j-1] ] [j-1]。
15 如何理解这个递推式呢？DP[i][j-1]是结点i往上跳2^(j-1)层的祖先，
16 那我们就在跳到这个结点的基础上，再向上跳2^(j-1)层，这样就相当于从结点i，
17 先跳2^(j-1)层，再跳2^(j-1)层，最后还是到达了2^j层。

在给树分层的时候顺便把dp[i][0],即i点的父亲节点处理一下，然后dp把数组中每一个位置的值都求出来

 1 void DP(int n)
 2 {
 3     for(int j=1;(1<<j)<=n;++j)
 4     {
 5         for(int i=1;i<=n;++i)
 6         {
 7             dp[i][j]=dp[dp[i][j-1]][j-1];
 8         }
 9     }
10 }

之后就是lca查询过程：

 1 int lca(int x,int y)  //dfn里面放的是层数
 2 {
 3     if(dfn[x]<dfn[y]) swap(x,y);
 4     int d=dfn[x]-dfn[y];
 5     for(int i=0;i<M;++i)  //使x和y处于同一层
 6     {
 7         if((1<<i)&d)
 8             x=dp[x][i];
 9     }
10
11     if(x==y) return x;   //相等就返回
12     for(int i=M-1;i>=0;i--)  //不相等就一起往上面跳，但是不能跳过
13     {  //例如距离x、y7层才是它们的公共祖先，当你直接跳8层就会跳过，这个时候你就可以4、2、1去跳到
14         if(dp[x][i]!=dp[y][i])  //它们最近公共祖先的下一层
15         {
16             x=dp[x][i];
17             y=dp[y][i];
18         }
19     }
20     return dp[x][0];  //最后返回的时候因为我们得到的就是最近公共祖先的下一层，所以要得到最近公共祖先，就要返回他的上一级
21 }

例题：

在Windows下我们可以通过cmd运行DOS的部分功能，其中CD是一条很有意思的命令，通过CD操作，我们可以改变当前目录。
　　这里我们简化一下问题，假设只有一个根目录，CD操作也只有两种方式：

　　

　　1. CD 当前目录名\...\目标目录名 (中间可以包含若干目录，保证目标目录通过绝对路径可达)

　　2. CD .. (返回当前目录的上级目录)

　　

　　现在给出当前目录和一个目标目录，请问最少需要几次CD操作才能将当前目录变成目标目录？

Input输入数据第一行包含一个整数T(T<=20)，表示样例个数；

每个样例首先一行是两个整数N和M(1<=N,M<=100000)，表示有N个目录和M个询问；

接下来N-1行每行两个目录名A B(目录名是只含有数字或字母，长度小于40的字符串)，表示A的父目录是B。

最后M行每行两个目录名A B，表示询问将当前目录从A变成B最少要多少次CD操作。

数据保证合法，一定存在一个根目录，每个目录都能从根目录访问到。Output请输出每次询问的结果，每个查询的输出占一行。Sample Input

2
3 1
B A
C A
B C

3 2
B A
C B
A C
C A

Sample Output

2
1
2

题解：

从子节点往父节点跳，每跳一次就让最后结果加1，如果从父节点往它的子节点跳，无论跳多远只加1

题解：

先用map给每一个字符串一个映射值。然后用一下lca。

1、如果x、y的lca是x，那么输出1

2、如果x、y的lca是y，那么输出x，y的层数之差

3、如果x、y相等，输出0

4、如果x、y的lca既不是x也不是y，那就让lca的层数减去x的层数，然后加1。因为从x到lca那一层需要可能许多次，但是x已经到了lca那一层之后y就已经是它的子节点了，那个时候从x到y只需要一次

代码：

  1 #include<stdio.h>
  2 #include<string.h>
  3 #include<iostream>
  4 #include<algorithm>
  5 #include<map>
  6 using namespace std;
  7 const int maxn=100005;
  8 const int M=20;
  9 int v[maxn],head[maxn],cnt,visit[maxn],dfn[maxn],pre[maxn];
 10 int dp[maxn][M];
 11 map<string,int>r;
 12 struct edge
 13 {
 14     int v,next;
 15 }e[maxn<<1];
 16 void add_edge(int x,int y)
 17 {
 18     e[cnt].v=y;
 19     e[cnt].next=head[x];
 20     head[x]=cnt++;
 21 }
 22 void dfs(int x,int ci)
 23 {
 24     //dp[x][0]=x;
 25     visit[x]=1;
 26     dfn[x]=ci;
 27     for(int i=head[x];i!=-1;i=e[i].next)
 28     {
 29         int to=e[i].v;
 30         if(!visit[to])
 31         {
 32             dp[to][0]=x;
 33             pre[to]=x;
 34             dfs(to,ci+1);
 35         }
 36     }
 37 }
 38 void DP(int n)
 39 {
 40     for(int j=1;(1<<j)<=n;++j)
 41     {
 42         for(int i=1;i<=n;++i)
 43         {
 44             dp[i][j]=dp[dp[i][j-1]][j-1];
 45         }
 46     }
 47 }
 48 int lca(int x,int y)
 49 {
 50     if(dfn[x]<dfn[y]) swap(x,y);
 51     int d=dfn[x]-dfn[y];
 52     for(int i=0;i<M;++i)
 53     {
 54         if((1<<i)&d)
 55             x=dp[x][i];
 56     }
 57
 58     if(x==y) return x;
 59     for(int i=M-1;i>=0;i--)
 60     {
 61         if(dp[x][i]!=dp[y][i])
 62         {
 63             x=dp[x][i];
 64             y=dp[y][i];
 65         }
 66     }
 67     return dp[x][0];
 68 }
 69 void init(int n)
 70 {
 71     memset(dp,0,sizeof(dp));
 72     for(int i=1;i<=n;++i)
 73     {
 74         visit[i]=dfn[i]=0;
 75         head[i]=-1;
 76     }
 77     cnt=0;
 78 }
 79 int main()
 80 {
 81     int t;
 82     scanf("%d",&t);
 83     while(t--)
 84     {
 85
 86         int n,m,index=0,pos,nn;
 87         string x,y;
 88         scanf("%d%d",&n,&m);
 89         init(n);
 90         nn=n;
 91         for(int i=1;i<=n;++i)
 92             v[i]=i;
 93         while(--nn)
 94         {
 95             cin>>x>>y;
 96             if(r[x]==0) r[x]=++index;
 97             if(r[y]==0) r[y]=++index;
 98             v[r[x]]=r[y];
 99
100             add_edge(r[x],r[y]);
101             add_edge(r[y],r[x]);
102         }
103         for(int i=1;i<=n;++i)
104         {
105             if(v[i]==i) pos=i;
106         }
107         dfs(pos,1);
108         DP(n);
109         int res;
110         while(m--)
111         {
112             cin>>x>>y;
113             int ans=lca(r[x],r[y]);
114             if(r[x]==r[y]) res=0;
115             else if(ans==r[x])
116                 res=1;
117             else if(ans==r[y])
118                 res=dfn[r[x]]-dfn[ans];
119             else res=dfn[r[x]]-dfn[ans]+1;
120             printf("%d\n",res);
121         }
122         r.clear();
123     }
124     return 0;
125 }