【Notes】现代图形学入门_01

跟着闫令琪老师的课程学习，总结自己学习到的知识点

课程网址GAMES101

B站课程地址GAMES101

课程资料百度网盘【提取码：0000】

计算机图形学概述

计算机图形学是一门将模型转化到屏幕上图像的一门基础学科，主要分为：Rasterization(光栅化)、Curves and Meshes(几何表示)、Ray Trancing(光线追踪)、Animation/Simulation(动画和模拟)

图形学与计算机视觉的简单界限：

(1) 计算机视觉是将屏幕上的图片转化为模型的过程;

(2) 计算机图形学是一门将模型转化到屏幕上图像的一门基础学科。

每个类别的知识框架如下图：

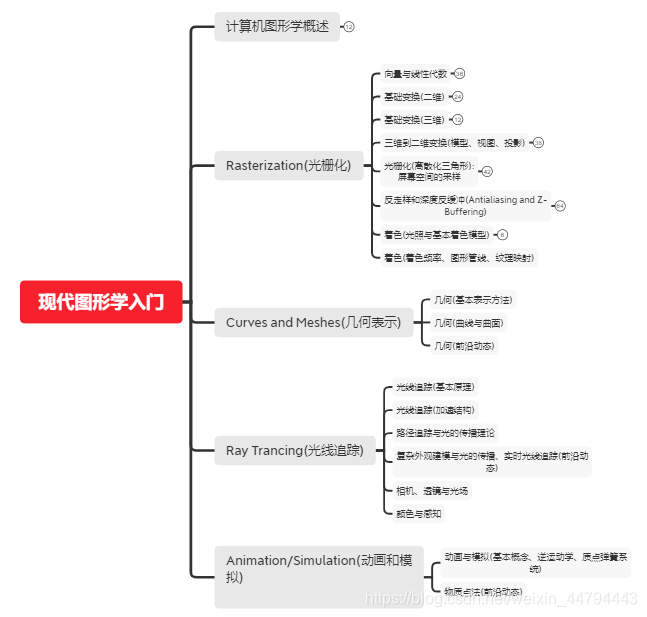
Rasterization(光栅化)

点乘和叉乘

Dot Multiplication

点乘在图形学的应用

(1) 求两个向量之间的夹角:

$$\cos(\theta) = \frac{(\vec{a} \cdot \vec{b})}{\lVert a \lVert \lVert b \lVert}$$

可以判断两个向量的距离、分向量与判断向量前后



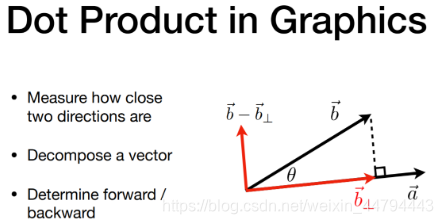
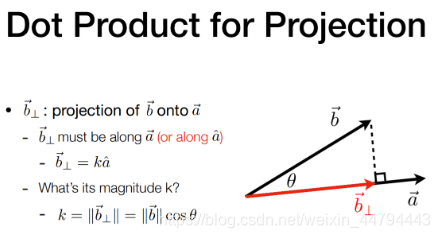
(2) 投影

一个向量在另一个向量上的投影

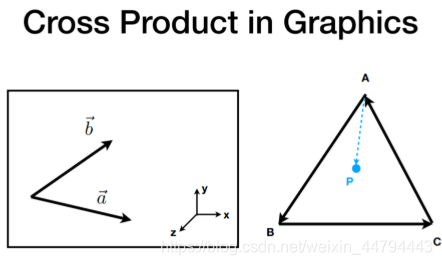
Cross Product

[1] 右手坐标系



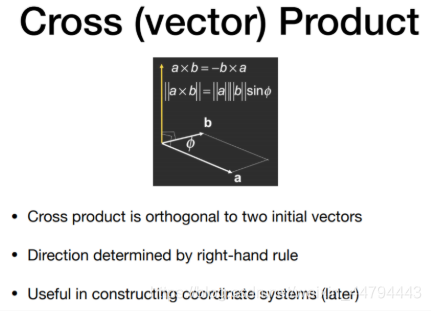
右手坐标系

叉乘在图形学中的应用

(1) 判断一个向量在另一个向量的左右，叉乘为正(与右手方向一致)，则为目标在自己右方，反之亦然；

(2) 在性质(1)的基础上，如果一个点在包围他的所有线的同一侧，那么可以说明该点在这个图形内，反之亦然。

矩阵

矩阵转置与逆

(1) 矩阵A、B乘积的转置等于B的转置矩阵乘A的转置矩阵

\[(AB)^T=B^TA^T
\]

(2) 矩阵AB的逆等于B的逆乘A的逆

\[(AB)^{-1} = B^{-1}A^{-1}
\]

基础变换(二维)

三维变化与二维变换矩阵类似

齐次坐标下的基础变换

Scale:

\[S(s_x,s_y) =\begin{pmatrix}
s_x &0 &0\\
0 & s_y & 0 \\
0&0&1
\end{pmatrix}\]

Rotation:

\[R(\alpha) = \begin{pmatrix}
\cos\alpha& - \sin\alpha & 0 \\
\sin\alpha & \cos \alpha &0 \\
0&0&1
\end{pmatrix}\]

Translation:

\[T(t_x,t_y)=\begin{pmatrix}
1 & 0 & t_x \\
0 &1& t_y\\
0 &0& 1
\end{pmatrix}\]

组合变换(Compositon Transform)

矩阵变换把先变化的矩阵放到右边：矩阵运算是从右向左

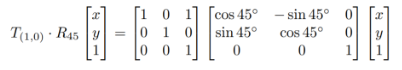
四元数与旋转公式

四元数

留个坑，下周再填

罗德里格斯旋转公式

Rodrigue's Rotation Formula: Raotation by angle \(\alpha\) around axis \(\vec{n}\)

\[R(\vec{n},\alpha)=cos(\alpha)I+(1-cos(\alpha))nn^{T}+\sin(\alpha)
\begin{matrix} \underbrace{
\begin{pmatrix}
0 & -n_z & n_y \\
n_z & 0 & -n_x \\
-n_y & n_x & 0
\end{pmatrix}
} \\ N\end{matrix}\]

In the formula

I ：Identity matrix

最后乘积的结果是一个3*3的矩阵

MVP变换

Model Transformation

引用博客：MVP变换

对模型进行模型变换时，需要注意坐标系是在世界坐标系原点。当绕模型中心进行变换时，首先要将模型的中心点移动到世界坐标系的原点，之后在进行模型变换，之后移回到原来的位置。

矩阵描述为：$$M=M_t^{-1} M_r M_s M_t$$

View/Camera Transformation

这个过程是将确定相机的位置：将相机的位置通过下面的过程移动到固定的点和方向。

(1) 相机的位置固定在世界坐标系的原点： \(\vec{e}\)

(2) 相机的朝向 \(-\vec{Z}\)： \(\hat{g}\)

(3) 相机的向上方向\(\vec Y\)： \(\hat t\)

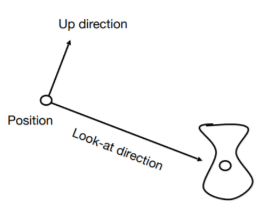
基于上述过程，要求视图变换矩阵\(M_{view}\)分别求相机的平移矩阵\(T_{view}\)、旋转矩阵\(R_{view}\)

\[T_{view} = \begin{bmatrix}
1 & 0 & 0 & -x_{\vec{e}} \\
0 & 1 & 0 & -y_{\vec{e}} \\
0 & 0 & 1 & -z_{\vec{e}} \\
0 & 0 & 0 & 1
\end{bmatrix}\]

求旋转矩阵时，直接求相机旋转到原点的矩阵不容易求解，但求原点到相机位置的旋转矩阵容易求。

所以先求原点到相机的旋转矩阵：Z To \(-\hat{g}\)、Y To \(\hat{t}\)、最后保证\(\vec{X}\) To \((\hat g \times \hat t)\) 朝向的方向，原因是保证符合右手坐标系。

\[R_{view}^{-1}=\begin{bmatrix}
x_{\hat{g} \times \hat{t}}&x_{t}&x_{-g}&0\\
y_{\hat{g} \times \hat{t}}&x_{t}&y_{-g}&0\\
z_{\hat{g} \times \hat{t}}&x_{t}&z_{-g}&0\\
0&0&0&1
\end{bmatrix}\]

因为\(R_{view}^{-1}\)是正交矩阵，所以逆矩阵和旋转矩阵相同。

\[R_{view} =\begin{bmatrix}
x_{\hat{g} \times \hat{t}}&y_{\hat{g} \times \hat{t}}&z_{\hat{g} \times \hat{t}}&0\\
x_{t}&y_{t}&z_{t}&0\\
x_{-g}&y_{-g}&z_{-g}&0\\
0&0&0&1
\end{bmatrix}\]

所以

\[M_{view} = R_{view} T_{view}=
\begin{bmatrix}
x_{\hat{g} \times \hat{t}}&y_{\hat{g} \times \hat{t}}&z_{\hat{g} \times \hat{t}}&0\\
x_{t}&y_{t}&z_{t}&0\\
x_{-g}&y_{-g}&z_{-g}&0\\
0&0&0&1
\end{bmatrix}

\begin{bmatrix}
1 & 0 & 0 & -x_{\vec{e}} \\
0 & 1 & 0 & -y_{\vec{e}} \\
0 & 0 & 1 & -z_{\vec{e}} \\
0 & 0 & 0 & 1
\end{bmatrix}\]

Projection Transformation

个人理解投影变换的终极目的是让物体挤压在一个单位大小的平面(空间)内。原因先挖个坑。

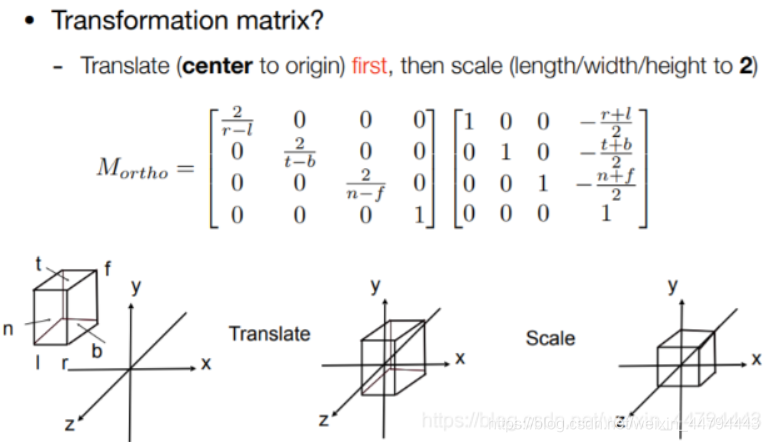
Orthographic Projection

简单理解就是将物体的忽略z坐标，将模型通过Scale To [-1,-1]^2平面内。

真正的操作：

(1) 移动模型的位置到原点

(2) 缩放模型到空间[-1,1]^3中

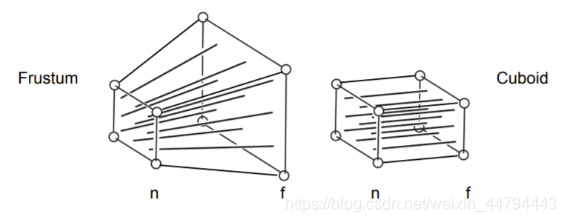
Perspective Projection

正视投影的光线可以看成是一个立方体，如上图。透视投影的光线可以看成一个视锥，如下图。

透视变换可以分为两个步骤进行：

(1) 将视锥挤压到立方体内\(M_{persp->ortho}\)

(2) 将挤压后的视锥进行正视投影变换$M_{ortho}

挤压时的变换矩阵\(M_{persp->ortho}=\begin{bmatrix}
n&0&0&0\\
0&n&0&0\\
0&0&n+f&-nf\\
0 & 0&1&0
\end{bmatrix}\)

所以投影变换矩阵

\[M_{proj}=M_{ortho}M_{persp->ortho}
\]

光栅化

Viewport Transform（视口变换）

将经过MVP变换后得到的单位空间模型变换到屏幕上，屏幕左边是左下角为原点。



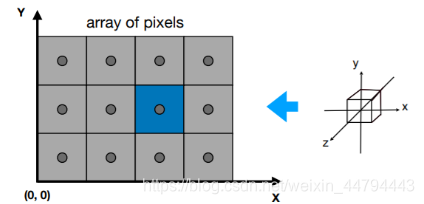
所以视口变换的矩阵

\[M_{viewport}=\begin{pmatrix}
\frac{width}{2}&0&0&\frac{width}{2}\\
0& \frac{height}{2}&0&\frac{height}{2}\\
0&0&1&0\\
0&0&0&1
\end{pmatrix}\]

Rasterization:Draw to Raster Displays

主要是将已经经过视口变换的模型画在屏幕空间上。

主要过程有：

(1) 采样

(2) 判断像素中心的位置与三角形的关系

采样

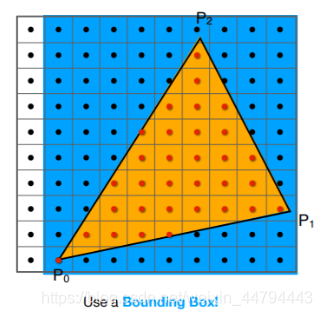
因为屏幕空间本身分辨率已经给出，所以像素点的数量也已经确认了，但是对我们可以通过以下方法提高效率，将可能有用的像素点选取出来：

1.Bounding Box

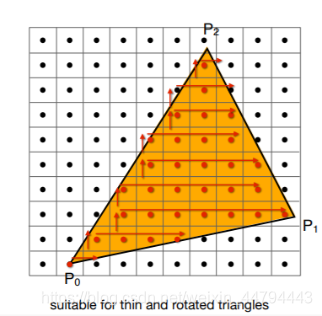
2.Incremental Triangle Traversal

判断像素中心的位置与三角形的关系

主要应用的原理是利用向量的叉乘判断点是否在三角形内。

伪代码如下

for(int x =0 ;x<xmax;x++)
	for(int y = 0;y<ymax;y++)
		image[x][y]=inside(tri,x+0.5,y+0.5)

反走样与深度缓冲

Artifacts(瑕疵) in Computer Graphics

产生Artifacts的分类和原因

(1) Jaggies(Staircase Pattern)

原因：空间采样产生的锯齿

(2) Mpire

原因：图片欠采样

(3) Wagon Wheel Effect

原因：时间上采样产生

解决办法

(1) 提高采样率：不实用

(2) 反走样

反走样

反锯齿的思路是先模糊，后采样，顺序不可以调换。

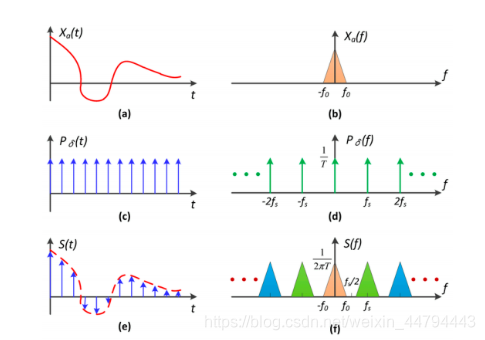
走样的原因：采样频率满足奈奎斯特采样定律，即采样频率高于二倍的最高频率。

滤波

频率图：越靠近中心点，表示的频率越低

滤波器的种类大致分为四类:

(1) 低通滤波：应用的效果是模糊

(2) 高通滤波：应用效果是提取边缘信息

(3) 带通滤波：也可以绘制出图像的边缘信息

卷积定理

时域卷积、频域相乘

时域卷积，频率图向两边拓展。

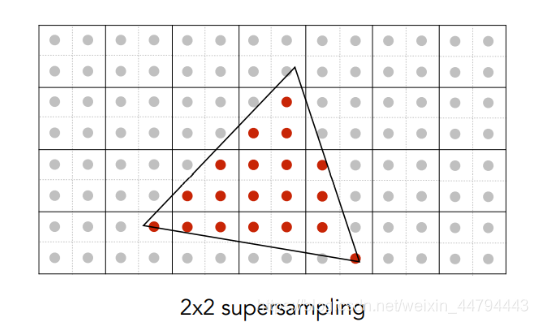
MSAA

通过MSAA方法可以首先模糊的效果。

步骤如下：

(1) 将每个像素点再进行细分

(2) 判断一个像素点里有几个细分的点在三角形内

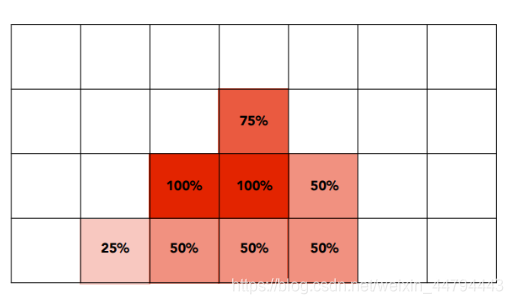
(3) 将像素点根据在三角星内部细分点不同程度的着色，表示已经模糊。

上述过程的流程图如下：





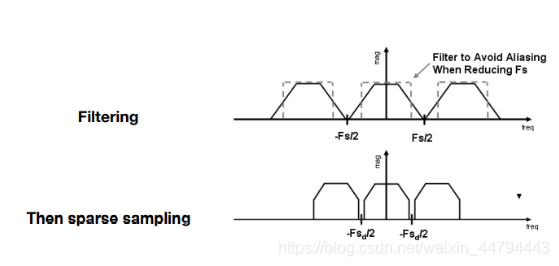
上述过程在频率上的过程相当于低通滤波

Z-Buffer深度缓冲

每个像素都有一个z值代表像素点的深度、z值越大，说明该点越远。

Z-Buffer 算法伪代码

Initalize depth buffer to \(\infty\)

for(each trangle T)
	for(each sample(x,y,z) in T)
		if(z<zbuffer[x,y])   //closeet samnple so far
			zbuffer[x,y]=z;  //update color
			framebuffer[x,y]=rgb;   //update depth

总结

本周主要是完成光栅化的过程。其中比较重要的几个知识点：向量点乘和叉乘的几何意义、齐次坐标系下的矩阵变换、MVP变换、视口变换、光栅化、反走样、Z-Buffrer深度缓冲等等基础概念。